
ゲージ固定は, 計算電磁気学で最も興味深いトピックの1つです. このブログでは, ゲージ固定の概要と背景をご紹介し, COMSOL Multiphysics® ソフトウェアでいつどのように使用するかについてご説明します.
ヘルムホルツの定理
COMSOL Multiphysics® の電磁気フィジックスインターフェースはすべて, いずれもマックスウェル方程式の解を出すことを目的としていますが, それらの違いは何でしょうか? そもそもなぜ複数のマックスウェルインターフェースが必要なのでしょうか?
その質問に答え, いくつかのよくある誤解を解くために, 一歩下がって, ベクトル場の一般的な数学的概念を見てみましょう. マックスウェルの方程式は, 空間と時間の関数であるベクトル場を扱います. つまり, \textbf{E}, \textbf{D}, \textbf{H}, \textbf{B} です.
マックスウェルの方程式を解析するための良い出発点は, ヘルムホルツの定理です (ベクトル計算の基本定理とも呼ばれる). これは, 任意のベクトル場 \textbf{F} をカールのない部分と発散のない部分に分解できることを述べています. また, どこでも \nabla \times \textbf{F} と \nabla \cdot \textbf{F} であることを知ることで, また, トランケートされたドメインについては, 適切な境界条件を知ることで, ベクトル場が一意に決定されることを示しています.
もちろん, \textbf{F} を解析的に表現することは依然として困難または不可能であり, 数値的に計算することも困難かもしれません.
マックスウェル方程式
微分形式のマックスウェル方程式は次のように書かれます.
\begin{align*}
\begin{split}
\nabla \cdot \textbf{D} = \rho, \quad \text{(ガウスの法則 )} \\
\nabla \times \textbf{E} = -\frac{\partial\textbf{B}}{\partial t} , \quad
\text{(ファラデーの法則)} \\
\nabla \cdot \textbf{B} = 0, \quad \text{(磁気ガウスの法則)} \\
\nabla \times \textbf{H} = \textbf{J} + \frac{\partial\textbf{D}}{\partial t} , \quad
\text{(マックスウェル・アンペアの法則)} \\
\end{split}
\end{align*}
\end{equation}
ここで, \textbf{E} と \textbf{H} はそれぞれ電場と磁場の強さ, \textbf{D} と \textbf{B} は, それぞれ電束密度と磁束密度, \rho と \textbf{J} は, それぞれ電荷密度と導電電流密度です.
さらに, 物質法則は, \textbf{E} を \textbf{D} に, \textbf{H} を \textbf{B} に一意に関連付けます. 次に, ヘルムホルツの定理から, これらの方程式は (十分な境界条件とともに), \nabla \times \textbf{E} と \nabla \cdot \textbf{E} の両方が規定され, \nabla \times \textbf{H} と \nabla \cdot \textbf{H} についても同様に, 一意のベクトル場 \textbf{E}, \textbf{D}, \textbf{H}, \textbf{B} を出すことがわかります.
ポテンシャルの導入
マックスウェル方程式をスカラーおよびベクトルのポテンシャルで再定式化すると便利なことがよくあります. これらは必ずしも一意ではなく, 以下でご説明するように, ヘルムホルツの定理を使用して解析する必要があります.
静力学では \nabla \times \textbf{E} = \textbf{0}, 静磁気では電流がない場合は \nabla \times \textbf{H} = \textbf{0} であることがわかります.
つまり, これらの場合, スカラーポテンシャル (任意のスカラー関数 \nabla \times (\nabla f)= \textbf{0} の f として) を使用して, それぞれ \textbf{E} と \textbf{H} を次のように表すことができます.
また, \nabla \cdot \textbf{B} = 0 が常に成立し, 自由電荷がない場合は \nabla \cdot \textbf{D} = 0 が成立することもわかります.
次に, ベクトルポテンシャル (任意のベクトル場 \nabla \cdot (\nabla \times \textbf{F}) = 0 に対して \textbf{F}) を使用して, \textbf{B} と \textbf{D} の発散のない部分 (電荷密度がない場合) をそれぞれ次のように表すことができます.
スカラーポテンシャルを使用すると, 場の成分またはベクトルポテンシャルの直接表現を使用する場合と比較して, 未知数の数を3分の1に減らし, 計算負荷 (直接ソルバーの場合) を最大で1桁減らすことができるため, 数値計算を行う上で魅力的です. また, スカラーポテンシャルを用いて定式化された問題の解析解を求めるのは一般的に非常に簡単であるため, 理論的な観点からも魅力的です.
ただし, 電磁気学における課題, そして誤解の原因の一つは, 大学で学ぶベクトル計算が, ほとんどの場合, スカラーポテンシャルで表現されるカールフリーの場の解析という特殊なケースから始まることです. 第一印象が大切という原則に基づき, 学生は卒業後に実社会の問題に直面したときに, ゼロ以外のカールのある場に必要なより複雑な解析について忘れてしまうことがよくあります. このブログは, そのギャップを埋めるのに役立つかもしれません.
ポテンシャルとゲージ変換の一意性について
ポテンシャルを使用するにあたって, ポテンシャルの一意性に関するいくつかの罠や落とし穴があります. すでに述べたように, 物理場\textbf{E}, \textbf{D}, \textbf{H}, および \textbf{B} はすべて, マックスウェル方程式によって決定されるように, 固有の解を持っています. ただし, スカラーポテンシャルとベクトルポテンシャルをマックスウェル方程式に代入すると, 追加の方程式や条件が適用されない限り, これらのポテンシャルは通常, 無限の解を持つことになります.
以下では, マックスウェル方程式の解を表現するために, スカラー電気ポテンシャル V, 磁気ベクトルポテンシャル \textbf{A} と, \textbf{E} と\textbf{D}, \textbf{H} と \textbf{B} の間の線形関係 (物質法則) を用いることを前提とします. 実際には, 提案されたポテンシャル (V, V_m, \textbf{A}, と \textbf{F}) を自由に組み合わせて, マックスウェル方程式が要求する \textbf{E} と \textbf{H} の非ゼロのカールと \textbf{D} の非ゼロの発散を表現することができます.
スカラーポテンシャル V から始めましょう. ファラデーの法則では誘導電場がないので, \nabla \times \textbf{E} = \textbf{0} となるように静的状態から始めます. 次に, \textbf{E} = – \nabla V と仮定できます. ただし, V は
C は定数のように一意に定義されるものではなく, 同じ静電場を生成します.
したがって, スカラーポテンシャルは, 一意の解を得るために, その大まかなレベルを固定する少なくとも1つの追加条件を必要とします. 多くの場合, これは境界条件 (接地電位または印加電位) として与えられます.
磁場のポテンシャル \textbf{A} に進むと, 物事はより複雑になります.
から, スカラー関数 \psi 勾配を, \textbf{A} に足せることがわかります.
これにより, \nabla \times (\nabla \psi)= \textbf{0} であるため, 同じ \textbf{B} が生成されます.
スカラー関数の勾配によってベクトルポテンシャルをシフトするこの方法は, ゲージ変換と呼ばれます. ヘルムホルツの定理に戻ると, このゲージの不確定さは, これまで \textbf{A} の回転のみを指定していたためだとわかります. (定数ベクトル \textbf{C} の追加を除けば) 一意のベクトルポテンシャルを得るには, \textbf{A} の発散も指定する必要があります. 後者は通常, 境界条件によって決定されます. \nabla \cdot \textbf{A} によく選ばれるのは, いわゆるクーロンゲージです.
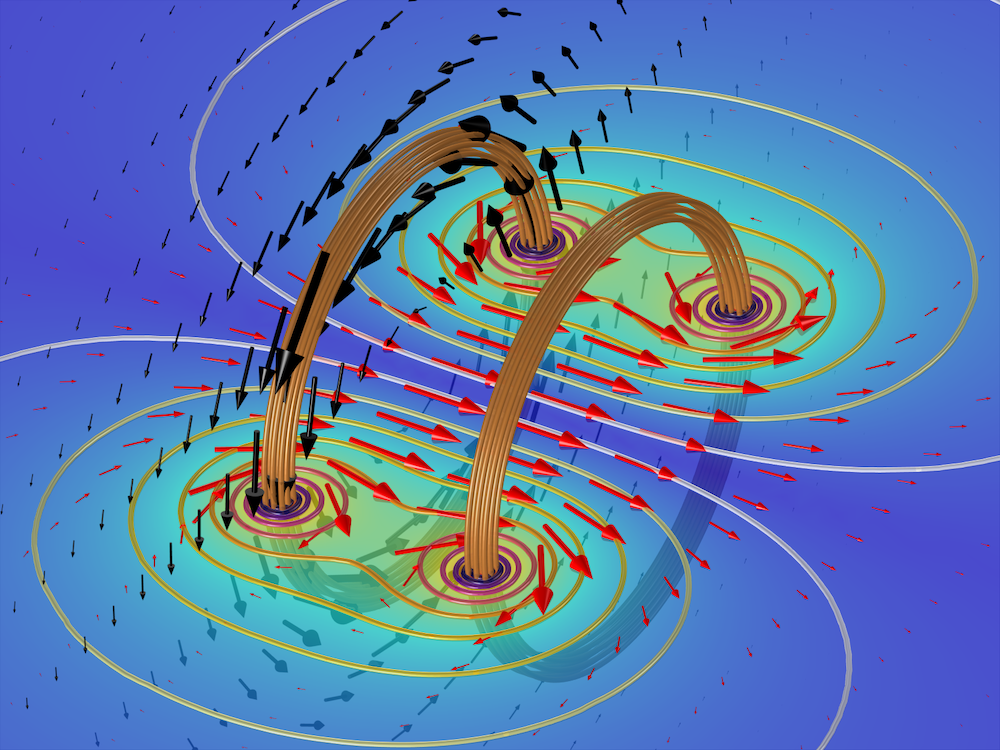
静的ヘルムホルツコイルの計算された \textbf{A} 場 (大きさを示す黒い矢印と等高線) と \textbf{B} 場 (大きさを示す赤い矢印とスライス). 各巻線は, \textbf{A} 場に平行に流れる等しい電流の10本の銅線ターンで構成されています. \textbf{A} 場は, クーロンゲージ \nabla \cdot \textbf{A} = 0 で計算されています.
電気力学におけるゲージ変換
これまでの説明では, 静止した状態で物質の動きがないと仮定していたため, 誘導電場も変位電流密度もありませんでした. これらの条件下では, 電場と磁場は一方向に結合されます. 静電場が DC 伝導電流密度を駆動し, それが次に磁場を生成します.
ここで, ゼロ時間微分の条件を緩和します. ファラデーの法則では,
であり, \textbf{B} = \nabla \times \textbf{A} を挿入した後は次のようになります.
次のように定義すると, ファラデーの法則が満たされます.
ただし, 前のセクションのゲージシフトの演習を繰り返すと, \textbf{E} の定義を変更しないために, \textbf{A} だけでなく V もシフトする必要があることがわかります. つまり,
したがって
これで, \textbf{A} と V の両方がゲージの選択に依存し, 両方とも \textbf{E} を \psi から独立させる方法で電場に寄与します.
また, ファラデーの法則で \nabla \times \textbf{E} の元になる項が – \frac{\partial\textbf{B}}{\partial t} であるのと同様に, マックスウェル・アンペアの法則では伝導電流密度と変位電流密度の項 – \sigma\textbf{E} + \frac{\partial\textbf{D}}{\partial t} を介して電場が磁場に影響を与えることにも注目してください. したがって, 動的な電場と磁場は双方向に結合されます (完全に結合された電磁気学または完全なマックスウェル定式化とも呼ばれます).
もう1つの非常に重要な点は, 電位は電場 \textbf{E} に部分的にしか寄与しておらず, ゲージに依存するということです. つまり, 電圧 U は次のように電場の線積分でしか定義できないということです.
したがって, カールのない電場の解析や回路解析に深く根ざした電位差を利用するという考え方は, 一般的には当てはまりません. さらに, 電気力学では, 測定される電圧は, 選択された積分パス L, 例えば, ピックアップコイルの向きに依存します.
ゲージを選択する方法はたくさんあります. クーロンゲージを使用すると, (遠く離れていても) 電荷密度の変化に即座に反応する電気ポテンシャルが得られるのに対し, 磁気ベクトルポテンシャルは, 有限の伝搬速度の影響を受けます. これは相対性理論と矛盾しているように思われるかもしれませんが, 電位は直接測定できないことに注意してください. 電場 \textbf{E} だけが, 電荷への影響を通じて測定可能であり, 定義上, ゲージの選択に影響されないのです.
ベクトルヘルムホルツ方程式
特に実用的なゲージは, 電位が次のように消失するように \psi を選択したゲージです.
このゲージは, 静的限界では劣化し, \textbf{E} が未定義のままになるため, 動的な定式化にのみ使用できます. これは, RF モジュールの電磁波 (周波数領域) インターフェースおよび AC/DC モジュールの磁場 (周波数領域) インターフェースで使用される, いわゆるベクトルヘルムホルツ方程式で使用されます. 前者の場合, 従属変数は \textbf{E} ですが, 後者の場合, それは \textbf{A} です. 数学的な観点からは, 周波数領域のように大きな違いはなく, 時間高調波規則 \textbf{E}(t,\textbf{r}) = Re(\textbf{E}(\textbf{r})e^{j\omega t}) を適用すると
となります. したがって, \textbf{E} と \textbf{A} は, グローバル係数 – j\omega だけが異なります.
磁場インターフェースを見ると, 周波数領域の方程式は次のようになります.
十分に低い周波数では, オメガを含む項は数値的に消滅し, 定式化は静磁気定式化と同じになります.
そうすると, 電気的な部分 (誘導電場 \textbf{E} = – j\omega\textbf{A} に関連する) が数値的に重要でなくなるため, V が消滅するゲージは事実上失われます. したがって, \nabla \cdot \textbf{A} の固定も数値的には重要でなくなり, \textbf{A} は一意に決まらなくなります.
これはすべて, 静的限界で電磁結合が失われた結果として見ることができます. 電場を表す別の方程式が必要になります(この場合 V は消滅しないため, 電場は V に基づいています).
つまり, ベクトルヘルムホルツ方程式は, 誘導された伝導または変位電流密度が数値的に重要である場合に限定されます.
A-V の定式化
低周波では, \textbf{A} と V の両方を解く定式化を行うことが好ましいです. これにより, ポテンシャルが静的限界で適切に分離できるようになります (\textbf{A} と V に対して別々であるが結合された方程式があります). その代わり, ゲージの不確定性を扱うための明示的な対策が必要になります. つまり, \nabla \cdot \textbf{A} に対する条件を指定しなければなりません. AC/DC モジュールの磁場および電場インターフェースは, \textbf{A} と V の両方を求解します.
結論
これまで, ヘルムホルツの定理をマックスウェル方程式に適用し, 物理場\textbf{E}, \textbf{D}, \textbf{H}, \textbf{B}を表すスカラーポテンシャルとベクトルポテンシャルを使用した場合の結果を見てきました. 結論は次のとおりです.
- ベクトル場を一意に決定するには, ベクトル場のカールと発散の両方を知る必要があります.
- \textbf{E}, \textbf{D}, \textbf{H}, および \textbf{B} は, マックスウェルの方程式と材料の法則によって一意に決定されます.
- マックスウェルの方程式にスカラーポテンシャルとベクトルポテンシャル \textbf{A} と V を導入することは実用的ですが, \nabla \cdot \textbf{A} が指定され, V の基準レベルがない限り, ポテンシャルは一意に決定されません.
- \nabla \cdot \textbf{A} の条件と V の一貫した定義の間には動的な関係 (ゲージ) が存在し, よって電場 \textbf{E} は選択されたゲージに依存しません.
- 電位 \textbf{A} と V は両方とも \textbf{E} に寄与するため, 電圧 U は, 経路に依存する線積分 U=\int_L{\textbf{E}\cdot}d\textbf{l} としてのみ測定できます.
- V=0 の特定のゲージでは, \textbf{A} または \textbf{E} に対するベクトルヘルムホルツ方程式が導かれ, 電磁波の伝播や誘導渦電流など, 十分に強い電磁結合を持つ効果のモデル化に有効です.
- しかし, 低周波では数値的に破綻するため,\textbf{A} と V の両方を用いた定式化が必要となります.
このブログシリーズの次の章では, 静磁気で特定のゲージを明示的に適用する方法と, 周波数領域 \textbf{A} と V の両方を解く場合についてご紹介します. また, 電荷保存, 連続の方程式がマックスウェル方程式に固有のものであること, そしてそれによって解の存在がソース電流がソレノイドの場合に限定されることについてもご説明します. 後者は, 静磁気学と低周波電磁気学の数値モデリングを成功させる上で重要な要素であることがわかります. 乞うご期待!


コメント (0)