
COMSOL Multiphysics® ソフトウェアでの静電容量の計算は簡単に見えます. 導体が2本しかない場合, 手順は簡単です. 1本の導体を接地に設定し, もう1本をターミナルに設定して, 解を計算します. 次に, 組み込み変数によって静電容量が算出されます. しかし, タッチスクリーン, 伝送線路, 静電容量センサーなど, 導体が2本以上ある場合はどうでしょうか. 標準的な教科書の用語がわからなくなった場合は, 静電容量行列を計算するこの実例に従ってください.
自己静電容量とは?
静電容量とは, 系が電荷を蓄える能力です. 接地された基準電位に対して物体の電位を1ボルト上げるために必要な電荷量で定義できます. 線形系では, これは
Q は電荷, V は接地に対する電位差, C は静電容量です.
多導体系に入る前に, 定義により, 単一の孤立した導体であっても, 無限遠にある接地された球殻を基準として定義される静電容量があることを思い出してください. 導電性球の場合, この自己静電容量は
この式を使用して, たとえば地球の自己静電容量を計算できます. これは約 710 マイクロファラッドです.
人間の体も, このように, 帯電することがあります.
したがって, 人間の体も自己容量 (体容量とも呼ばれます) を示します. 姿勢や周囲の領域に応じて, 体容量は 100 ピコファラッドの範囲にあり, 人間にチクチクする感覚を引き起こすことさえあります. たとえば, 朝に髪をブラッシングしているときに, 体容量が数千ボルトに簡単に充電される可能性があります. 一日を始める前に, しっかりと接地してください.
相互容量行列とマックスウェル容量行列の比較
一般的な電気系では, 複数の導体間の容量が最も重要です. 相互容量は, 寄生容量または浮遊容量とも呼ばれ, 電荷を保持する2つの物体の間に発生する望ましいまたは望ましくない容量 (電荷の蓄積) です. 帯電した物体を別の物体の近くに持ってくると, 静電誘導 (電磁誘導と混同しないでください) のプロセスにより, 最初の物体の電荷分布が変化します. 特に伝送系では, ライン間の容量結合は意図せず, ノイズを発生させる可能性があるため, 問題になることがよくあります.
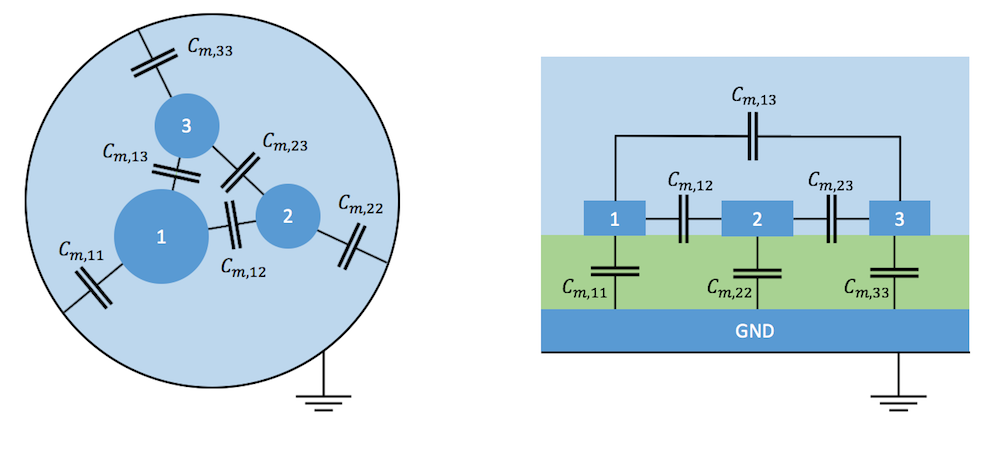
シールドされた3導体ケーブル (左) と, 接地プレート上のマイクロストリップ伝送線間 (右) の相互容量の一般的な例. 連続場モデルから離散コンデンサーを備えた集中モデルへの移行は, 導体を点に縮小し, その表面の電荷をそれらの間に示されているコンデンサーのプレートに移動することを意味します.
便宜上, N 本の導体と1つの追加の接地の系の相互容量を行列形式で配置することができます:
C_{m,11} & C_{m,12} & \dots & C_{m,1N} \\
C_{m,21} & C_{m,22} & \dots & C_{m,2N} \\
\vdots & \vdots & \ddots & \vdots \\
C_{m,N1} & C_{m,N2} & \dots & C_{m,NN}
\end{bmatrix}.
この行列の係数は部分容量または集中容量とも呼ばれ, 物理系を個別の要素のネットワークに縮小するときに回路シミュレーターで使用されます.
場の理論では, 別の行列形式がより一般的です. それは, マックスウェル容量行列です. 名前が非常に似ていて, 係数が同一ではないため, 相互容量行列とマックスウェル容量行列の関係を理解することが重要です. マックスウェル容量行列は, i 番目の導体の電荷と系内のすべての導体の電圧の関係を表します.
Q_1 \\
Q_2 \\
\vdots \\
Q_N
\end{pmatrix} =
\begin{bmatrix}
C_{11} & C_{12} & \dots & C_{1N} \\
C_{21} & C_{22} & \dots & C_{2N} \\
\vdots & \vdots & \ddots & \vdots \\
C_{N1} & C_{N2} & \dots & C_{NN}
\end{bmatrix}
\begin{pmatrix}
V_1 \\
V_2 \\
\vdots \\
V_N
\end{pmatrix}
マックスウェル容量行列係数 C_{11} は, 電位 V_1=1 のみで, 他のすべての電極が接地されているときに, 導体1の電荷を測定することによって決定できます. したがって, 行列は接地容量行列とも呼ばれます. その逆である C^{-1} は, エラスタンス行列と呼ばれます.
次のように, 自己容量と相互容量の寄与を合計して, 導体1の合計電荷を計算することもできます.
Q_1 &= &C_{m,11}V_1+C_{m,12}(V_1-V_2)+C_{m,13}(V_1-V_3)\\
&= & (C_{m,11}+C_{m,12}+C_{m,13})V_1-C_{m,12}V_2-C_{m,13}V_3)
\end{matrix}
N 本の導体にとって, 相互容量行列とマックスウェル容量行列の関係は次のように表されます:
Q_1 \\
Q_2 \\
\vdots \\
Q_N
\end{pmatrix} =
\begin{bmatrix}
\sum_{}{^N_{i=1}} C_{m,1i} & -C_{m,12} & \dots & -C_{m,1N} \\
-C_{m,21} & \sum_{}{^N_{i=1}} C_{m,2i} & \dots & -C_{m,2N} \\
\vdots & \vdots & \ddots & \vdots \\
-C_{m,N1} & -C_{m,N2} & \dots & \sum_{}{^N_{i=1}} C_{m,Ni}
\end{bmatrix}
\begin{pmatrix}
V_1 \\
V_2 \\
\vdots \\
V_N
\end{pmatrix}
マックスウェルの静電容量行列は, その負の非対角要素によって簡単に判別できます.
実例: 2つの球の相互静電容量
用語の定義が明確になったので, COMSOL Multiphysics で任意の導体系の静電容量行列を計算するのがいかに簡単かを見てみましょう. 足元にしっかりとした地面があると感じるために, 既知の解析解を持つ系から始めます. (解析解が大好きだと言いましたか? 実際, 新しいシミュレーションプロジェクトを開始するときは, 私はいつでも, 再現できる解析解を持つシンプルな系を見つけようとします.)
この場合, 半径 a と b の2つの導体球 (距離 c で分離) と無限遠の接地基準で構成される系を使用できます.
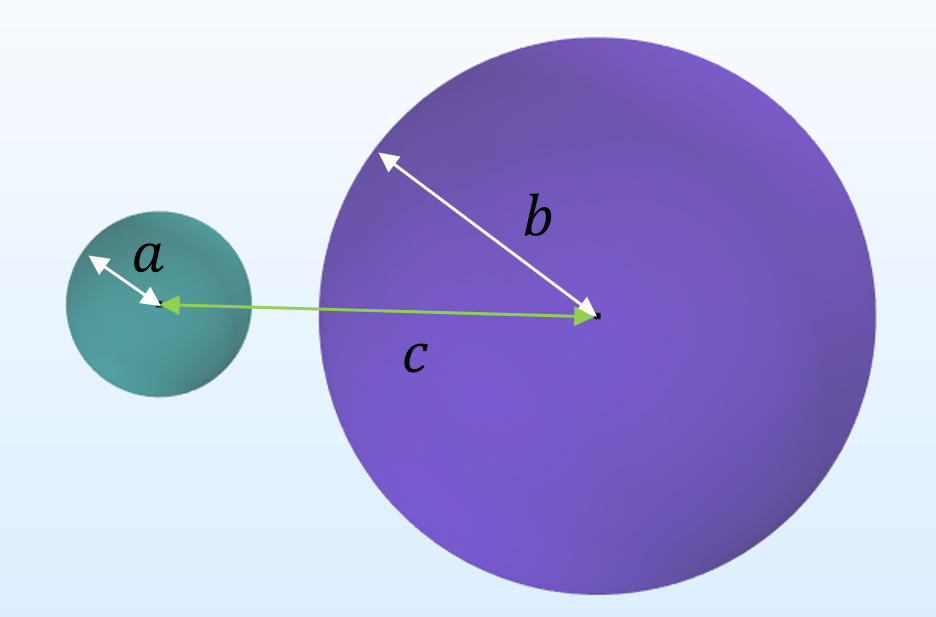
このような系の閉形式の表現は, マックスウェルの時代から知られています. 私は, de Queiroz (2003) と Lekner (2011) の2つの入手可能な出版物を参照しています. 3つのマックスウェル容量行列の表現は次のとおりです.
ここで
です.
COMSOL Multiphysics では, 合計演算子を使用してこれらの式を変数として簡単に宣言できます:

N のパラメトリックスイープでは, 球が互いに近すぎない場合に, シリーズが急速に収束することがわかります. 特定のパラメーター (a = 0.1, b = 0.3, c = 0.5) に対して, N を 10 に設定しても問題ありません.
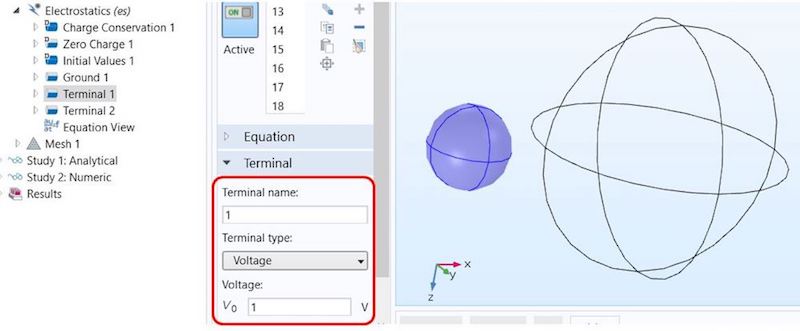
静電気インターフェースで静電容量行列を計算するために, 電位が 1 V の1つの球にターミナル条件を設定します.
次に, 機能を複製して2番目の球に適用し, 端子名を 2 に設定します. 静電容量行列を計算するには, 端子に異なる電圧または電荷パターンを適用する必要があります. 教育上の理由から, COMSOL® ソフトウェアのバージョン 5.3 でリリースされた, 大幅に高速化された新しい技術を紹介する前に, 従来の手動端子スイープについて説明します. 新しい技術は, 非常に一般的な問題の大規模なクラスで高速化されますが, 手動の方法の方が一般的です.
手動端子スイープは, 静電気インターフェースで直接有効化されます.

グローバルパラメーターセクションでスイープパラメーター名を宣言した後 (デフォルトでは PortName), PortName に対してパラメトリックスイープを実行できます.
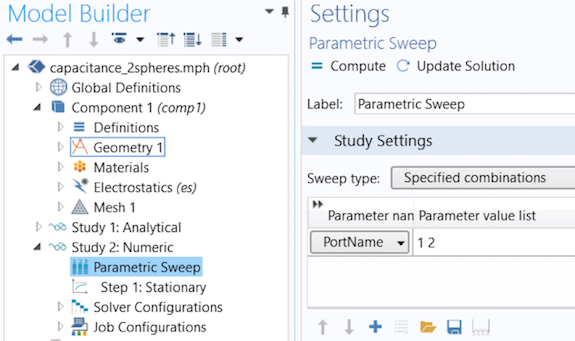
モデルでは, COMSOL Multiphysics ソフトウェアはスイープ中に1つの端子を 1 V に設定し, 他のすべての端子を接地します. その結果, 次の2つの解が生成されます:
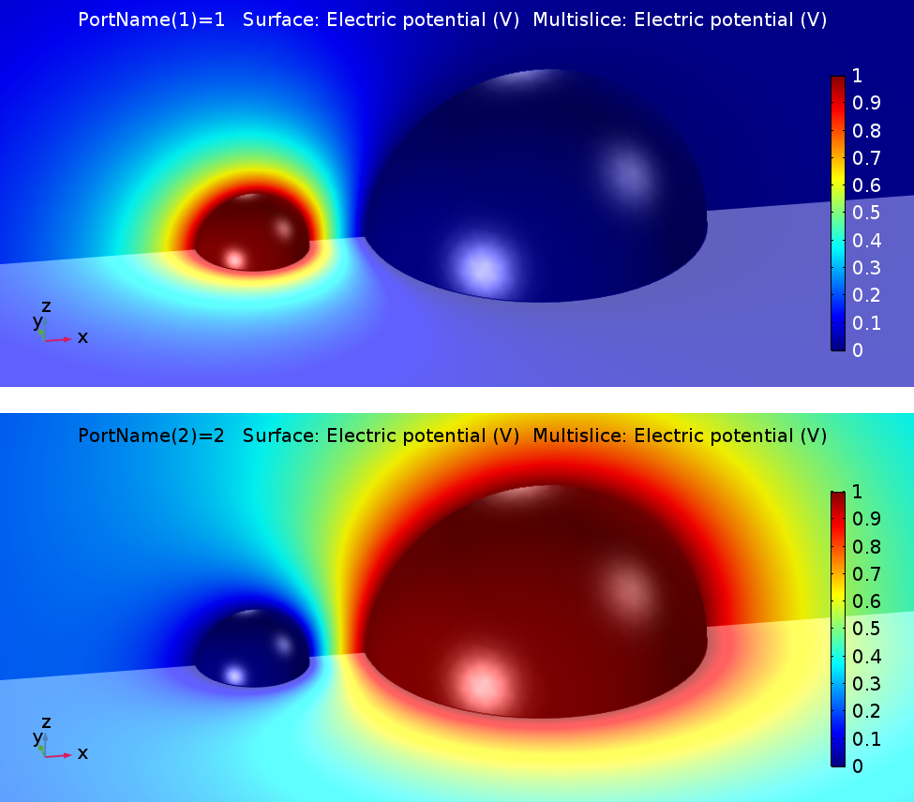
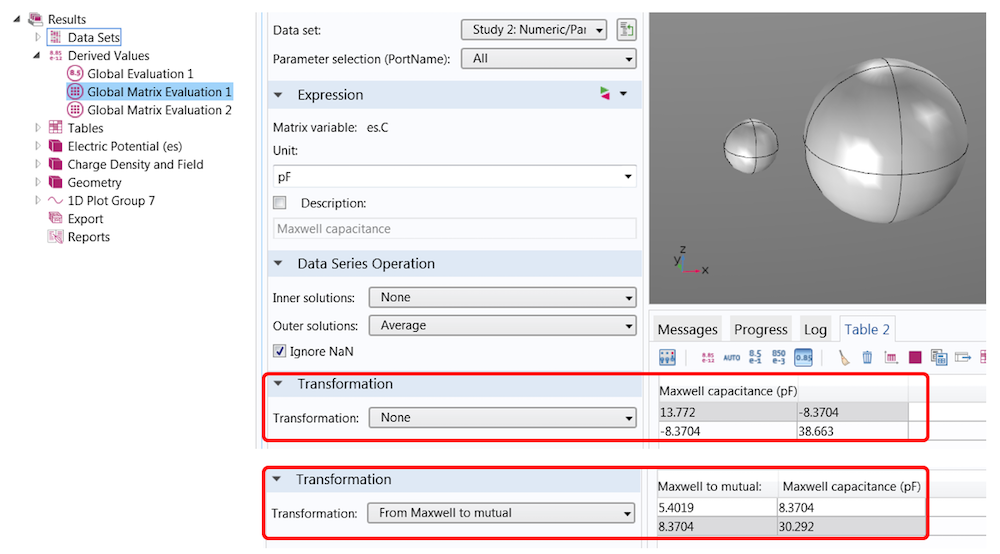
結果 > グローバル行列評価 を使用して, マックスウェル容量行列や相互容量行列など, さまざまな表記法で容量行列を抽出できます.
この単純な例では, それらの関係は
C_{m,11} & C_{m,12} \\
C_{m,21} & C_{m,22}
\end{bmatrix}
=
\begin{bmatrix}
c_{11}+c_{12} & -c_{12} \\
-c_{21} & c_{22}+c{21}
\end{bmatrix}
電圧端子ではなく電荷端子を設定する場合, 主な解決策は逆静電容量行列です. 電荷を上記の行列に変換するのに役立つ一連の変換が利用可能です.
定常ソーススイープと境界要素法による高速化
COMSOL Multiphysics バージョン 5.3 では, 多くの強力な新しいモデリング手法が導入されました. 静電容量行列の計算に特に関連する機能の1つは, 新しい定常ソーススイープスタディステップです.
PortName のパラメトリックスイープを使用する手動の端子スイープとは対照的に, この新しい技術では, 静電系に異なる電荷または電圧パターンを適用しても, 基礎となる FEM 方程式の系 行列は変更されず, その負荷のみが変更されるという事実を考慮しています. つまり, 行列を反転する必要があるのは1回だけで, 他のすべての負荷ケースで再利用できます. このアプローチは, 特に端子の数が多い場合や, 他のパラメトリックスイープ (ジオメトリ用など) が必要な場合に, 計算時間を大幅に短縮できます.
タッチスクリーンシミュレーターアプリのように, 端子の数が中程度の場合でも, 速度の向上は驚くべきものです. 同じ数の DOF を持つこのモデルでは, 私のマシンで 7.8 倍に達することができました!
新しい静電容量位置センサーチュートリアルモデルでは, 定常ソーススイープスタディステップを使用します.
定常ソーススイープは, セットアップも簡単です. 手動の端子スイープをアクティブにして, PortName 変数とパラメトリックスイープを定義する必要はありません. スタディステップを選択するだけで済みます. デフォルトでは, 調査はすべての端末で実行されます. 代わりに, カバーする特定のソースを定義することもできます.
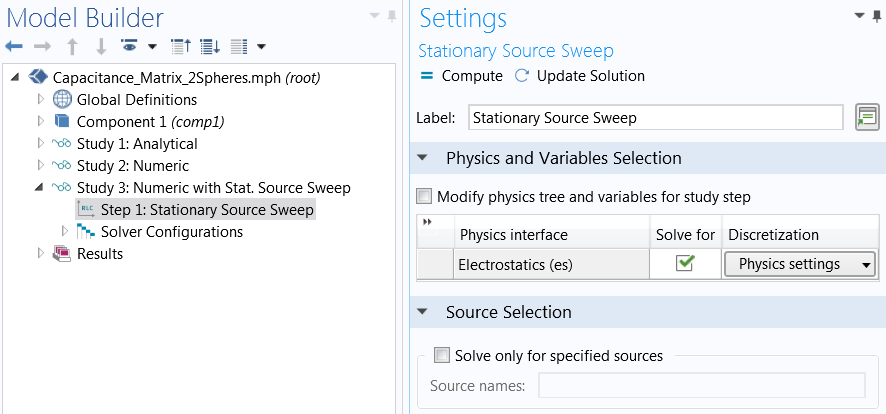
定常ソーススイープがそれほど強力であるなら, なぜ従来のアプローチを維持するのでしょうか?
システム行列の再計算が望ましい場合もあります. たとえば, 非線形またはマルチフィジックスの問題の場合や, 各ターミナル構成に合わせてメッシュを調整する必要がある場合などです. このような場合は, 手動のターミナルスイープの方が適しています.
COMSOL® ソフトウェアのバージョン 5.3 に付属するもう1つの強力な機能は, 静電気における境界要素法 (BEM) です. すべてのドメイン (周囲の空気ドメインを含む) のメッシュが必要な FEM と比較すると, BEM では無限空間でのメッシュ作成が回避されるため, DOF の数が少なくなります. 静電気における BEM と静電容量行列計算の組み合わせの詳細については, BEM を使用した静電容量位置センサーのモデリングチュートリアルを参照してください.
新しい BEM 実装についてもっと知りたいですか? この方法が腐食モデリングの簡素化にどのように役立っているかについては, 以前のブログをお読みください.
静電容量行列計算に関する結論
このブログでは, 静電容量行列の計算について検討し, さまざまな用語について説明し, 閉じた形式の解を持つよく知られた問題の数値解を提供しました. ここで紹介したシンプルなモデルは, 独自のモデルの参照として使用できますが, バージョン 5.3 でリリースされた新機能を使用すると, 多数の端子と追加のパラメトリックスイープを備えた大規模なモデルをより効率的に作成できます.
他の参考資料
- 静電容量と BEM に関する以下のブログを参照してください:
参考文献
- de Queiroz, A.C.M., 2003, “Capacitance Calculations“.
- Lekner, J., 2011, “Capacitance coefficients of two spheres”, Journal of Electrostatics 69(1):11-14.






コメント (0)