
輻射熱伝達をモデル化する場合, 輻射が表面からどのように放射され, 他の表面でどのように吸収されるか, また, 表面間でどの程度輻射が交換されるかを考える必要があります. このシリーズの以前の2つのブログで放射, 反射, 透過について取り上げましたが, 今回は形態係数の概念と表面間の輻射熱伝達の様々な計算方法を紹介し, 輻射熱伝達モデリングの基礎についての習得を締めくくります.
形態係数入門
下図のような, 薄くて平らな2つの物体を考えてみましょう. ここでは, 赤外線 (IR) 光がこれらの表面の周りの空間を自由に伝搬できると仮定します. これは真空中の場合に当てはまり, 室温付近の空気やその他多くの気体では妥当なことです. 逆に, 減衰しない伝搬を仮定することが合理的でない場合は, 次のとおりです.
- 水蒸気のなどの赤外線吸収性気体
- 高温の気体
- 微粒子が細かく分散している気体
- 化学反応中の気体
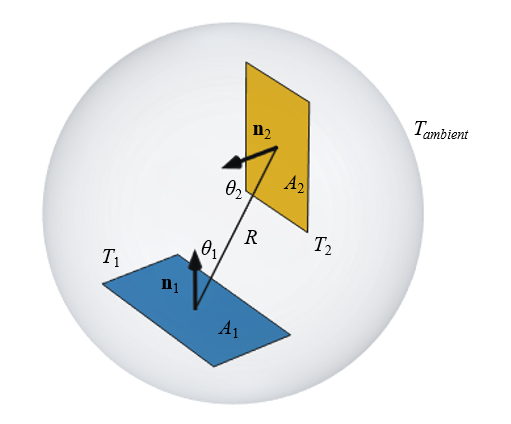
異なる温度にある2つの等温物体間で輻射熱伝達が発生します. この物体は, 周囲を包んでいる表面の中にあると考えることができます. 熱伝達の大きさは, 物体の大きさと向きに依存し, 互いに向き合っている表面間でのみ発生します.
ここでは, この2つの物体は異なる温度で固定されていると仮定します. この2つの物体の以外には, 考慮すべきモデルは何もありませんが, モデル化されていない周囲の空間についても, 1つの定義をする必要があります. 周囲温度または背景温度と呼ばれる, 均一な温度を定義しなければなりません. この周囲空間を明示的にモデル化することはしませんが, 周囲を包む固定温度の表面を想像すると便利です.
最初の物体を考え, それが発するすべての輻射を考えてみましょう. 輻射された熱流束の一部は周囲に向かい, 一部は2番目の物体に向かいます. ここで, 形態係数という概念を紹介します. これは, 表面1 (A_1) を出て表面2 (A_2) に到達する輻射の割合で, F_{12} と表記されます. 輻射率が均一で, 中間に妨害する面ないと仮定すると, これらの面間の形態係数は次のようになります.
系内に2つ以上の表面があるとき, それらがすべて互いに見える可能性があるので, 形態係数を F_{i j} と書き, i,j はモデルの N 個の相互作用するすべての表面のインデックスを表します. 任意の2つの表間には, 次のような相互関係が成り立ちます: A_i F_{i j} = A_j F_{ji}
なお, 表面が凹面であれば, F_{i i} >0 となります. また, 周囲への熱流束は, 周囲の形態係数 F_{i \rightarrow amb} = \left( 1 – \sum_{j=1}^N F_{ij}\right) によって定義されることにも注意してください. 閉じたキャビティの場合, 周囲の形態係数はゼロになります.
輻射熱交換を計算する3つの方法
輻射熱交換の計算方法は, 以下の3つです.
- 面積の直接積分
- ヘミキューブ
- レイシューティング
1. 直接面積積分法
直接面積積分法では, すべてのペアの表面に対して二重積分を実行します. 表面間に障害物や影がない限り, 使用することができます. この方法は, 輻射積分の次数によってのみ精度が制御され, 正確であることが証明されています.
この方法では, 常に相互関係が満たされますが, あまりに低い離散化と非常に粗いメッシュを使用した場合, 閉じたキャビティでは周囲の形態係数がゼロとは異なる場合があります. 直接面積積分法は, 要素が多い場合, 計算量が多くなります. また, シャドウイングを考慮しないため, 主に小さな凹型キャビティのモデリングに有効であり, 実際にはあまり使用されません.
2. ヘミキューブ
ヘミキューブ法は, 下の画像から概念的に理解することができます. 1つの表面要素を考え, その要素について5つの境界を描画し, それらを均一にピクセル化します. 次に, このピクセル化された境界に周囲の表面を投影し, 各表面に関連付けられるピクセルを数えることで, 周囲の表面からの輻射加熱がその要素にどれだけ照射されているかを判断します. これをすべての表面について繰り返します.
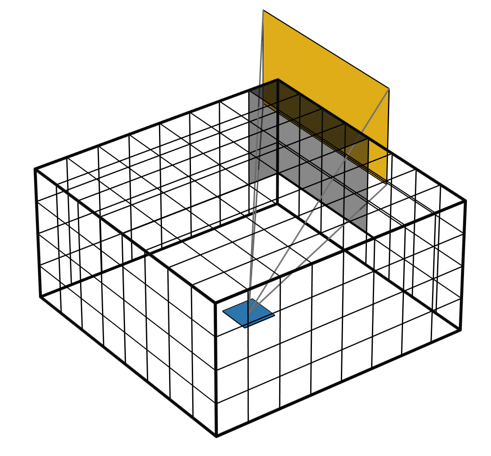
ヘミキューブ法は, 周囲の表面をピクセル化された特定の境界に投影して輻射照度を計算する方法です.
表面のシャドウイングは Z バッファーで効率的に処理されるため, 計算量が少なくて済みます. この方法の単一の設定項目, 輻射分解能は, ピクセル数を制御します. 輻射分解能を上げると相互関係の精度が向上し, 閉じたキャビティの周囲の形態係数は常にゼロになります.
3. レイシューティング
レイシューティング法は, 角度依存の輻射率, 鏡面反射率, または半透過率などがある場合に有効です. レイシューティング法は, その名の通り, 空間に光線を射出する方法です. しかし, これは逆光線追跡法であることに注意する必要があります. 各要素の評価点から, 外に向かって光線を照射し, その方向からの輻射照度を求めます. つまり, 光線は入射光と反対方向に向かうと考えることができます. これらの光線は, 周囲の半球状空間からの全輻射照度の有限サンプリングを表しています.
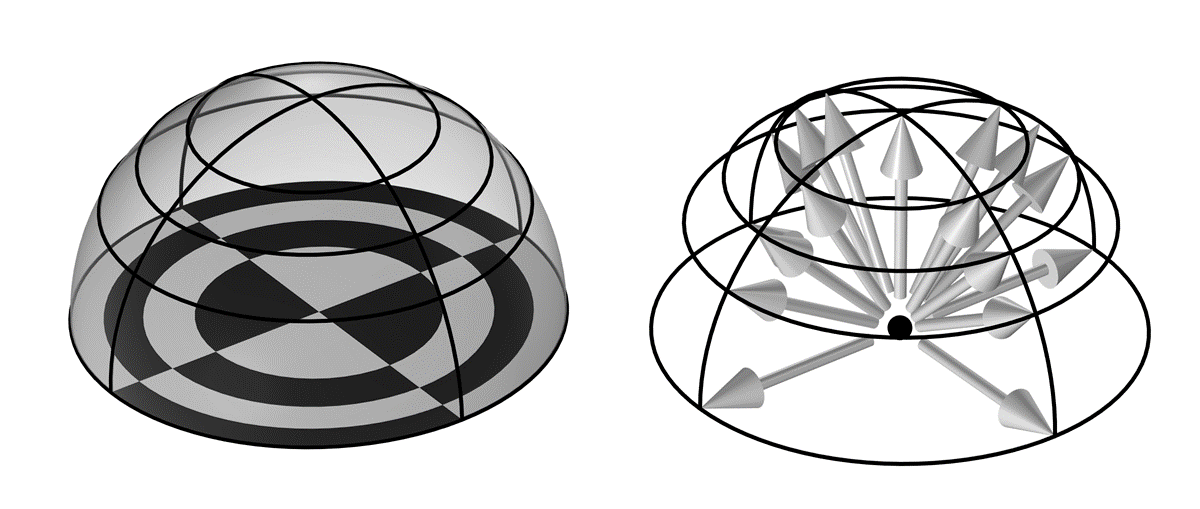
輻射分解能が4の場合の, 3D 半球の離散化に関するレイシューティング法の図. ベースとなるチェッカーボード (左) の16枚のタイルの面積はそれぞれ同じです. 矢印は, 半球上の各タイルの角を指しています (右).
レイシューティング法には, 要素の順番と同様に, 6つの変更可能な設定項目があります. この中で最も理解すべきは輻射分解能で, 上の画像で輻射分解能を n_{res}=4 とした場合のように, 半球 (3D) または半円 (2D) 上の光線の初期分布を定義するものです.
この方法は, まず周囲を3D で n_{res}^2 個のタイル (2D では n_{res}) に細分化し, 各タイルの角に光線を描画することから始まります. これらのタイルはそれぞれ同じ形態係数を持ち, ヌッセルトの類推により, 下の平面への各タイルの投影面積が等しいことを意味します. 2D の半円の場合, 下図のように周囲は n_{res} 個のタイルに分割され, それぞれの平面への投影面積が等しくなります. このため, 下図のように, 光線の角度分布が不均一になることに注意してください.
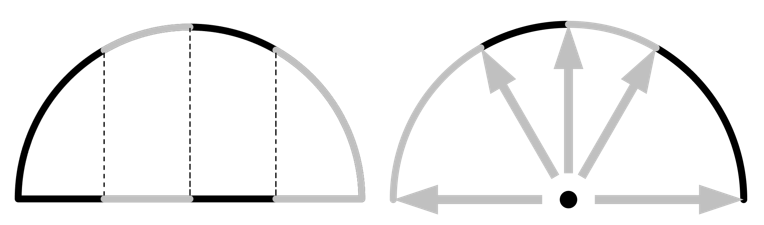
2D の場合のレイシューティング法の図. 半円の各セクター (左) は, 下の線上に等しい投影面積を持っています. 矢印は各タイルの角を指しています (右).
光線が外側に照射されるとき, 基本的にその方向から来る熱流束を参照し, 隣接する光線から来る熱流束と比較します. 許容値設定で定義された熱流束に差がある場合, レイシューティング法は, 最大アダプト数オプションで指定された値まで, 間に追加の光線を導入し始めます. 光線が鏡面反射面, または透過面に当たると, 最大反射数まで, その表面からも追加の光線が発射されます. 鏡面反射率が0.99を超えるキャビティ内部で多くの反射を扱わない限り, デフォルトの1000が妥当です.
角度依存の特性設定は, 角度依存の輻射率を持つ表面がある場合にのみ適用できます. デフォルトのフル分解能設定は, 角度依存関数をどれだけ細かくサンプリングするかを指定できる補間関数オプションと比較して, 最も正確なだけでなく, 最も計算量が多い設定となっています.
結果の信頼性を確保するために検討する必要があるのは, 主に輻射分解能と最大アダプト数であり, これらの設定の相互関係を理解することが重要です. 2D のケースを見て, 中心にある要素から射出される光線を考えてみましょう. このプロットはあくまでも視覚的なものであり, 計算光線そのものをプロットすることはできないことに注意してください. ここでは, 周囲に単位輻射率 (反射率ゼロに相当) の半円があると考えます. 温度は均一かつ一定で, つまり, 各光線が同じ輻射負荷を受けます. この場合, 最小限の輻射分解能でも束の正しい答えが得られます. 分解能を上げても (光線の数を増やしても) 精度が上がることはなく, アダプトが発動することもありません.
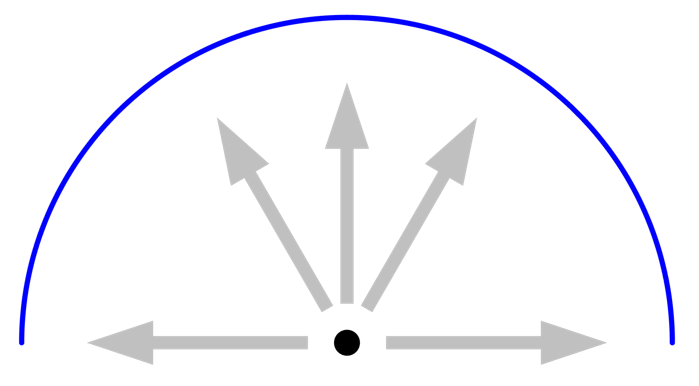
次に, 同じように単位輻射率の, 温度が異なる小さな物体を, たまたま光線方向の1つと正確に一致する角度の位置に導入してみましょう. この光線は, 隣接する光線とは異なるものを見ることになり, 下図のように角度空間が細分化されます. 最大アダプト数を増やすと精度が上がりますが, 小さな物体はすでに最初の光線の1つによって見えているので, 光線の分解能を上げる必要はありません. この光線のアダプトは, 異なる光線からの異なる輻射照度を検知することによって発動するため, 単一の表面が輻射束の空間的変化を持つ場合にも使用できます.
一つの光線から見える小さな物体を導入すると, 隣接する空間の光線もアダプトされます. アダプト数が高ければ高いほど, 精度が上がります.
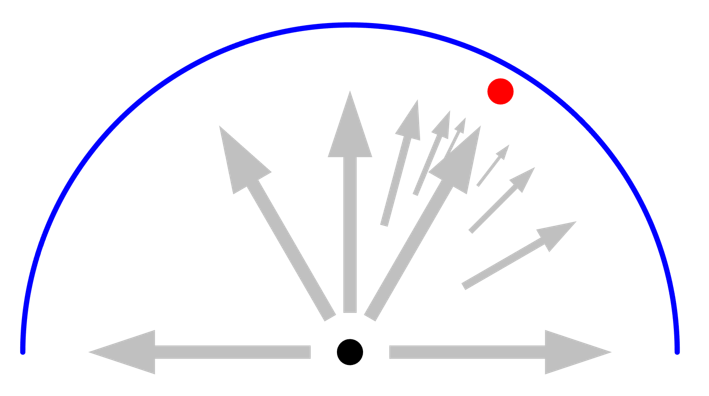
最後に, 初期の輻射分解能方向の1つと一致しない別の角度位置に, 別の小さな物体を導入してみましょう. この場合, 最大アダプト数は関係ありません. この2つ目の物体は, どの初期光線によっても見られることはありません. この2つ目の物体を見るためには, 輻射線の分解能も上げなければなりません.
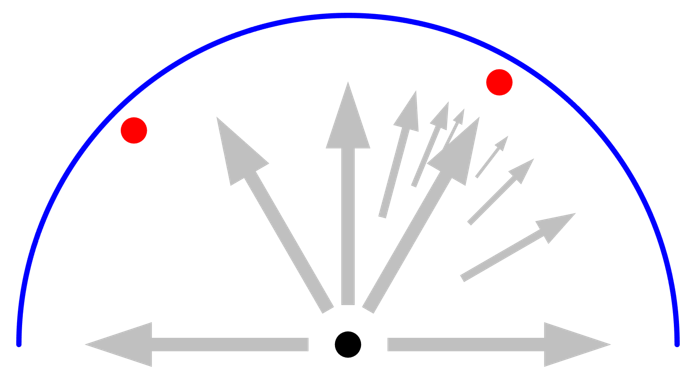
分解能で定義されているように, 初期光線の1つから小さな物体が見えない場合, 近くの光線ではアダプトが実行されず, 見落としてしまうことになります. この場合, 輻射分解能を上げる必要があります.
輻射グループを使う
上記のすべての方法と並行して, いわゆる輻射グループを使用することもできます. 特に複数の異なるキャビティを持つモデルでは, 互いにしか見えない境界のセットを選択することで, 計算コストを削減することができます. ただし, グループ分けを誤ると誤った結果が出ることがあるので, グループは慎重に使用する必要があります.

異なる表面のセットが他の表面を見ることができない場合, グループ機能を使用するのが合理的です. 左図では, 異なる色で合理的なグループ化を示しています. 右のケースは, グループの使用にはあまり適していません.
その他の表面から表面への設定
移動または変形する物体を含むモデルでは, 形態係数がしきい値を更新の設定により制御されるように, 形態係数を更新する必要があります. 非線形反復ごとに更新するデフォルト設定は, 最も正確な結果を出しますが, コストが高くかかる場合があります. 形態係数の更新を完全にオフにすることも可能です. これは, 形態係数にほとんど影響を与えずに移動または変形している物体の場合に合理的です. また, 時間的にまたはユーザー定義の式で定期的に更新することも可能です.
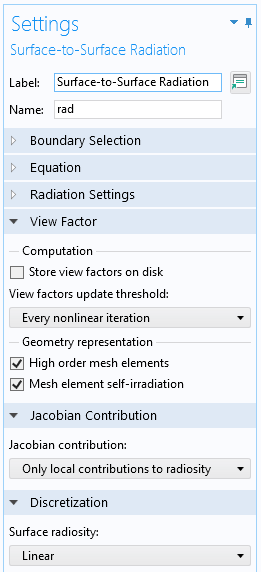
表面‐表面輻射インターフェースの形態係数の設定.
形態係数の設定では, 形態係数をディスクに保存することも可能です. これは大きなモデルの場合, 時間を節約することができますが, 特にヘミキューブ法の場合, ディスク上のモデルファイルのサイズが大幅に大きくなります. この設定は, ジオメトリが変わらない場合にのみ使用することをおすすめします.
ジオメトリ表現設定は, ジオメトリの形状関数が線形より高い場合に使用されます. 離散化を高くすると, これらのオプションは要素の曲率を考慮するようになります.
最後に, ヤコビアンへの寄与は, デフォルトでラジオシティへの局所的な寄与に設定されます. このデフォルト設定は, COMSOL Multiphysics® ソフトウェアのバージョン 6.0 以降, メモリ使用量の低減と解析時間の短縮につながります. ただし, モデルが純粋に輻射冷却されており, 表面間で大きな温度差がある場合には, 失敗することがあります. 非収束が見られる場合は, この設定を全照射の寄与を含むに変更します.
形態係数の評価とプロット
表面のセットが複数あり, それらの間の形態係数を知りたい場合は, 以前のブログで取り上げたものを参照にしてください. また, モデル内の1つの表面から他のすべての要素への形態係数をプロットすると役立つ場合があります. これは, 各要素に対してガウス積分を実行する elemint (order,expression) 演算子を使って行います. 積分の次数は最初の引数で与えられ, 形態係数を評価するために, 式の中の radopu() and radopd() オペレーターを使用します. 例えば,
elemint(1,comp1.rad.radopu(S1,0))/intS1(1)/dvol
という式をプロットすると, 要素ごとに, 積分演算子 intS1() で定義された表面のセットからモデル内の他のすべての表面への形態係数を評価することになります.
変数 S1は, 照射されている表面のセットでは1と定義し, すべての照射されている表面では0とします. このようなプロットの例を以下に示します. 照射されている要素の大きさである変数 dvol をさらに割ることにより, 以下のように1つのセットの表面からの光度に対応するプロットが得られます.
球体から互いに影を落とす2つのブロックへの照射に対応する可視化.
最後に
ここまでで, 非関与媒質に囲まれた表面間の輻射熱伝達をモデル化するための3つの重要な概念的要素について見てきました. まず, 高温の表面が熱輻射を放射するさまざまな方法について紹介しました. 次に, 表面に入射した輻射がどのように吸収, 反射, 透過されるかについて話しました. 最後に, 形態係数とその計算方法, 更新方法について説明しました. これで, 自信を持って熱輻射を扱える準備が整いました!






コメント (0)