
私たちは3次元の世界に住んでいます. 時空を考えると, おそらく4次元の世界と言えるでしょう. しかし, エンジニアリング解析では, モデリングと計算リソースの両方を節約するために2D近似を使用するのが一般的です. このブログでは, 固体力学の分野で2D定式化を用いて問題を検討することができる場合とその方法について見ていきます.
2Dとは?
現実では実際に二次元と呼べるものはあまりありません. たとえば, ケーブルの断面の周りの電磁界を2Dで調べるとき, 実際には次のように状況を捉えています. このケーブルはまっすぐで長く, 端から十分に離れているため, 場はこの断面平面内の位置にのみ依存する. ほとんどの物理的な問題の場合, このような考え方をします. 2D近似では, 最終的な影響を無視して, 長く真っ直ぐなオブジェクトの断面を調べます.
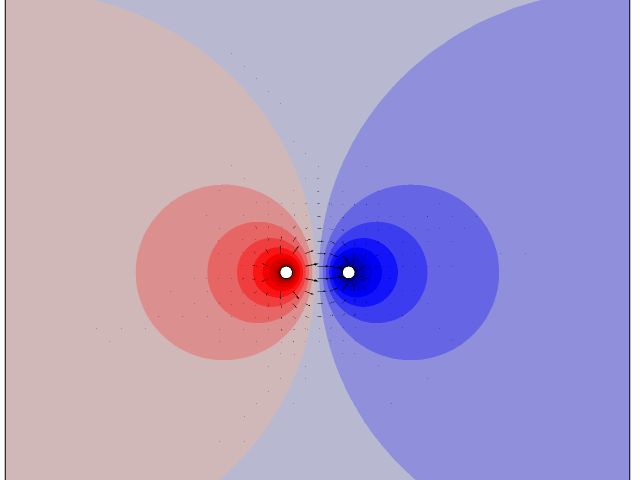
2Dで計算された, 電位の異なる2本の長いケーブルの周りの電位(色分け)と電場(矢印).
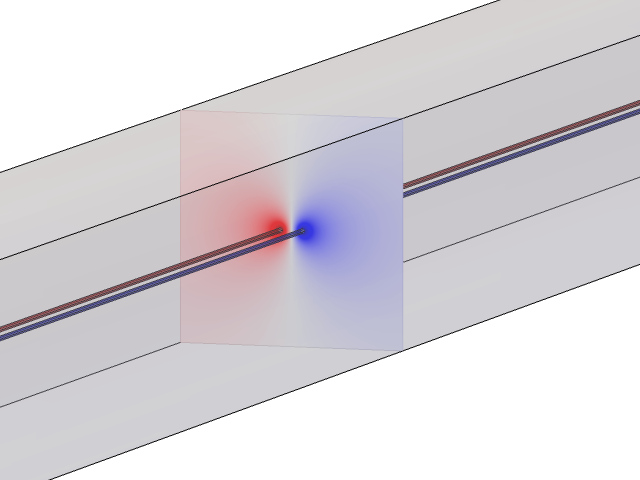
断面は, ケーブルが長く, まっすぐで, 平行である状況を表しています.
なぜ固体力学は特別なのか?
固体力学の分野では, 非常に長い押し出しよりも2D状態の方が多く見られます. たとえば, 平面にのみ荷重がかかった薄い平板を2次元と見なすことができます. では, このようなことを可能にする固体力学の特殊性とは何でしょうか?
同じプレートの熱伝達の解析を検討してみましょう. その場合, 大きな表面からの対流と輻射が面外方向に発生します. そうなると, 厚さ方向の温度勾配が重要となってきます. したがって, 薄板の熱伝達の2D近似はより困難となります. 同様の推論は他の多くの物理現象にも適用できます.
固体力学の場合, 面外方向にも影響があります. 薄板は, 一般的に横方向に変形します. たとえば, 伸ばすと薄くなります. ただし, それは2D問題の求解には直接影響しません. ちなみに, 興味のある方のために, 厚みの変化は, 事後的に計算できる結果です. これについては, 以下で詳しくご説明します.
固体力学のためのさまざまな2D定式化
次のセクションでは, 2Dがxy平面を意味し, zが面外方向であると想定しています. xy平面の変位はそれぞれuおよびvと呼ばれ, wはz方向の変位です.
面内作用と面外作用の間にカップリングがない場合(たとえば, 線形弾性材料のポアソン比がゼロの場合), すべての定式化が同一になることにご注意ください.
平面ひずみ
平面ひずみは, 近似を含まない2D固体力学の定式化の1つです. 平面ひずみの状態は, 2つの剛体壁の間でz方向に拘束されているオブジェクトに見られます. これは, 他の物理学分野の2D定式化に概念的に最もよく対応する定式化でもあります. ただし, オブジェクトはz方向に長い必要はありません. これが, 他のほとんどの物理学分野の2D近似との根本的な違いです.
仮定は単純です. z方向の変位は無し.
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) \\
v&=&v \left ( x,y \right ) \\
w&=&0
\end{array}}
{\ }
\]
これは等価的にひずみで表すことができます.
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) \\
v&=&v \left ( x,y \right ) \\
\varepsilon_{zz}&=&\varepsilon_{xz}&=&\varepsilon_{yz} &=& 0
\end{array}}
{\ }\]
なお, 端部効果を完全に回避するためには, 実際には剛体壁での境界条件がローラー型であることを前提としており, xy平面での変位は抑制されないことにご注意ください. もしそうでなければ, 端から離れた長いオブジェクトを研究するという振り出しに戻ってしまいます.
平面応力
平面応力の定式化では, z方向に関連する3つの応力テンソル成分がゼロであると仮定しています. これは, 薄い板の場合には良い近似ですが, 厚さがゼロに近づく極限でのみ完全に成立します.
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) \\
v&=&v \left ( x,y \right ) \\
\sigma_{z}&=& \sigma_{xz}&=&\sigma_{yz}&=& 0
\end{array}}
{\ }\]
自由表面では, これがまさに境界条件であるため, 常に局所的な平面応力の状態が支配的です. これが, 平面応力の仮定が非常に有効である理由です. この仮定は, プレートの反対側の2つの側面に正確に当てはまり, 厚さが薄い限り, 内部に大きなz方向の応力が発生することはありません.
一般化された平面ひずみ
残念ながら, 一般化された平面ひずみの一意的定義はありませんが, 一般的には, 通常の平面ひずみの定式化のいくつかの仮定が緩和されていることを意味します. ひずみテンソル全体がゼロでないことが許されているが, それでもxとyにのみ依存しないと仮定します. そうすると, 次のような変位場が, このようなひずみテンソルを出すことができます.
{\begin{array}{*{10}{l}}
u&=&u \left ( x,y \right ) – \frac{a}{2} z^2 \\
v&=&v \left ( x,y \right ) – \frac{b}{2} z^2 \\
w&=&\left (ax + by +c \right )z
\end{array}}
{\ }
\]
ここで, a, b, cは定数です. 微小な面外ひずみは次のようになります.
{\begin{array}{*{10}{l}}
\varepsilon_{zz}&=&ax +by +c \\
\varepsilon_{xz}&=&\varepsilon_{yz}&=&0
\end{array}}
{\ }
\]
解析が実行されるz = 0平面では, wはゼロです. したがって, 求解すべき変位場の成分はuとvの2つのみです. ただし, a, b, cの3つの新しい未知数があります. 一般化された平面ひずみの一般的な解釈では, 係数cのみが使用されます. 物理的には, これは長いオブジェクトがz方向に軸方向に拡張できることを意味します. パラメーターaとbも含まれている場合, 押出しは一定の曲率で曲がることもできます. a, b, cの値は, 断面に正味の軸力や曲げモーメントが作用していない, つまり端が自由であるという前提で決定されます.
COMSOL Multiphysics で一般化された平面ひずみオプションを選択すると, 純粋な軸方向の伸びを仮定するか, 曲げを含めるかを選択できます.
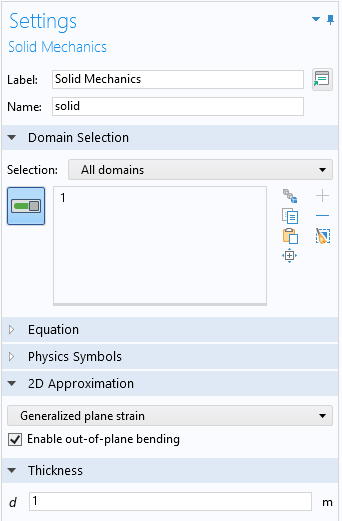
一般化された平面ひずみの選択.
一般化された平面ひずみと呼ばれることもある他の定式化もあります. たとえば, 面外せん断ひずみ\varepsilon_{xz}と \varepsilon_{yz}はゼロ以外の数値でも許容されます. このような定式化は, \varepsilon_{zz} = 0とともに, 弾性波 (陽的時間発展)インターフェースの2Dバージョンで使用されています.
構成モデル
線形弾性の仮定の下で, フックの法則は平面ひずみと平面応力に特化できます. フックの法則の完全な3D形式は次のとおりです.
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\sigma_z &=&\frac{E}{1+\nu} \left ( \varepsilon_{zz} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + \varepsilon_{zz} \right )\right ) \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 2G \varepsilon_{yz} \\
\tau_{xz} &=& 2G \varepsilon_{xz} \\
\end{array}}
{\ }
\]
ここで, Eはヤング率, vはポアソン比, Gはせん断弾性率です.
平面ひずみ
平面ひずみのケースは簡単です. 次の3D定式化からゼロである3つのひずみ成分を削除するだけです.
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} \right )\right ) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} \right )\right) \\
\sigma_z &=&\frac{E \nu}{(1+\nu)(1-2 \nu)} \left( \varepsilon_{xx} + \varepsilon_{yy}\right ) &=& \nu \left ( \sigma_x + \sigma_y \right )\\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
平面応力
平面応力のケースでは, \sigma_z = 0であることによって\varepsilon_{zz}を削除でき, 次のようになります.
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1-\nu^2} \left( \varepsilon_{xx} +\nu \varepsilon_{yy} \right) \\
\sigma_y &=& \frac{E}{1-\nu^2} \left( \varepsilon_{yy}+\nu \varepsilon_{xx} \right) \\
\sigma_z &=& 0 \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
次に, 横ひずみ(したがって厚さの変化)を解から\varepsilon_{zz} = – \nu (\varepsilon_{xx} + \varepsilon_{yy})として計算できます.
ただし, COMSOL Multiphysics® ソフトウェアでは, この定式化は使用されません. 代わりに, 完全な3Dフックの法則が, \varepsilon_{zz}の追加の未知の場とともに使用されます. もちろん, これにより問題全体の規模が大きくなりますが, メリットは非常に大きくなります. すべての材料モデルについて特別な平面応力形式を考慮する必要はなく, 熱膨張や同様の機能などを変更する必要もありません. ただし, 横応力\sigma_{z}をプロットしてみると, フックの法則を用いてひずみ場から計算されているため, 同一のゼロではないことに気づきます.
一般化された平面ひずみ
このケースはやや複雑です. 面外ひずみの仮定が構成関係に注入されると, 応力成分は, 係数a, b, およびcを介して座標xおよびyに陽に依存するようになります.
{\begin{array}{*{10}{l}}
\sigma_x &=& \frac{E}{1+\nu} \left( \varepsilon_{xx} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\sigma_y &=&\frac{E}{1+\nu} \left( \varepsilon_{yy} +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\sigma_z &=&\frac{E}{1+\nu} \left( ax +by +c +\frac{\nu}{1-2 \nu} \left ( \varepsilon_{xx} + \varepsilon_{yy} + ax +by +c \right )\right) \\
\tau_{xy} &=& 2G \varepsilon_{xy} \\
\tau_{yz} &=& 0 \\
\tau_{xz} &=& 0 \\
\end{array}}
{\ }
\]
非圧縮性材料
圧縮性の程度が低いほど, 面内作用と面外作用の間のカップリングが強くなります. 特に, 塑性, クリープ, および超弾性の多くのモデルは, 非圧縮性を前提としています. このような材料モデルを使用する場合, 選択した2D仮定の効果は特に強くなります.
どの定式化を選ぶべき?
中央に円形の穴がある長方形のプレートの単純なケースを見てみましょう. 非常に薄い板から始めて, 穴が長いトンネルのようになっている厚いオブジェクトへと進んでいきます.
面内プレートの寸法は2 m x 1 mで, 穴の直径は0.4mです. 1MPaの引張荷重が加えられます. 鋼の材料データが使用されます. 平面応力解を以下に示します.
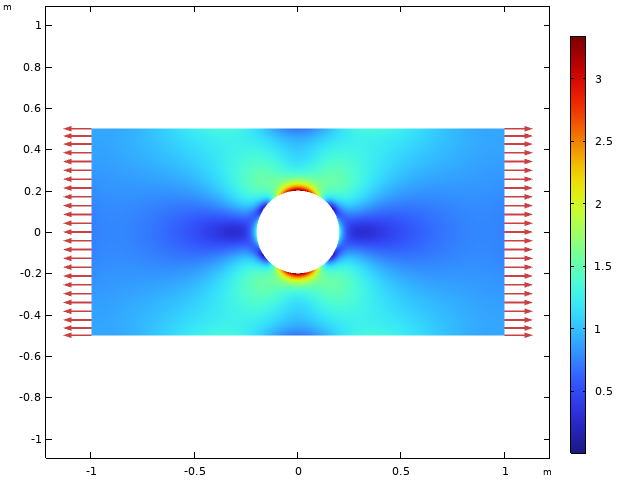
平面応力の仮定を使用した, フォン・ミーゼス等価応力.
平面応力の仮定の下では, 横応力\sigma_{z}はゼロです.
次に, 完全な3D解に目を向け, 同じオブジェクトをもう一度見ていきますが, 厚さはそれぞれ0.1, 1, 10mです. 下の図では, 横応力\sigma_{z}がプロットされています.
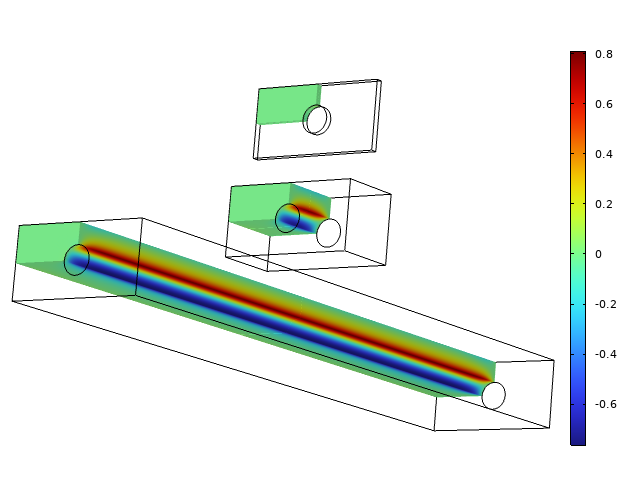
3つの異なる厚さの横応力.
薄い構成では横応力は無視できるため, 平面応力は適切な仮定であると言えます. 中間の厚さでは, 応力状態は完全に3次元です. 長いオブジェクトでは, 端部を除いて, 一定の横応力が支配的です. 最大横応力は0.8MPaであるため, 加えられた荷重と比較して, 決して無視できないことにご注意ください.
以下では, 穴の上部で最も応力がかかった場所での横応力をより詳細に調べます.
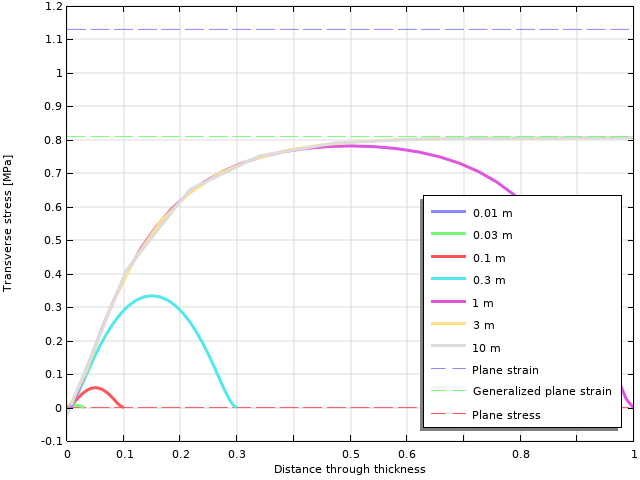
厚さによる横応力の変化. グラフのパラメーターは, オブジェクトの厚さです.
ご覧のように, 厚さが1m以上である限り, 約0.8MPaのピークレベルに達します. 厚さが薄いほど, 最大横応力は急速に低下します.
このグラフを見ることで, よくある2つの誤解を解くことができます.
- オブジェクトが横方向に自由であるからといって, それが平面応力の状態であるとは限らない.
- 長いオブジェクトは, 必ずしも平面ひずみの状態にあるとは限らない. これは, 両端が固定されている場合に限る.
実際には,
- 自由境界のある薄いオブジェクトは, 平面応力で近似可能.
- 自由境界のある長いオブジェクトは, 端から離れて, 一般化された平面ひずみで近似可能.
- 面内寸法に匹敵する厚さのオブジェクトは, 完全に3Dと見なす必要がある.
実は, 厚みのあるオブジェクトは平面ひずみの状態にあると考えるべきだという記述は, 教科書やネット上のあらゆる場所で見受けられます. このような状況では, 平面ひずみの方が平面応力よりも近似性が高いのは事実ですが, それでも正しいとは言えません. 一般化された平面ひずみの仮定の方が優れています.
私の個人的な推測では, 2D解での作業は, たとえばエアリー応力関数を使用して, ペンと紙で多くの問題が求解されていた時代にさかのぼるため, 選択肢は平面応力と平面ひずみのどちらかだったのではないでしょうか. 有限要素ソフトウェアでは, 厚みのあるオブジェクトの場合, 完全な3Dまたは一般化された平面ひずみがより良い選択肢となるのです.
なぜ横応力が発生する?
上記の例では, オブジェクトが横方向に自由に移動できる場合でも, 横方向に大きな応力が発生することがわかりました. なぜでしょう? ポアソン比効果により, 面外方向の厚さが変化するからです. 面内状態で応力(およびひずみ)勾配がある限り, この厚さの変化は均一ではありません. プレートの穴のように応力が集中すると, 最も応力がかかった点の材料は, 周囲の材料よりも薄くなろうとします. 隣接する材料はそれに反発し, 変形を抑制しようとします.
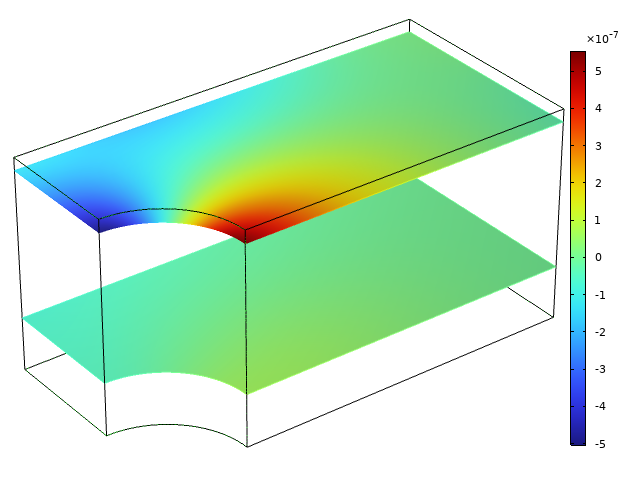
自由表面から遠く(下)および自由表面近く(上)の横方向変位の変動. 各平面で, 平均変位はゼロに設定されています.
前節では, 横方向の応力の大きさが自由境界からの距離によって異なることを述べました. 下図に示すように, 応力分布の詳細も自由表面からの距離によって異なります.
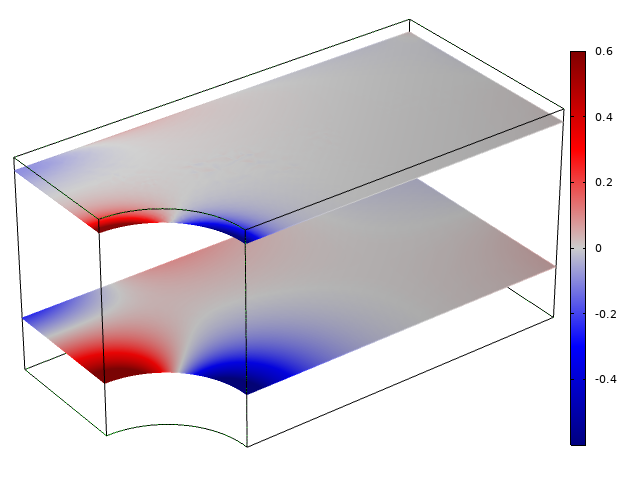
自由表面から遠く(下)および自由表面近く(上)の横応力の分布. 応力場は, 両方の切断面で同じピーク値を持つようにスケーリングされます. 実際の応力は, 境界に近いほど低くなります.
自由表面から遠く離れた横応力は, 面内ひずみ\varepsilon_x+\varepsilon_yに正比例します. 断面全体は, 周囲の材料からの拘束効果により, ほぼ均一な暑さを維持します. ただし, 自由表面の近くでは, 面内ひずみの勾配が大きいところ(この場合は穴の縁に近いところ)では, 横方向の応力が高くなります.
面内応力はどうか?
構造物が牽引力によってのみ荷重を受ける(規定の変位ではない)限り, 面内応力状態は, 少なくとも線形弾性については, 2Dの仮定とは無関係です. しかし, これがすべてではありません. 次の図では, x方向の応力は, 穴の上部で最も応力がかかっている位置に示されています.
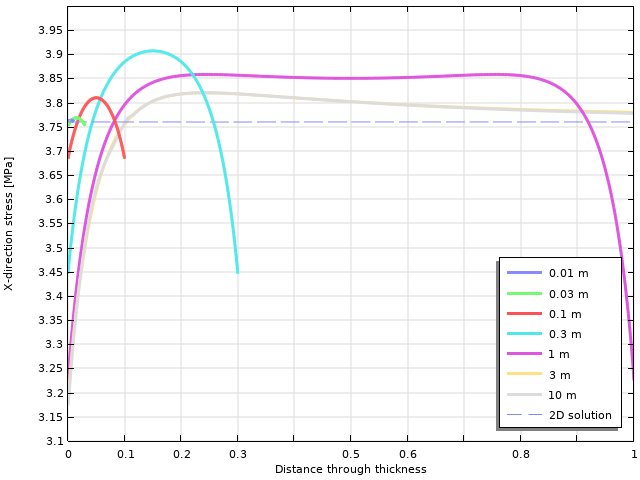
厚さによる水平応力の変化. グラフのパラメーターは, オブジェクトの厚さです.
ご覧いただけるように, 厚さによって大きな変動があります. 薄いオブジェクトの場合, 2D値はよく一致しますが, 厚いオブジェクトの場合, 特に自由表面で大きな違いがあります. これは, 同等の応力にも影響を及ぼします.
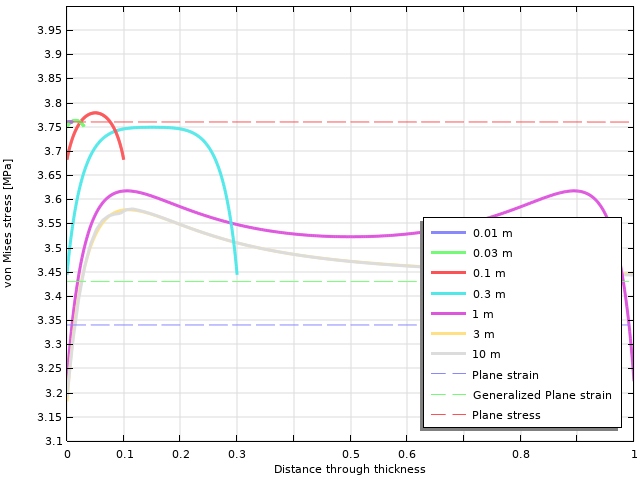
厚さによるフォン・ミーゼス等価応力の変化. グラフのパラメーターはオブジェクトの厚さです.
より厚いオブジェクトの場合, 実際の等価応力と2D解のいずれかとの間に大きな違いがあります. かなり厚いオブジェクトの内部でのみ, フォン・ミーゼス応力は一般化された平面ひずみ解に向かって収束します.
非弾性ひずみ
多くの場合, 3つの定式化の違いは, かなりの応力集中がある前の例ほど顕著ではありません. ただし, 特に注意が必要な場合があります. 非弾性ひずみが重要な場合です. その場合, 横方向に作用するのは, 面内ひずみに対するポアソン比の影響だけではありません.
たとえば, 熱膨張について考えてみます. 通常, すべての方向で均一です. つまり, 面外膨張が抑制される平面ひずみの設定では, 横応力が強く蓄積されます. xy-平面で自由に膨張するオブジェクトには, \sigma_z = -E \alpha \Delta Tの横応力が発生します. 平面応力または一般化された平面ひずみの定式化を使用する場合, 横方向の膨張は自由であり, この応力は表示されません.
熱膨張のケースでの2D定式化の重要性を示すために, 次のケースを検討します. xy-平面で自由膨張する正方形のプレートを, 温度がx*yに比例する温度場にさらします. 最大温度上昇(右上隅)は100Kです. 鋼の材料データが使用されます. 横方向の応力を下図に示します.
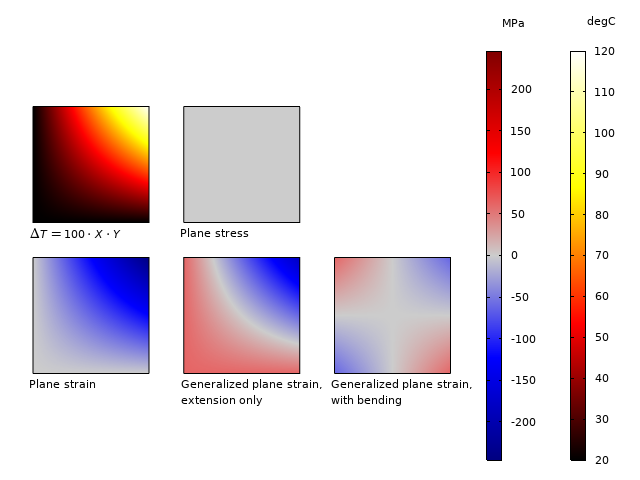
さまざまな2D仮定の温度分布と面外応力\sigma_z.
結果により, 次のことがわかりました.
- 平面応力のケースでは, 面外膨張は自由であるため, 応力は発生しない.
- 平面ひずみのケースでは, セクション全体で圧縮応力が発生し, 値は\sigma_z = -E \alpha \Delta T(x,y)になる. 応力の範囲は-245~0MPa.
- 純粋な伸びを伴う一般化された平面ひずみのケースでは, 一定の応力が追加されるため, 平均(変数)はゼロにる. 応力の範囲は-184~61MPa.
- 曲げを伴う一般化されたひずみのケースでは, 線形に変化する応力場も追加される. 応力は-61~61MPaの範囲.
等価応力に関する注記
最も一般的に使用される2つのスカラー応力測定値は, フォン・ミーゼス等価応力とトレスカ等価応力です. 主応力の観点からそれらを表現すると\sigma_1 > \sigma_2 > \sigma_3, 次のようになります.
そして
ご覧いただけるように, 中間主応力はフォン・ミーゼス等価応力に影響しますが, トレスカ透過応力には影響しません. 2Dの場合, 面外応力成分\sigma_zは常に主要な応力の1つです. 平面応力の場合, それはゼロになります. 平面ひずみのケースでは, それは線形弾性材料の場合は\sigma_z = \nu \left ( \sigma_x + \sigma_y \right ) = \nu \left ( \sigma_{1 \mathrm p} + \sigma_{2 \mathrm p} \right ) です. 最後の式には, 2つの面内主応力が含まれています. \sigma_{1 \mathrm p}と\sigma_{2 \mathrm p}の符号が異なる場合, \sigma_zが常に中間主応力であり, トレスカ等価応力は平面応力と平面ひずみの間の変化の影響を受けません.
この不変の振る舞いは, 中間主応力に依存しているため, フォン・ミーゼス等価応力では見られません.

平面応力と平面ひずみの条件下での等価応力値の差. トレスカ(上)とフォン・ミーゼス(下). トレスカのケースでは, 差がゼロの大きな黒い領域にご注目ください.
破壊力学に関する注記
破壊力学では, 平面ひずみを仮定して厚い板を解析するのが一般的です. ご覧いただいたように, 一般化された平面ひずみまたは完全3Dが正しい選択なのに関わらず, なぜこの方法が使えるのでしょうか?
このコンテキストにおいて, 重要なのは主に亀裂先端の状態です. 亀裂先端のひずみ状態は特異であるため, 材料が厚さ方向に収縮する傾向が強くなります. これに周囲の材料が抵抗して, 厚さ方向の変位に対して強い拘束力を形成します. したがって, 亀裂先端に近い応力状態は平面ひずみに似ています. 実際, 平面ひずみ解と一般化された平面ひずみ解は, 亀裂先端の近くでかなり似たような結果になります. ただし, 平面ひずみが平面亀裂体のどこでも良い近似であるというわけではありません. 実際には, 平面ひずみ解は, グローバルな変形をいくらか過小評価します. プレートのほとんどの部分では, 応力勾配が小さいため, 平面応力の方がより適切な近似値となります.
次のステップ
COMSOL Multiphysics のアドオンである構造力学モジュールは, 平面応力と平面ひずみをモデル化するための特殊な機能を備えています. 下のボタンをクリックして, モジュールの詳細をご覧ください.


コメント (0)