
多くのエンジニアリングの状況では, 対象系の励起と応答は時間の経過とともに正弦波になると想定できます. この想定が成り立つ場合, いわゆる周波数領域解析を使用できます. これにより, 非常に効率的な解法がいくつか得られます. この想定を行える基本的な概念と条件をいくつか確認しながら, さまざまな求解アプローチを検討してみましょう.
エンジニアリングと科学における時間調和負荷
固体力学, 音響学, 電磁気学… これらは, 正弦波励起があると想定できるエンジニアリング分野のほんの一部です. たとえば, 車のホイールのバランスが崩れると, 時間とともに変化する正弦波状の力が生じ, ホイールの回転と同じ周波数で車両の構造が振動します. 音響学では, スピーカーの膜が1つまたは複数の周波数で駆動され, 同じ周波数の音波が放射されます. 同様に, 電磁気学では, 送電線は一定の周波数で動作します. 携帯電話のアンテナは, 離散的な周波数範囲にわたって電磁波を放射し, レーザーはほぼ単色の単一周波数の光を出力します. まったく異なる分野に関連しているにもかかわらず, これらの各ケースで知っておく必要のあるモデリング手法は驚くほど似ています.

左: バランスの取れていないタイヤは, 時間調和負荷が発生する可能性がある1つの例にすぎません. 画像は CC BY 2.0 のライセンスを受けており, Flickr Creative Commons から提供されています. 右: 車のリムのトリムウェイト.
これらのさまざまなケースを支配する偏微分方程式はすべて, 同じ一般的な形式を持っています:
(1)
M u_{tt} + C u_t + \nabla \cdot (-K \nabla u) = F &\text { on } \Omega \\
\mathbf{n} \cdot (K \nabla u) + Au = f &\text{ on } \Gamma_1 \\
u = g &\text{ on } \Gamma_2
\end{align}
ここで, u=u(\mathbf{x},t) は, 空間および時間によって変化する関心領域です (構造問題の場合は変位, 音響問題の場合は圧力など). M, K, C の項は, 異なる材料特性を表し, 通常はそれぞれ質量, 剛性, 減衰項と呼ばれます. F=F(\mathbf{x},t) の項は, 領域上の分布荷重を表します. また, 系上の荷重 f=f(\mathbf{x},t) と制約 g=g(\mathbf{x},t) を表す境界条件のセットも常に存在します. 境界荷重は, ロビン境界条件によって指定されます. この条件には, 境界吸収または境界インピーダンスがゼロになる可能性があることを示す項 A が含まれます. これらの荷重 f と制約 g は, ゼロ (均質) または非ゼロ (非均質) の境界条件になります.
上記の式の最も単純なケース, つまり, 下の図に示す単純な調和振動子を見てみましょう.
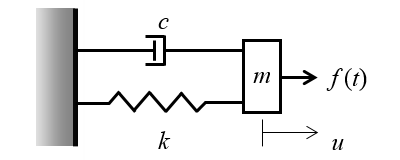
単振動子では, バネとダンパーによって質量が剛体壁に接続されています. 時間とともに変化する力を加えると, 質量が前後に振動します.
ここで, 初期条件 u(\mathbf{x},t=0)=u_0 も設定すれば, この系の変位応答を時間経過とともに計算できます. 下のグラフは, 荷重 f(t)=\sin(\omega t) と初期条件 u_0=0 が適用された場合の質量の変位を示しています. これらの条件下では, 質量はゼロから前後に振動し始めます. 初期の起動時間が経過すると, 変位は周期的になります. つまり, 一定の角周波数 \omega で正弦波状に繰り返され, 初期条件に依存しなくなります.
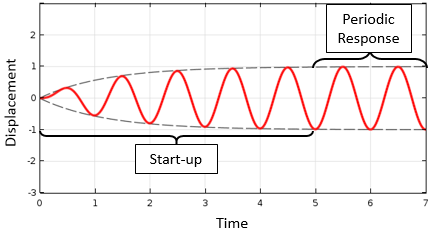
正弦波励起に対する単調振動子の応答. 初期条件がゼロから始まり, 変位は最終的に時間的に周期的になります.
ここには, 実際に必要なデータよりもはるかに多くのデータがある可能性があります. たとえば, 起動期間中の時間変化ではなく, 起動時間の合計のみに関心がある場合があります. さらに, 起動期間後は, 変位の大きさのみに関心がある場合があります. したがって, 時間領域でこのような問題を解くことは実際には必要ではありません. 代わりに, これをいわゆる周波数領域問題に変換することができます.
ただし, 周波数領域解析は, 2つの重要な仮定に依存しています. 1つ目は, 系上のすべての時間変動負荷と制約が同じ固定周波数で正弦波状に変化する必要があることです. 2つ目は, すべての負荷, 制約, および材料特性が解から独立している必要があることです. この2つの仮定の下では, 解は次の形式を取ると推測できます:
これは時間に関して微分でき, 元の支配的な偏微分方程式に代入すると, 次のようになります:
(2)
-\omega^2 M \tilde u + j \omega C \tilde u+ \nabla \cdot (-K \nabla \tilde u) = \tilde F & \text { on } \Omega \\
\mathbf{n} \cdot (K \nabla \tilde u) + A \tilde u = \tilde f &\text{ on } \Gamma_1 \\
\tilde u = \tilde g &\text{ on } \Gamma_2
\end{align}
これは, 支配方程式の周波数領域形式を提供します. 場は複素数値になるため, 解の振幅と位相に関する情報が含まれていることに注意してください. この偏微分方程式と境界条件は線形であるため, 線形静的有限要素モデルの求解に関する以前のブログで説明したように, 非常に簡単に解くことができます. 次に, これらのタイプの問題に対するさまざまな求解手法についてさらに詳しく見ていきましょう.
周波数領域での問題の分析
COMSOL Multiphysics® ソフトウェアには, 上記の方程式 (式 (2)) を解くのに適したさまざまなアルゴリズムが含まれています. 最も簡単なアプローチは周波数領域ソルバーです. このソルバーは, 入力として, シミュレーションする単一の周波数または離散的な周波数範囲を受け取ります.
たとえば, 前述の単純な調和振動子の問題をさまざまな励起周波数で解くと, 以下に示すようなプロットが得られます. これは, さまざまな励起周波数の変位量を示しています. 関連する物理に関係なく, 周波数応答は常に以下の曲線に似ています. 応答対周波数曲線には, 系の共振周波数に対応する最大値があります. この最大値の両側の応答は低下し, 最大値の半分での全幅の帯域幅を使用して, 品質係数である Q を計算できます. 品質係数は, 前述の系の起動時間に関連できるため, 特に便利です.
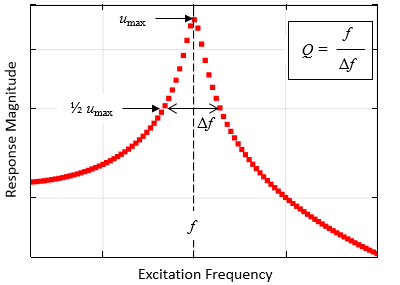
一連の離散周波数で解いた, 周波数領域における正弦波負荷に対する調和振動子の応答を表すプロット. このようなプロットから, 共振周波数と品質係数を推定できます.
周波数領域ソルバーを使用してこのような問題を解く場合, COMSOL Multiphysics ソフトウェアは指定された励起周波数ごとに順番に解を出します. したがって, 解く周波数の数に比例して, 解の時間が長くなります. 解の時間を短縮するには, フローティングネットワークライセンスで使用できるクラスタースイープオプションと, 漸近波形評価 (AWE) ソルバーの2つの方法があります.
クラスタースイープオプションを使用すると, ソフトウェアは周波数のリストを個別の範囲に自動的に分割します. これらの範囲のそれぞれは, クラスター上の異なる計算ノードで解かれます. ここでの利点は, 必要な数のクラスターノードを使用して, 計算を大幅に並列化できることです. モデルを設定して, 周波数範囲ごとに異なるメッシュを使用することもできます. これは, 非常に広帯域の励起がある場合に有利な要素です. ソフトウェアは, クラスターのさまざまなノードで計算された解をつのモデル内に自動的に再組み立てします. 以下のプロットは, 周波数スイープが区間に分割され, クラスターの異なるノードで解かれる様子を示しています. COMSOL ブログ クラスターコンピューティングの詳細 をご覧ください.
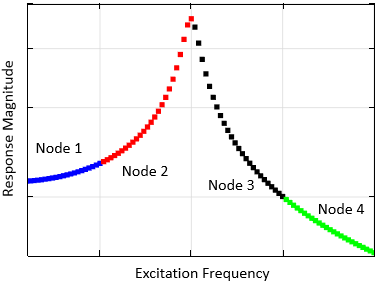
前と同じ周波数スイープですが, クラスターの異なるノードで異なる周波数範囲が解かれています.
ソルバーを使用すると, ソフトウェアは対象の周波数範囲を検索し, 区間内の離散周波数で計算ポイントを連続して追加して, 応答対周波数曲線の良好な解像度を取得します. このアプローチは, 以下のプロットに示されています. AWE ソルバーが共振点付近のポイントをより多く求解し, 応答が周波数とともに徐々に変化するポイントをより少なく求解する様子に注目してください. このようなアプローチは, クラスタースイープオプションと組み合わせることができます.
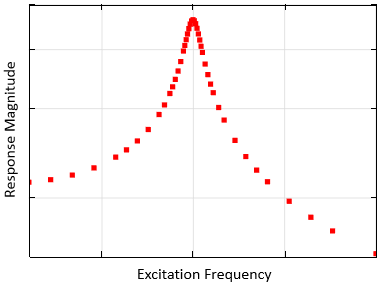
ソルバーは, 応答が周波数によって大きく変化する範囲に追加の計算ポイントを導入します.
これまでに説明したすべての求解アプローチでは, 求解時間要件は異なりますが, 同様の応答曲線が得られます. これらの解は, さまざまな励起周波数で系がどのように応答するかを理解するのに役立ちます. 前述のように, このような曲線を使用して, 系の共振周波数と品質係数を推定することもできます. 実際, これらが唯一の2つの量である場合もあります. ここで, 固有周波数ソルバーと呼ばれる別の解アプローチについて説明します.
固有振動数の問題を解くとき, ソフトウェアは実際には, 前述の支配的な偏微分方程式で記述されたモデルとは若干異なるモデルを解いています. 共振の固有振動数に関心があるため, すべての非同次荷重と制約は同次 (ゼロ振幅) 形式に変更されます:
(3)
-\omega^2 M \tilde u + j \omega C \tilde u+ \nabla \cdot (-K \nabla \tilde u) = 0 & \text { on } \Omega \\
\mathbf{n} \cdot (K \nabla \tilde u) + A \tilde u = 0 &\text{ on } \Gamma_1 \\
\tilde u = 0 &\text{ on } \Gamma_2
\end{align}
この形式の支配方程式を解くと, 系のいわゆる固有値, \lambda = -j \omega + \delta が計算されます. これらの複素数値の固有値から, 共振周波数, f=\omega/2\pi, および品質係数, Q=f/2\delta が得られます. 複素数値の固有値は, 系内の損失, つまりゼロでない減衰項 C, または複素数値の質量 M, 剛性 K, または吸収 A 項によって発生します. 損失がない場合, 品質係数は無限大となり, ソフトウェアは共振周波数のみを返します. また, 場の解 \tilde u も返されます. これを使用して, 共振時の系の動作を可視化できます. この解は, モード形状または固有モードと呼ばれることがよくあります.
非常に単純な構造問題 (両端が固定された細い梁) の固有周波数解析のサンプル結果を見てみましょう. 梁の面内曲げモードの共振周波数とモード形状を下にプロットします.
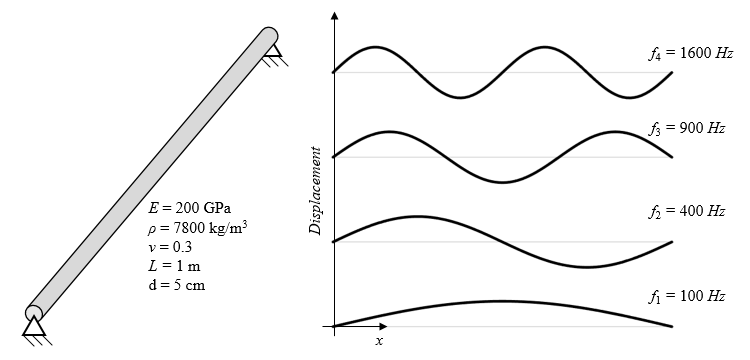
ピン留めされた円形ビームの最初の4つの共振周波数とモード形状.
これらの固有値の結果は, 実際には, 周波数領域モーダルスタディと呼ばれる別のスタディタイプで使用できます. これは, いわゆる2段階スタディです. 最初のスタディステップでは, ユーザーが指定した数の固有周波数とモード形状が計算されます. 2番目のステップでは, これらの固有値解の線形結合を使用して, 周波数応答動作を再構築します. このアプローチは, 使用する固有値が多いほど正確になります. これは, 周波数領域ソルバーを使用したスイープと, 関与する固有値の数が異なる周波数領域モーダルソルバーの結果を比較した以下のプロットで確認できます.
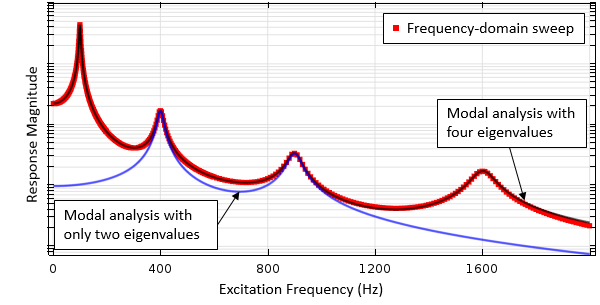
周波数領域スイープと, 異なる数の固有値を使用した周波数領域モーダルスタディの比較.
線形系の調和励起のモデリングに関するまとめ
線形系の調和励起のモデリングは, 多くの解析問題において重要なステップです. 今回は, COMSOL Multiphysics がそのようなモデルを解くために提供するさまざまな解アルゴリズムを紹介しました. モデルによってメリットが異なるため, これらの手法をすべて覚えておく必要があります.
しかし, 非線形系についてはどうでしょうか. これらの系は, 低次高調波や高次高調波の生成など, 調和励起に対して非常に異なる反応を示します. 今後のブログで取り上げる予定のとおり, これらの複雑なケースに対処するために使用できる強力なツールが数多く用意されています. お楽しみに!
線形系の調和励起のモデリングのさまざまなアプリケーションを調べる
- COMSOL Multiphysics で線形系の調和励起のモデリングを自分で試してみませんか? このチュートリアルのリストを参照して, エンジニアリングの焦点に最も適したものを見つけてください:
- エルボーブラケットのさまざまな解析, 周波数領域, 固有周波数, 周波数領域モーダル解析を特徴とする構造力学チュートリアル
- さまざまな周波数領域ソルバーで解析したヘルムホルツ共振器, 周波数領域, 固有周波数, 周波数領域モーダル解析を含む音響チュートリアル
- RF コイル, 波動周波数領域および固有周波数解析を特徴とする電磁気学チュートリアル
- エバネッセント モード円筒キャビティフィルター, 周波数領域および AWE 解析を含む波動電磁気学の例
- カスケード長方形キャビティフィルター, 周波数領域および周波数領域モーダル AWE 解析を特徴とする波動電磁気学チュートリアル
- 関連ブログを読む: バンドパスフィルタータイプのモデリングを高速化するメソッドデバイス
- このトピックに関してさらにご質問がありますか? お気軽にお問い合わせください. 今すぐお問い合わせください





コメント (0)