Menu
COMSOL ブログ

構造力学における減衰: 理論と原因

Author Image
Henrik Sönnerlind 著
2019年 3月 14日

ガラスや金属でできたボウルを叩くと, 時間の経過とともに減衰する強度の音が聞こえます. 減衰のない世界では, 音は永遠に残ります. 実際には, ボウル内の運動エネルギーと弾性エネルギーが他のエネルギー形式に消散する物理的なプロセスがいくつかあります. このブログでは, 減衰の表現方法と, 振動する構造で減衰を引き起こす物理的現象について説明します.

減衰はどのように定量化されるのか?

数学的な観点から減衰を説明する方法はいくつかあります. より一般的な説明のいくつかを以下にまとめます.

減衰の最も明らかな兆候の1つは, シンギングボウルの場合のように, 自由振動中の振幅の減衰です. 減衰率は減衰の大きさによって異なります. 振動振幅が時間とともに指数関数的に減少するのが最も一般的です. これは, サイクル中に失われるエネルギーがサイクル自体の振幅に比例する場合です.

典型的なシンギングボウルの写真.
典型的な “シンギングボウル”. 画像提供: Sneharamm0han — 自身の作品. CC BY-SA 4.0 ライセンス, Wikimedia Commons 経由.

まず, 粘性減衰があり外部荷重のない1自由度 (DOF) の系の運動方程式から始めましょう.

m \ddot u + c \dot u + k u = 0

質量 m で割ると, 正規化された形式が得られます. 通常は次のように記述されます.

\ddot u + 2 \zeta \omega_0 \dot u + \omega_o^2 u = 0

ここで, \omega_0 は減衰のない固有振動数で, \zeta は 減衰率 と呼ばれます.

動作が周期的であるためには, 減衰率は 0 \le \zeta < 1. の範囲に制限される必要があります. この系の自由振動の振幅は, 次の係数で減衰します

e^{-\zeta \omega_0 t} = e^{\frac{-2 \pi \zeta t }{T_0}}

ここで, T0 は減衰のない振動の周期です.

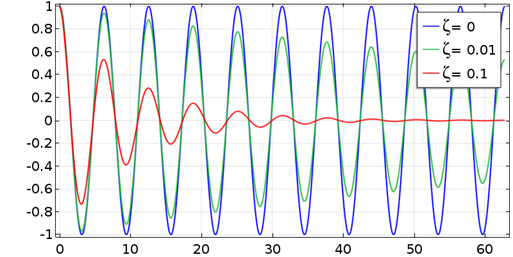
減衰系における自由振動減衰のグラフ.
減衰比の3つの異なる値に対する自由振動の減衰.

使用されているもう1つの尺度は, 対数減衰, δ です. これは, 2つの連続するピークの振幅の比の対数です.

\delta = \mathrm {ln} \left ( \dfrac{u(t_i)}{u(t_{i+1})} \right ) = \mathrm {ln} \left ( \dfrac{u(t_i)}{u(t_i+T)} \right )

ここで, T は周期です.

対数減衰率と減衰率の関係は, 次のとおりです

\delta = \dfrac{2 \pi \zeta}{\sqrt{1-\zeta^2}} \approx 2 \pi \zeta

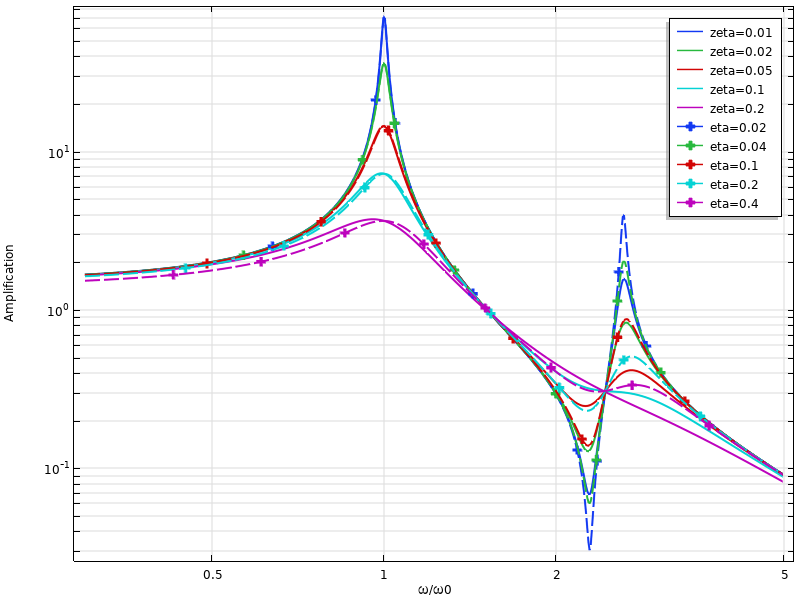
減衰の効果が重要な役割を果たすもう1つのケースは, 構造が自然周波数に近い周波数で高調波励起を受ける場合です. 共振時に, 系に何らかの減衰がない限り, 振動振幅は無限大に近づきます. 共振時の実際の振幅は, 減衰の量によってのみ制御されます.

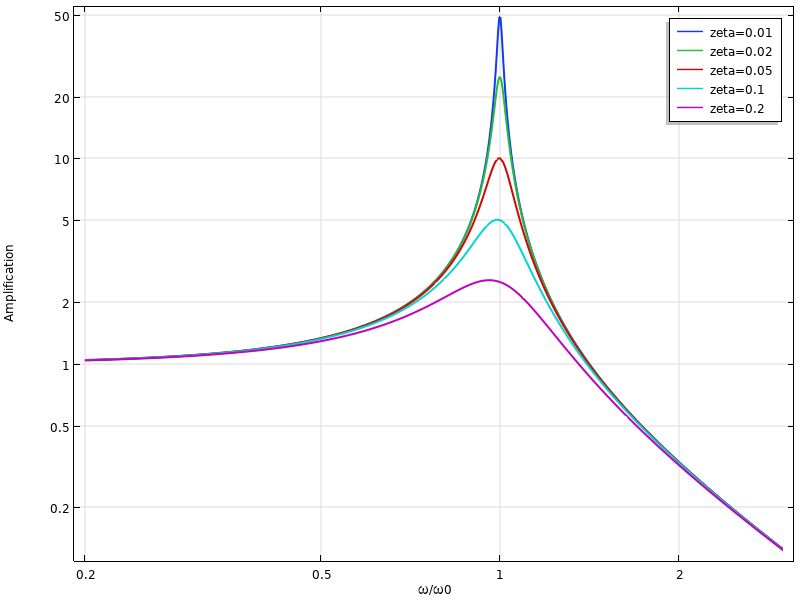
単一自由度減衰系における増幅のプロット.
異なる周波数と減衰率での単一自由度系の増幅.

共振器などの一部の系では, 可能な限り増幅を得ることが目的です. これにより, 別の一般的な減衰測定である 品質係数 または Q 係数 が生まれます. これは, 共振時の増幅として定義されます. Q 係数は, 減衰率と次の式で関連しています

Q = \dfrac{1}{2 \zeta \sqrt{1-\zeta^2}} \approx \dfrac{1}{2 \zeta}

減衰の説明のもう1つの出発点は, 加えられた力と結果として生じる変位, または応力とひずみの間に一定の位相シフトがあると仮定することです. 位相シフトについて話すことは, 定常状態の調和振動に対してのみ意味があります. 完全な期間にわたって応力とひずみをプロットすると, ヒステリシスループ を表す楕円が表示されます.

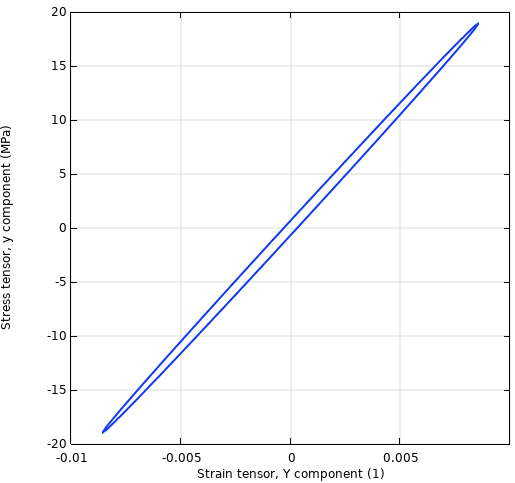
COMSOL Multiphysics の応力-ひずみ履歴のプロット.
応力-ひずみ履歴.

材料特性は複素数値であると考えることができます. したがって, 一軸線形弾性の場合, 複素数値の応力-ひずみ関係は次のように記述できます

\tilde \sigma = \tilde E \tilde \varepsilon = (E^\prime+iE^{\prime \prime}) \tilde \varepsilon

ここで, ヤング率の実部は 貯蔵弾性率 と呼ばれ, 虚部は 損失弾性率 と呼ばれます. 多くの場合, 損失弾性率 は損失係数 η で記述されるため

\tilde E = E(1+i \eta)

ここで, E は貯蔵弾性率 E’ として識別できます. また, 別の定義に遭遇することもあります. その定義では, E は応力振幅とひずみ振幅の比です. したがって,

E = |\tilde E| = \sqrt{(E^\prime)^2+(E^{\prime \prime})^2}

この場合

\tilde E = \dfrac{E(1+i \eta)}{\sqrt{1+\eta^2}}

この区別は, 損失係数の値が高い場合にのみ重要です.

損失係数減衰の同等の尺度は, 次のように定義される 損失正接 です

\mathrm {tan} \, \delta = \dfrac{E^{\prime \prime}}{E^\prime} = \eta

損失角 δ は, 応力とひずみの間の位相シフトです.

損失係数によって定義される減衰は, 粘性減衰とは多少異なる動作をします. 損失係数減衰は変位振幅に比例しますが, 粘性減衰は速度に比例します. したがって, 一方の数値を他方の数値に直接変換することはできません.

下の図では, 単一自由度系の応答を2つの減衰モデルで比較しています. 粘性減衰は, 共振より上では損失係数減衰よりも高い減衰を予測し, 共振より下では低い減衰を予測することがわかります.

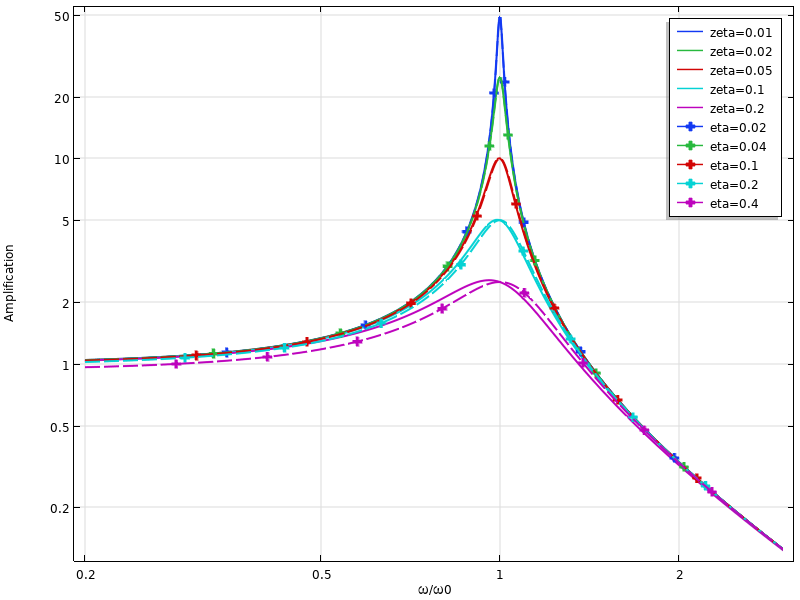
粘性減衰と損失係数減衰の動的応答を比較したプロット.
粘性減衰 (実線) と損失係数減衰 (破線) の動的応答の比較.

通常, 減衰比と損失係数減衰の変換は, 共振周波数で考慮され, 次に \eta \approx 2 \zeta で考慮されます. ただし, これは単一の周波数でのみ当てはまります. 下の図では, 2 DOF 系が考慮されます. 減衰値は最初の共振で一致しており, 2番目の共振での予測が大幅に異なることは明らかです.

2 DOF 系の動的応答を比較するプロット.
2 DOF 系の粘性減衰と損失係数減衰の動的応答の比較.

損失係数の概念は, 損失係数をエネルギーの観点から定義することで一般化できます. 上記の材料モデルの場合, 負荷サイクル中に消費されるエネルギーは, 次の式で表されます

D = \pi E^{\prime \prime} \varepsilon_a^2

ここで, \varepsilon_a はひずみ振幅です.

同様に, サイクル中の最大弾性エネルギーは

W_s = \dfrac{1}{2} E^{\prime} \varepsilon_a^2

したがって, 損失係数はエネルギーで次のように表すことができます

\eta = \dfrac{E^{\prime \prime}}{E^\prime} = \dfrac{D}{2 \pi W_s}

散逸エネルギーに関するこの定義は, ヒステリシスループが実際に完全な楕円であるかどうかに関係なく使用できます. ただし, 2つのエネルギー量が決定できる限りです.

減衰の原因

物理的観点から見ると, 減衰の原因は多数考えられます. 自然は常にエネルギーを消散させる方法を見つけようとする傾向があります.

材料の内部損失

実際の材料はすべて, ひずみを受けるといくらかのエネルギーを消散します. これは一種の内部摩擦と考えることができます. 完全な負荷サイクルの応力-ひずみ曲線を見ると, 完全な直線を描くことはありません. むしろ, 細い楕円のようなものが見られます.

多くの場合, 損失係数減衰は材料減衰の適切な表現と考えられています. これは, 経験上, サイクルあたりのエネルギー損失は周波数と振幅にほとんど依存しない傾向があるためです. ただし, 損失係数減衰の数学的基礎は複素数値に基づいているため, 基本的な仮定は調和振動です. したがって, この減衰モデルは周波数領域解析にのみ使用できます.

材料の損失係数は, その詳細な構成や参照する情報源によって大きく異なります. 下の表に, 大まかな推定値を示します.

材料 損失係数, η
アルミニウム 0.0001 ～ 0.02
コンクリート 0.02 ～ 0.05
銅 0.001 ～ 0.05
ガラス 0.0001 ～ 0.005
ゴム 0.05 ～ 2
スチール 0.0001 ～ 0.01

損失係数や同様の減衰の説明は, 主に材料の減衰の正確な物理特性が不明または重要でない場合に使用されます. 粘弾性などのいくつかの材料モデルでは, 散逸はモデルの固有の特性です.

ジョイントの摩擦

構造物は, ボルトやリベットなどで接合されるのが一般的です. 振動中に接合面が互いに滑っている場合, エネルギーは摩擦によって消散します. 摩擦力の値自体がサイクル中に変化しない限り, サイクルごとに失われるエネルギーは, 多かれ少なかれ周波数に依存しません. この意味で, 摩擦は材料の内部損失に似ています.

ボルト接合は機械工学でよく使用されます. ボルト接合で発生する消散量は, 設計によって大きく異なります. 減衰が低いことが重要である場合は, 接合面間のマクロ的な滑りが起こらないように, ボルトの間隔を狭くしてしっかりと締める必要があります.

音の放出

振動する表面は周囲の空気 (または周囲の他の媒体) を移動させ, 音波を放出します. これらの音波はエネルギーの一部を運び去り, 構造の観点からはエネルギー損失となります.

Tonpilz トランスデューサーの音放出の可視化.
Tonpilz トランスデューサーの音放出のプロット.

アンカー損失

多くの場合, 小さな部品は, シミュレーションの一部ではない大きな構造に取り付けられています. 部品が振動すると, いくつかの波が支持構造に誘導され, 運び去られます. この現象は, 特に MEMS に関しては, しばしば アンカー損失 と呼ばれます.

熱弾性減衰

散逸のない純粋な弾性変形の場合でも, 材料にひずみを与えると温度がわずかに変化します. 局所的な伸張は温度低下を招き, 圧縮は局所的な加熱を意味します.

基本的に, これは可逆的なプロセスであるため, 応力が解放されると温度は元の値に戻ります. ただし, 通常は応力場には勾配があり, それに応じて温度分布にも勾配があります. これにより, 暖かい領域から冷たい領域への熱流束が発生します. 負荷サイクルの後半で応力が除去されると, 温度分布は負荷によって生じたものと同じではなくなります. したがって, 局所的に元の状態に戻ることはできません. これが散逸の原因になります.

熱弾性減衰効果は, 長さスケールが小さく, 高周波振動を扱う場合に最も重要です. MEMS 共振器の場合, 熱弾性減衰によって Q 係数が大幅に低下する可能性があります.

ダッシュポット

構造物には, 車輪サスペンションのショックアブソーバーのように, 意図的に個別のダンパーが含まれている場合があります.

ショックアブソーバーの写真.
ショックアブソーバー. 画像提供: Avsar Aras — 自作. CC BY-SA 3.0 ライセンス, Wikimedia Commons 経由.

このような部品は, 少なくとも一部の振動モードに関しては, 構造全体の減衰に大きな影響を与えることは明らかです.

地震ダンパー

減衰に多大な労力が費やされる特定のケースは, 地震活動が活発な地域の土木構造物です. 地震に見舞われた場合, 建物の振動レベルを下げることが最も重要です. このようなダンパーの目的は, 構造物を基礎から分離することと, 減衰を提供することの両方です.

建物の地震ダンパーの写真.
市営ビルの地震ダンパー. 画像は Shustov 氏によるもので, 自身の作品です. CC BY-SA 3.0 ライセンス, Wikimedia Commons 経由.

その他の資料

このブログの続編はこちらでお読みください:

コメント (0)

コメントを残す
ログイン | 登録
Loading...
COMSOL ブログを探索
カテゴリー
タグ