COMSOL Multiphysics® ソフトウェアバージョン 6.0 では, AC/DC モジュール内の磁場 (電流のみ) インター フェースの機能を拡張し, 非磁性材料からなる電気系の定常および周波数依存のインダクタンス行列と交流抵抗を計算できるようになりました. これは, プリント回路基板やパワーバスシステムの解析に役立ちます. ただし, 部分インダクタンスの解釈と適切な利用には, 少し理解する必要があります. では, 学んでいきましょう!
全インダクタンスと部分インダクタンスの定義と計算
全インダクタンスと部分インダクタンスを理解するために, まず下図のような正方形のループ状のワイヤーをモデルに考えてみましょう. この閉ループに沿って電流が流れると, 周囲の空間に磁場が発生します. モデル空間に蓄積された磁気エネルギーの総和 W_{m}^{tot} とコイルに流れる電流 I から, L^{tot} = 2 W_m^{tot}/I^2 を介して, 全インダクタンス L^{tot} (単にインダクタンスと呼ばれることが多い) を定義し, 計算することができます. 線径1 mm, 一辺長2 cm のこの正方形ループの全インダクタンスは50.6 nH です.
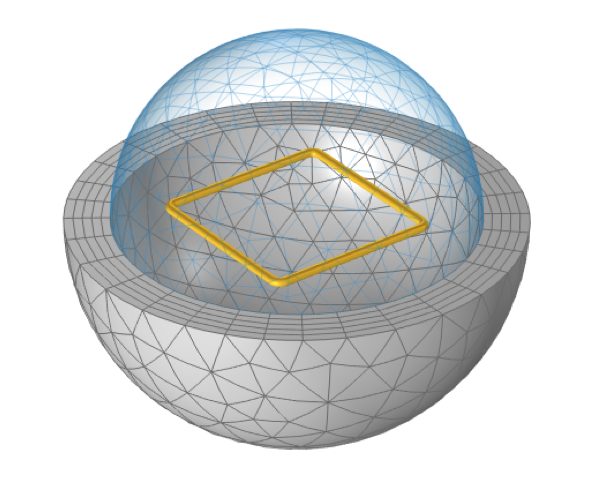
無限要素ドメインでトランケートされた球形の自由空間ドメイン内にある正方形のワイヤーのループは, 定義された全インダクタンスを持ちます.
このモデルは, 無限要素でトランケートされた球状ドメインを使用しています. 全体的なモデリングアプローチは, アプリケーションギャラリのヘルムホルツコイルの例と非常によく似ています. この例では, 磁場 (電流のみ) インターフェースと磁場インターフェースの両方を使用しており, これらの定式化で同一の結果が得られることを示しています.
磁場 (電流のみ) インターフェースと磁場インターフェースはどちらも使用できますが, この2つの定式化には多くの違いがあります. ここでは, 磁場 (電流のみ) のインターフェースを特徴づける3つの点に絞って説明します:
- インダクターコアなどの透磁率の高い材料が存在しないことを条件とする.
- すべての導体が体積を持つものとしてモデル化されている必要がある.
- 全インダクタンスだけでなく, 部分インダクタンスも計算できる.
丸線の空芯ループのモデルは, 最初の2つの要件を明らかに満たしているので, 3番目のポイントである: 部分インダクタンスの計算に焦点を当てましょう.
全インダクタンスの概念は, 常に電流の完全なループを必要としますが, 部分インダクタンスの背後にある考え方は, 全体のループを複数の部分に細分割し, それぞれが部分的な自己インダクタンスと部分的な相互インダクタンスを寄与するようにすることです. これらの寄与を重ね合わせることで, 閉ループの全インダクタンスが算出されます. 理論的にもモデリング的にも, この細分割の方法は自由自在であり, 工学的な目的に最も適した方法をとることができます.
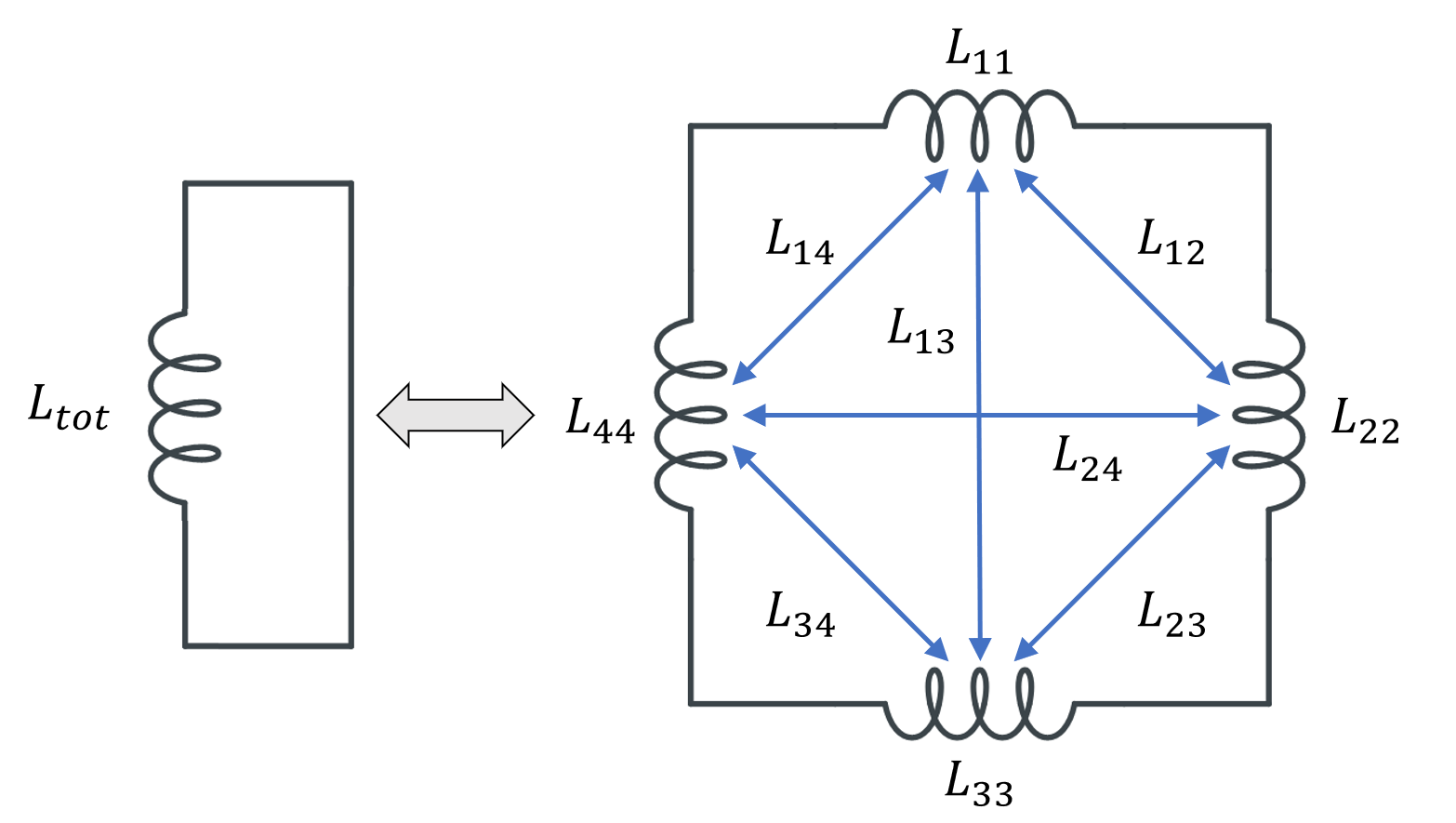
1つのインダクターを4分割し, 4つの部分自己インダクタンスと12個の部分相互インダクタンスを持たせたもの. 対称性の理由から, 後者のうち6つにのみ名前が付けられています.
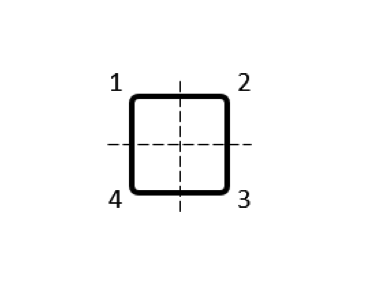
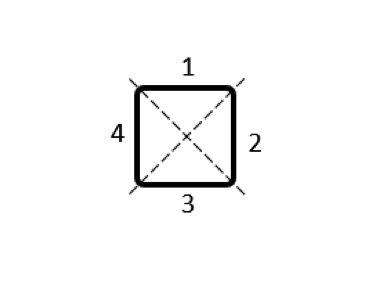
導体体積を細分割するためのいくつかの異なる方法を以下の表に示します. モデリングに関しては, これらのドメインのそれぞれについて, 別の導体機能を使用し, 各ドメインの両端に端子と接地の境界条件を設定し, 電流が常にループの周囲を同じ方向に流れるように選択します. ここで得られる出力は部分インダクタンスの行列です. この行列の数値に注目してみましょう. 行列の対角線上の項を部分自己インダクタンス, 対角線外の項を部分相互インダクタンスと呼びます.
| コイル細分割 | 部分インダクタンス行列 (nH) |
|---|---|
|
\begin{bmatrix}11.84 & 0.85 & -0.89 & 0.85\\0.85 & 11.84 & 0.85 & -0.89\\-0.89 & 0.85 & 11.84 & 0.85\\0.85 & -0.89 & 0.85 & 11.84\\\end{bmatrix} |
|
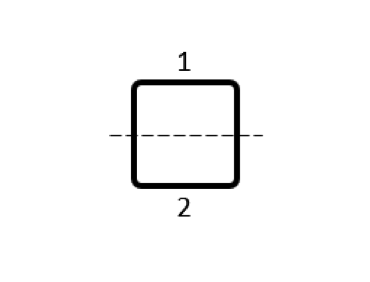
\begin{bmatrix}14.0 & 0.2 & -1.75 & 0.2\\0.2 & 14.0 & 0.2 & -1.75\\-1.75 & 0.2 & 14.0 & 0.2\\0.2 & -1.75 & 2& 14.0\\\end{bmatrix} |
|
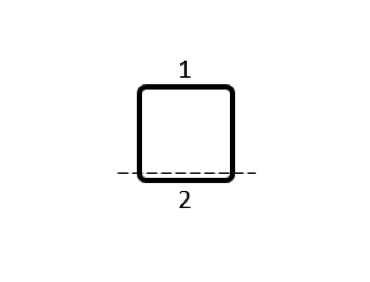
\begin{bmatrix}25.38 & -0.08 \\-0.08 & 25.38 \\\end{bmatrix} |
|
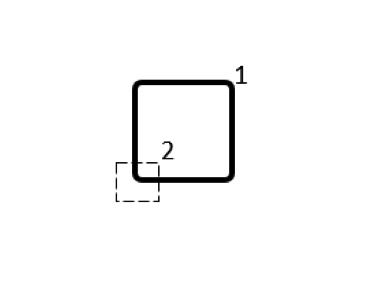
\begin{bmatrix}38.4 & -1.3 \\-1.3 & 14.8 \\\end{bmatrix} |
|
\begin{bmatrix}49.3 & 0.5 \\0.5 & 0.3 \\\end{bmatrix} |
コイルの細分割のさまざまな選択に対する部分インダクタンス行列の表. 行列項の和は常に同じです.
なお, 部分自己インダクタンスは常に正であり, この場合, 正にも負にもなりうる部分相互インダクタンスのどれよりもはるかに大きいことに注意してください. すべての行列項の総和は, 全インダクタンスに等しくなります: L^{tot} = \sum_{i,j}L_{ij} これは, コイルの細分割の仕方に関係なく成立します. しかし, 細分割の仕方が異なると, 部分インダクタンス行列は, 自己インダクタンスによってより大きく支配される可能性があります.
コイルの特定の細分割がより対角線上に支配的な部分インダクタンス行列につながるというこの観察に基づいて, 自由空間にあるコイルの1セクションのみのサブモデルを構築することが正当化されます (下図に表示, 上の表の最初の細分割に対応). このモデルは, 端子と接地の条件を両端に持つ, 単一の導体ドメインを使用しており, 11.84 nH の部分自己インダクタンスという単一の量だけを出力します. これは, 先に計算した部分インダクタンス行列の対角項と等しくなります.
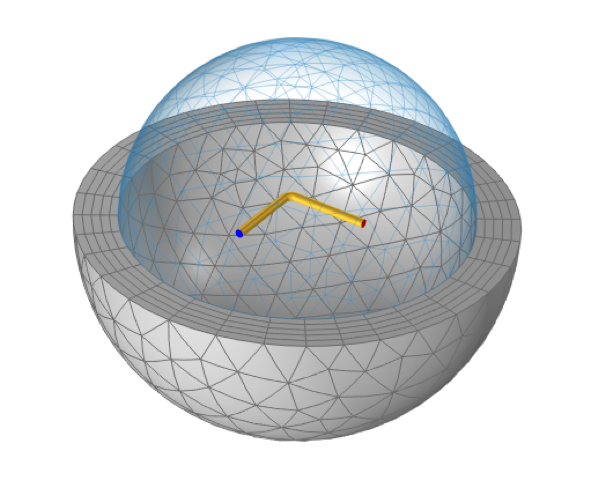
正方形ループの4 分の1のモデルで部分自己インダクタンスを計算することができ, この場合, インダクタンスを適切に予測することができます. 磁場 (電流のみ) インターフェースでは, 自由空間で終端するコイルを使用でき, 両端に端子と接地の条件があります.
さて, このモデルはワイヤーの端 (端子と接地の境界条件が適用されているところ) で電流を作ったり壊したりしているように見えますが, これが磁場 (電流のみ) インターフェースの特徴です. このインターフェースは, 閉ループで接続されていない場合でも, 導電性ドメインのセットの部分自己インダクタンス (および部分相互インダクタンス) を計算することができるのです.
次の例では, コイルの2番目の細分割を見ていきましょう. この細分割では, 以下の表に示されている, 丸線の短い直線部分を見ることができますが, ハンドブック解があるため, これは特に興味深いケースです. この場合, 表皮深さが直径よりはるかに大きい低周波から, 表皮深さがはるかに小さい高周波までの周波数範囲におけるインダクタンスと交流抵抗を見ていきます. このため, 表皮効果を解消するために, 境界層メッシュを使用する必要があります. また, 無限要素ドメインの使用を省略し, 球状のモデリング空間の境界にはデフォルトの外部境界条件を使用します. この条件は, モデル内の電流の流れに基づいた近似的な境界条件を適用するため, 計算ドメインの半径を調べる必要があります.
| 丸線の交流インダクタンスと抵抗のハンドブック値 | |
|---|---|
| 低周波インダクタンス | \frac{\mu_0}{2\pi}\ell\left[ \ln\left( \frac{2\ell}{r}\right) -\frac{3}{4}\right] |
| 高周波インダクタンス | \frac{\mu_0}{2\pi}\ell\left[ \ln\left( \frac{2\ell}{r}\right) -1\right] |
| 直流抵抗 | \frac{\ell}{\sigma \pi r^2} |
| 交流抵抗 | \frac{\ell}{\sigma \pi (2r\delta – \delta^2)} |
| 長さ: \ell, 半径: r,電気伝導率: \sigma, 表皮深さ: \delta =\sqrt{ \frac{2}{\omega \mu_0\sigma}} | |
計算結果は, 直流抵抗が完全に一致し, 低周波インダクタンスもほぼ一致 (1 % 以内) しています. 低周波で若干の不一致があるのは, 端効果によるもので, 直線ワイヤーの場合, 数値モデルとハンドブックの値の一致は, 長さが長いほどよくなることが解析で確認されています.
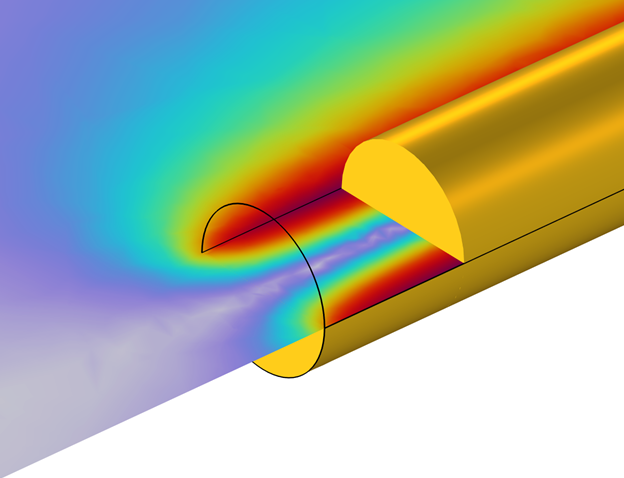
ワイヤー内部の切断面クローズアップ図. 計算された磁場は端効果を表示.
交流抵抗も広い範囲で良い一致を示しているが, 表皮深さが線径よりもはるかに小さい高周波では, 顕著な偏差が見られます. この偏差は, 別の問題によるものです: このような高周波数では, 表皮効果を解消するために非常に細かい境界層メッシュが必要になるのです.
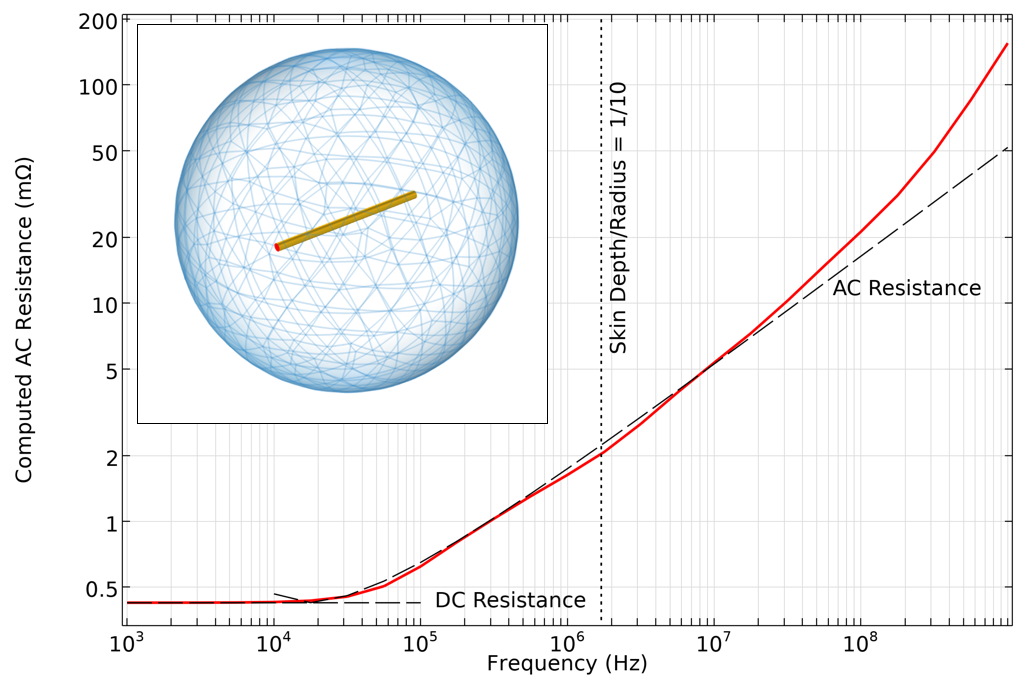
直線ワイヤーの交流抵抗を計算し, 表皮深さに基づくハンドブック式と比較したもの. 非常に高い周波数では, 非常に細かいメッシュが必要となり, 変位電流が無視できるという仮定はもはや成り立たなくなります.
このように周波数が高くなると, また別の問題が出てきます: 近傍の誘電体を無視できるという仮定は, もはや有効でなくなるのです. つまり, 変位電流が重要となり始めます. このレジームでは, 体積内の磁場を解くのではなく, 導体の表面を流れる電流をモデル化できる磁場定式化を使うべきです. 磁場インターフェースは, 導電電流と誘導電流だけでなく, 変位電流も解くことができます. 磁場 (電流のみ) インターフェースは, すべての変位電流を無視し, 導体ドメイン自体の中の導電電流と誘導電流のみを考慮します.
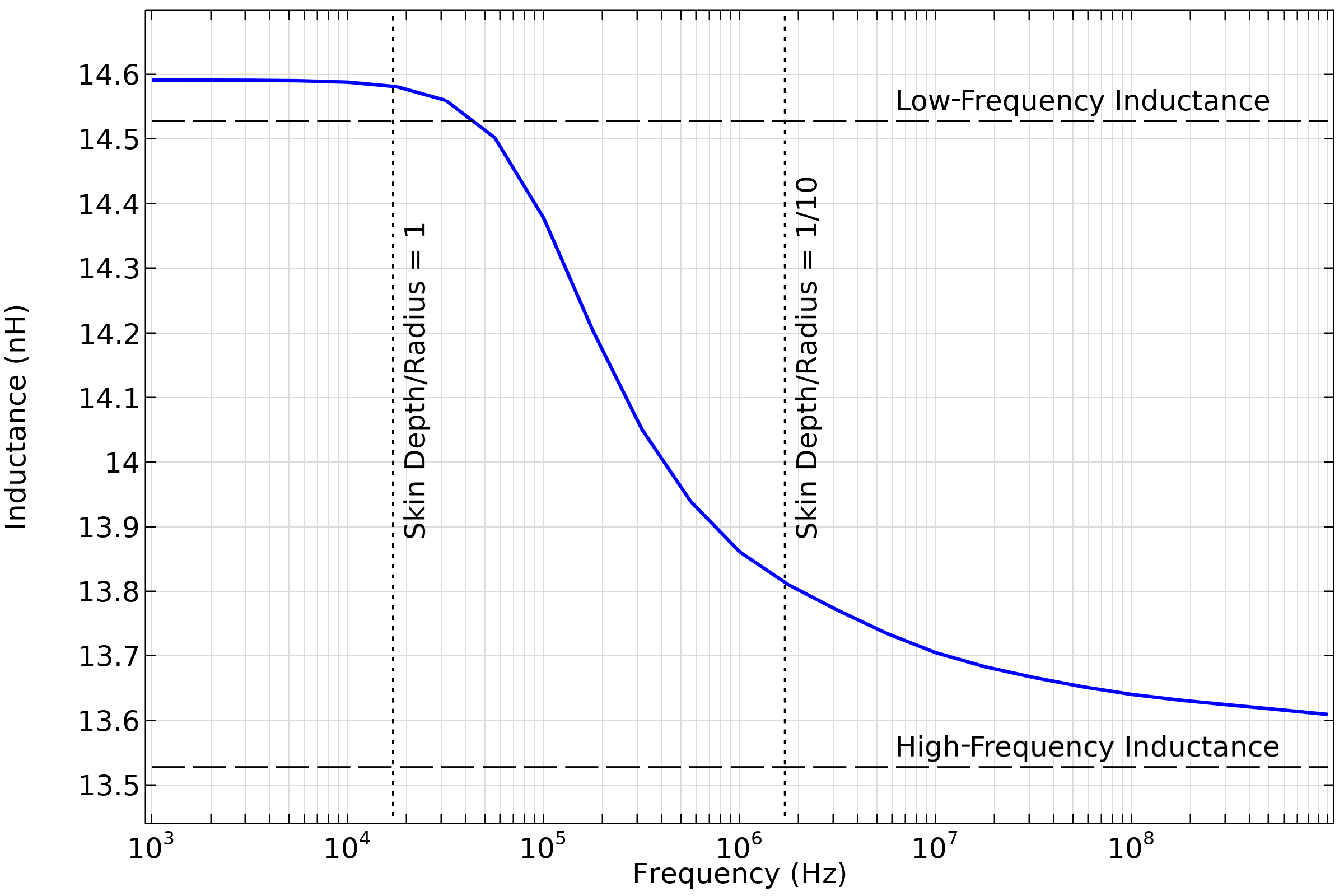
直線ワイヤーの部分自己インダクタンスを計算し, 端部効果を無視した低周波および高周波のハンドブック解と比較したもの.
さて, 部分インダクタンスの計算方法と, この定式化が適用できるレジームの範囲がわかったところで, このインターフェースを自信を持って使うにはどうすればよいでしょうか. ここで重要なのは, 測定できるのは閉ループの全インダクタンスだけで, これらの部分インダクタンスは決して測定できない, ということです. しかし, 複雑で大きな系を扱っているとすると, 全インダクタンスを計算するのはかなりコストがかかるでしょう.
小さなサブ系を1つだけ再設計することしか必要ない場合, 次の2つの仮定を立てます:
- モデル化された部品とモデル化されていない部品の間の部分的な相互インダクタンスは, 全インダクタンスに比較的小さな影響を与える.
- モデル化されていない部品の部分的な自己インダクタンスは, 比較的固定されたままである.
これらの仮定が成り立つのであれば, 系のその一部分 (あるいは数個の部分) だけをモデル化することは合理的であると言えます. 全インダクタンスを計算する必要はないかもしれませんが, 上記の仮定と, これらの部分インダクタンスが全インダクタンスに寄与するという概念を理解する限り, このサブモデルには予測的な価値があります.
では, このインターフェースの応用例として, いくつかの典型的な例を見ていきましょう.
磁場 (電流のみ) インターフェースの代表的な応用例
磁場 (電流のみ) インターフェースが役に立つ場合は, 次の通りです:
- 回路基板部品の部分インダクタンスの算出
- パワーバスシステム
- ケーブルとコネクター
- ゲート型バイポーラトランジスター (IGBT)
- 近傍磁性体のないところでのコイル
一例として, 下図のような空芯インダクターを複数個並べた回路基板があります. これまでの知識で, 単一のインダクターの部分自己インダクタンスや, 間隔の狭い複数のインダクター間の部分自己インダクタンスと部分相互インダクタンスを抽出するモデルを自信を持って構築することができるようになりました. 手始めに関連する例として, PCB コイルのインダクタンス行列計算を参照してください.

多数の空芯インダクターを搭載した電気部品. 磁場 (電流のみ) インターフェースを使用することにより, これらのインダクターのうち数個の AC 抵抗と部分インダクタンス行列を一度に計算することができます.
最後に
ここでは, 磁場 (電流のみ) インターフェースを使用して, 全インダクタンス, 部分インダクタンス, 交流抵抗を計算する方法を紹介しました. 他のアプローチに対して検証できるケースから始めることで, 全インダクタンス計算の全体的な正確さを検証しています. 次に, 部分インダクタンスと, 部分インダクタンスと全インダクタンスがどのように関連しているのかを見てみました. また, 交流抵抗の計算も見ていき, 周波数領域モデリングにおける磁場 (電流のみ) インターフェースの有効的なレジームを理解することができました. これらの情報をもとに, この種の問題に自信を持って取り組むことができるようになりました!
AC/DC モジュールについてはこちらをご覧になるか, 詳細についてはお問い合わせください.






コメント (0)