
加熱または冷却された部品が空気にさらされると, 対流によって部品から空気に熱が伝わります. 空気の動きは, ファンによって強制的に行われる場合もあれば, 空気の温度変化による自然な浮力の変化によって自由になる場合もあります. 今日は, COMSOL Multiphysics® ソフトウェアでこれらのタイプの対流をモデル化するさまざまな方法を見ていきます.
シンプルに始める: 熱伝達係数
まず, 以下に示すバスバーの電気加熱のモデルを考えてみましょう. これは COMSOL Multiphysics の入門用の例だとおわかりかもしれませんが, まだモデル化していない場合は, COMSOL Multiphysics 入門 PDF ブックレット でこのモデルを確認することをお勧めします.
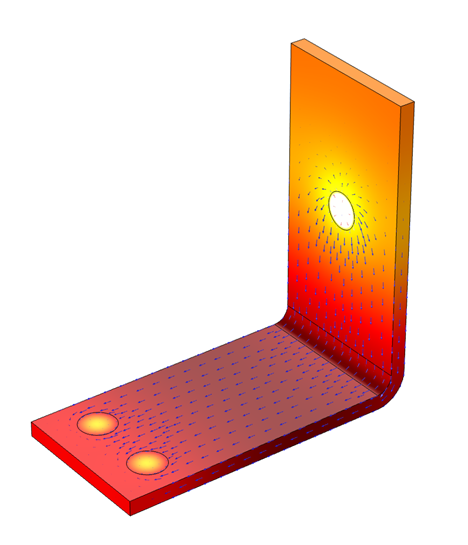
金属バスバーを流れる電流 (矢印プロット) は, 抵抗加熱を引き起こし, 温度を上昇させます (カラーサーフェスプロット).
この例では, バスバーを流れる電流をモデル化します. これにより抵抗加熱が発生し, バスバーの温度が上昇します. ボルトを介した伝導熱伝達や放射熱伝達は無視し, 周囲の空気への熱伝達のみがあると仮定します. また, この例では, 最初はバスバー上に空気を強制的に流すファンがないと仮定します. したがって, 空気への熱伝達は, 自然対流, つまり自由対流によって行われます.
部品が周囲の空気を加熱すると, 空気は熱くなります. 空気が熱くなると密度が下がり, 熱い空気は冷たい周囲の空気に対して上昇します. これらの自由対流気流により, 部品から周囲の空気への熱伝達率が上がります. 気流は温度変化と部品とその周囲の形状によって異なります. 対流は, もちろん水や変圧器油など, 他のガスや液体でも発生しますが, ここでは主に空気中の対流について取り上げます.
周囲の空気空間は, 内部 または 外部 の2つのカテゴリに分類できます. 内部とは, 部品の周囲に有限サイズの空洞 (電気接続ボックスなど) があり, その中に空気が適度に閉じ込められていることを意味しますが, 外部空間への空気の入口と出口が既知である可能性があります. この場合, 空洞の外側と入口と出口の熱境界条件は既知であると想定します. 一方, 外部とは, 物体が本質的に無限に大きい体積の空気に囲まれていることを意味します. この場合, 物体から遠く離れた空気の温度は一定の既知の値であると想定します.
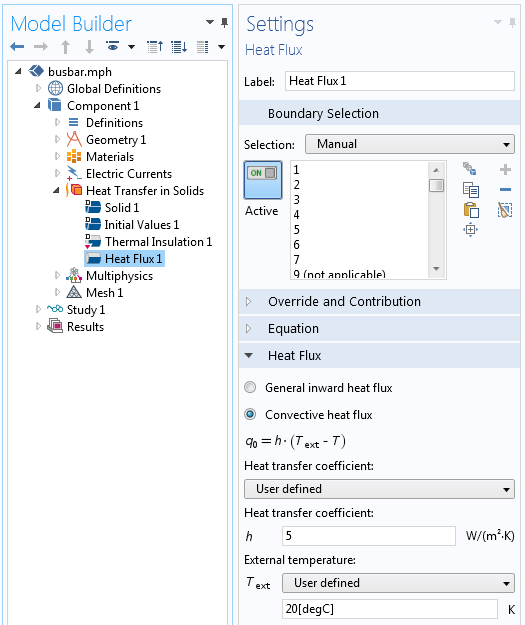
一定の熱伝達係数の設定.
入門的なバスバーの例では, 外部の空気空間への自由対流熱伝達を想定しています. これは, 熱流束の次の境界条件を使用してモデル化されます:
ここで, 外気温度は Text = 25°C で, h=5 W/m^2K は熱伝達係数です.
この単一値の熱伝達係数は, 空気の流れのすべての局所的な変動の近似値と平均を表します. この単純な系でも, h\approx 2-25 W/m^2K の間の任意の値が適切な熱伝達係数になる可能性があり, 境界ケースを試して結果を比較する価値があります.
代わりに, この構造物の上に空気を吹き付けるファンがあることがわかっている場合は, 空気の流れが速くなるため, 熱伝達係数 h\approx 10-250 W/m^2K を使用して, 熱伝達の向上を表します.
周囲の流体が水などの液体である場合, 自由および強制の熱伝達係数の範囲ははるかに広くなります. 液体の自由対流の場合, h\approx 50-1,000 W/m^2K が一般的な範囲です. 強制対流の場合, 範囲はさらに広くなり, h\approx 50-20,000 W/m^2K になります.
自由対流または強制対流の単一値の熱伝達係数を入力するのは明らかに単純化しすぎですが, なぜそうするのでしょうか. まず, 実装が簡単で, 最良のケースと最悪のケースを比較するのが簡単です. また, この境界条件は, コア COMSOL Multiphysics パッケージで適用できます. ただし, 伝熱モジュール と CFD モジュール には, より洗練されたアプローチがいくつか用意されているので, 次にそれらを見てみましょう.
対流相関の使用
対流相関 は, 一般的なジオメトリ用に開発された経験的な関係です. 伝熱モジュールまたは CFD モジュールを使用する場合, これらの相関は, 以下のスクリーンショットに示すように, 熱流束境界条件内で利用できます.
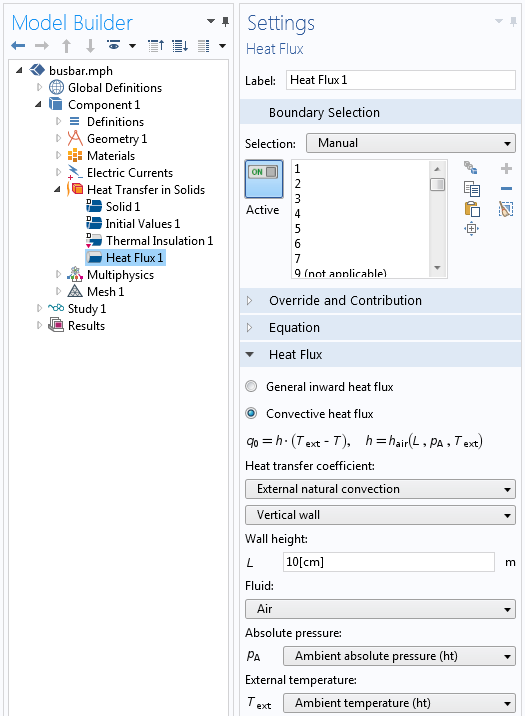
垂直壁の外部自然対流相関を含む熱流束境界条件.
これらの相関を使用するには, パーツの特性寸法を入力する必要があります. たとえば, バスバーモデルでは, 外部自然対流, 垂直壁 相関を使用し, 壁の高さを 10 cm に設定して, バスバーの垂直面らの自由対流熱流束をモデル化します. また, 外部の空気の温度と圧力も指定する必要があります. これらの値は ASHRAE データベースから読み込むことができます. このプロセスについては, 以前のブログ で説明しています.
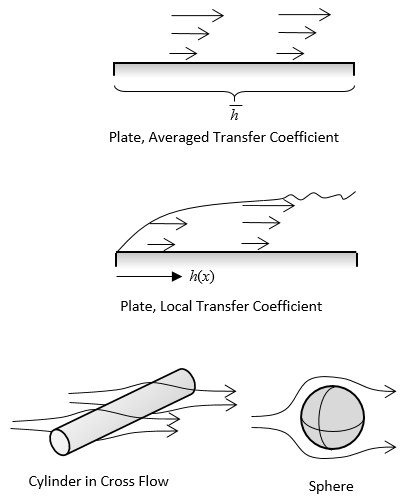
以下の表は, 利用可能なすべての相関関係の概略を示しています. これらの相関関係は, 表面形状に関する情報を取得し, ヌッセルト数相関関係 を使用して熱伝達係数を計算します. たとえば, バスバーの水平に整列した面の場合, 水平プレート, 上側 および 水平プレート, 下側 相関関係を使用します.
強制対流相関関係を使用する場合は, 空気の速度も入力する必要があります. これらの対流相関関係は, 十分に確立された実験データに基づいているため, 現実をより正確に表現できるという利点があります. これらの相関関係は非線形境界条件につながりますが, 通常は一定の熱伝達係数を使用する場合よりも計算時間がわずかに長くなるだけです. 欠点は, 部品の形状に適した経験的関係がある場合にのみ使用が適切であることです.
| 自由対流 | 強制対流 | |
|---|---|---|
| 外部 | 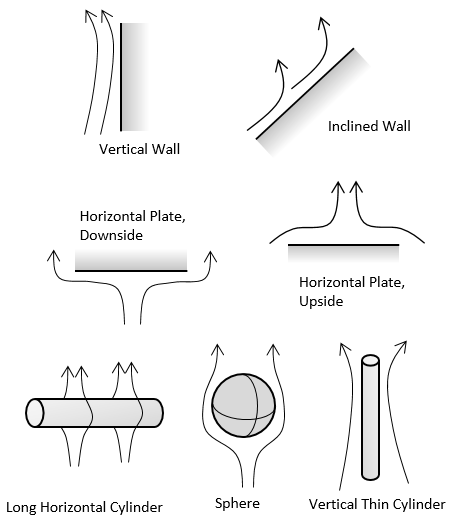 |
 |
| 内部 | 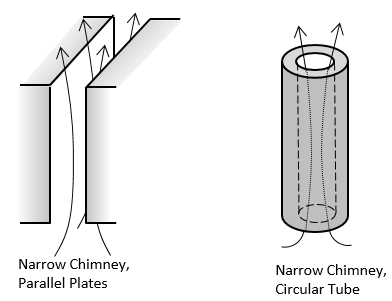 |
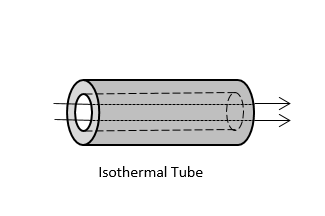 |
利用可能な 対流相関 の境界条件.
上記の対流相関はすべて, 内部として分類されているものも含め, 流体の無限の外部リザーバー (周囲の空気空間など) の存在を前提としていることに注意してください. 表面から運び去られた熱は, 温度を変えることなくこの周囲の空気空間に入り, 入ってくる周囲の空気は既知の温度です. ただし, 完全に密閉された容器内の対流を扱っている場合は, これらの相関のいずれも適切ではなく, 別のモデリング手法に移行する必要があります.
強化された熱伝導率を使用した筐体内の自由対流の近似
長方形の空気で満たされた空洞を考えてみましょう. この空洞の垂直面の1つが加熱され, もう1つが冷却されると, 空気が規則的に循環します. 同様に, キャビティが下から加熱され, 上から冷却される場合, 空気の循環が発生します. これらのケースは, 温度分布と空気の流れの両方を解析して生成された以下の画像に示されています.
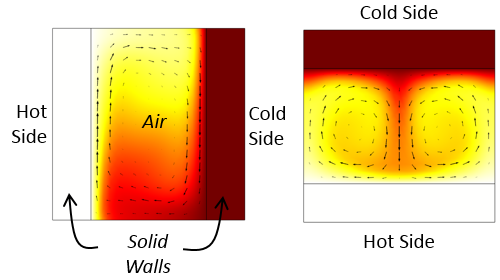
垂直および水平に整列した長方形キャビティ内の自由対流.
自由対流を解くのはかなり複雑です. たとえば, 自然対流のモデリング に関するこのブログを参照してください. したがって, より単純な代替案を見つけたいと思うかもしれません. 伝熱モジュールには, 対流の等価伝導率 機能を使用するオプションがあります. この機能を使用すると, 下のスクリーンショットに示すように, 水平および垂直の長方形キャビティの場合の相関関係に基づいて, 空気の有効熱伝導率が増加します.
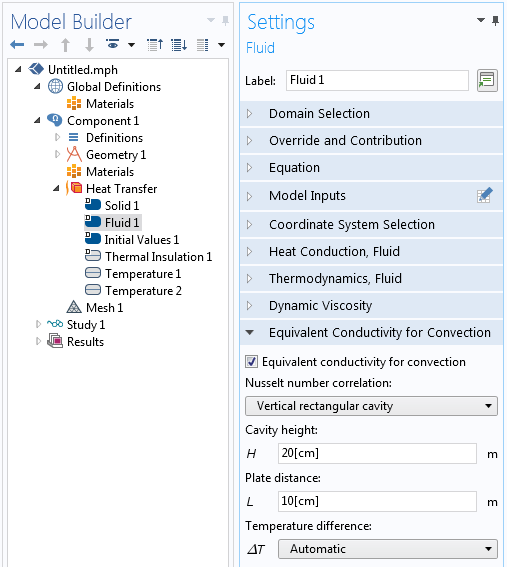
対流の等価伝導率機能と設定.
空気領域は, 伝熱 インターフェース内の 流体 領域機能を使用して明示的にモデル化されていますが, 空気の流れ場は計算されず, 速度項は単に無視されます. 熱伝導率は, キャビティの寸法とキャビティ全体の温度変化に依存する経験的相関係数によって増加します. キャビティの寸法を入力する必要がありますが, ソフトウェアはキャビティ全体の温度差を自動的に判断して更新できます.
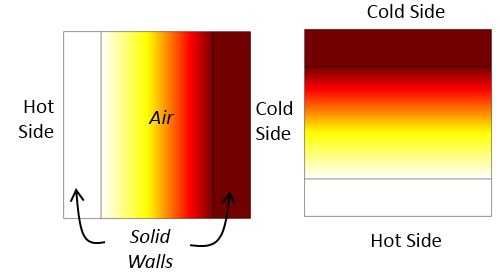
対流の等価伝導率機能を使用した, 垂直および水平に整列したキャビティ内の温度分布. 自由対流の空気流は計算されません. 代わりに, 空気の熱伝導率が増加します.
完全に閉じたキャビティ内の自由対流を近似するこのアプローチでは, 空気領域をメッシュ化し, 空気の温度場を解く必要がありますが, 通常は計算コストがわずかに増加するだけです. このアプローチの欠点は, 長方形以外の形状にはあまり適用できないことです.
等温領域を使用した筐体内の強制対流の近似
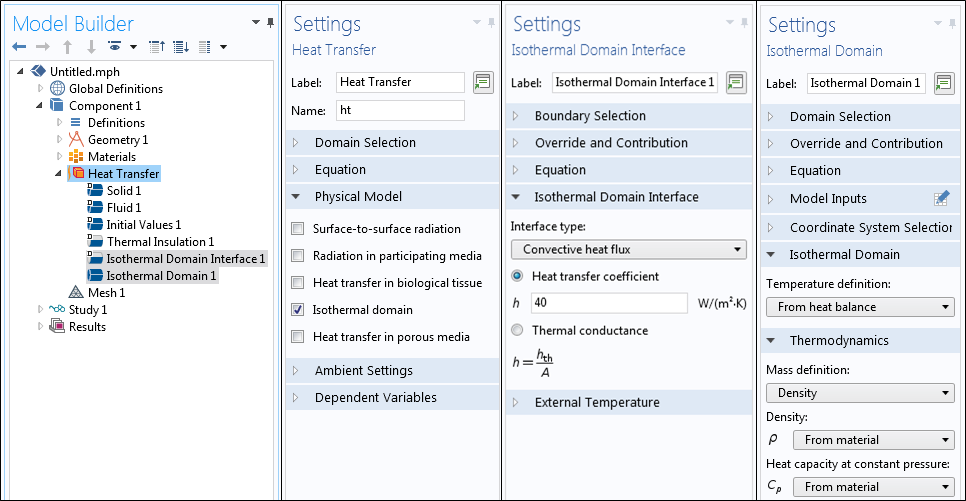
次に, 完全に密閉された筐体を考えてみましょう. ただし, 内部に空気を積極的に混合するファンまたはブロワーがあります. 十分に混合された空気は, キャビティ全体で一定温度であると想定できます. この場合, 設定ウィンドウで 等温領域 オプションを選択すると, 伝熱モジュールで使用できる 等温領域 機能を使用するのが適切です.
等温ドメイン機能を使用して, 十分に混合された空気ドメインを明示的にモデル化できます. モデルでは, ドメイン全体の温度は一定値です. 空気の温度は, 境界を介してドメインに出入りする熱のバランスに基づいて計算されます. 等温ドメイン境界は, 次のいずれかのオプションに設定できます.
- 断熱: 境界を越える熱伝達なし
- 連続性: 境界を越える温度の連続性
- 換気: 等温ドメインに出入りする既知の温度の流体の既知の質量流量
- 対流熱流束: 前述のように, ユーザーが指定した熱伝達係数
- 熱接触: 特定の熱抵抗
これらの境界条件オプションのうち, 密閉されたキャビティ内のよく混合された空気には, 対流熱流束 が最も適しています.
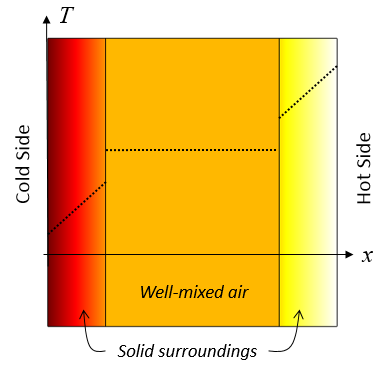
等温領域機能を使用した場合の代表的な結果. 十分に混合された空気領域は一定温度であり, 指定された熱伝達係数を介して周囲の固体領域に熱が伝達されます.
空気の流れを明示的にモデル化する
最も計算コストがかかるアプローチですが, 最も一般的なアプローチでもありますが, 空気の流れを明示的にモデル化することです. 強制対流と自由対流の両方をモデル化できるほか, 内部または外部の流れをシミュレートできます. このタイプのモデル化は, 伝熱モジュールまたは CFD モジュールのいずれかを使用して実行できます.
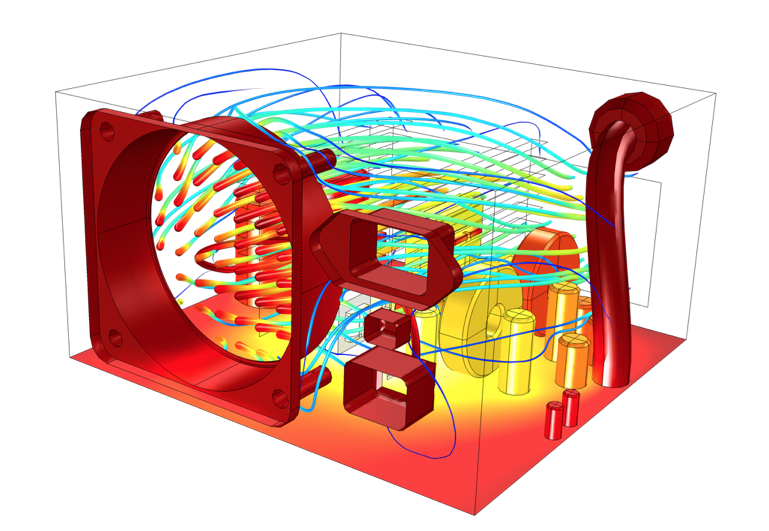
筐体内の空気の流れと温度の計算 の例.
COMSOL Multiphysics 入門 ブックレットを終えた場合は, すでに内部強制対流モデルの例を1つ求解しています. 空気の流れを明示的にモデル化する方法については, この投稿の最後に記載したリソースで詳しく学ぶことができます.
自由対流を完全に無視できるか?
このトピックの最後に, 空気中の自由対流を無視できるのはいつで, このようなケースをどのようにモデル化できるのかという疑問に答えます. 部品間の隙間が狭い場合や非常に細いチューブなど, キャビティの寸法が非常に小さい場合, 粘性減衰が浮力を上回る可能性があります. この粘性力と浮力のバランスは, 無次元レイリー数 によって特徴付けられます. 自由対流の開始は, 境界条件と形状によって大きく異なります. 経験則としては, 1 mm 未満の寸法では自由対流は発生しない可能性が高いですが, 空洞の寸法が 1 cm を超えると自由対流が発生する可能性が高くなります.
では, これらの小さな隙間を通る熱伝達をどのようにモデル化できるでしょうか. 空気の流れがない場合, これらの空気で満たされた領域は, 対流項のない固体または流体として単純にモデル化できます. これは, 窓とガラスの熱性能 チュートリアルで実証されています. また, マイクロスケールの密閉構造内の空気を固体としてモデル化することも適切です.
これらの薄い隙間が, 解析対象の系の他の寸法に比べて非常に小さい場合は, 薄層境界条件を使用して 熱的に厚い近似 レイヤータイプでモデル化することで, 隙間をさらに簡略化できます. この境界条件は, 指定された厚さと熱伝導率に基づいて, 内部境界全体で温度の急上昇をもたらします.
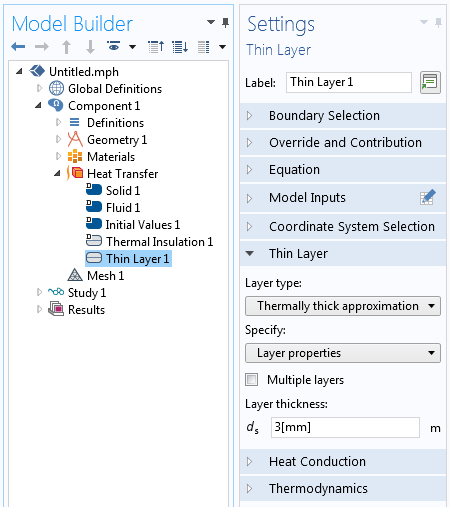
薄層境界条件は, 部品間の薄い空気の隙間をモデル化できます.
コア COMSOL Multiphysics パッケージ内では, 前の2つのアプローチを使用できます. 伝熱モジュールには, 薄層条件の追加オプションがあり, 複数の材料層で構成できる, より一般的な多層境界を考慮することができます.
COMSOL Multiphysics® での自然対流と強制対流のモデル化に関する締めくくり
この議論を締めくくる前に, 輻射熱伝達の問題にも簡単に触れておく必要があります. ここでは輻射については説明していませんが, エンジニアは常に輻射を考慮する必要があります. 周囲条件にさらされた表面は周囲に熱を輻射し, 太陽によって加熱されます. 太陽からの輻射加熱の規模は大きく, 1 平方メートルあたり約 1000 ワットであり, 無視できません. 周囲条件への輻射熱伝達のモデル化の詳細については, この 以前のブログ をお読みください.
内部表面間でも 輻射熱伝達 が起こります. 表面間の輻射熱流束は, 温度差の4乗の関数です. 20°C と 50°C の 2 つの表面間の輻射熱伝達は最大で 1 平方メートルあたり 200 ワットですが, 20°C と 125°C の表面では 1 平方メートルあたり 1000 ワットに上昇することに注意してください. 表面間の輻射熱伝達を正しく計算するには, 熱伝達モジュールを使用して 形態係数を計算する ことも重要です.
今日は, 対流をモデル化するいくつかのアプローチを見てきました. 最も単純なアプローチである一定の対流熱伝達係数を使用するアプローチから始めました. 次に, 経験的対流相関境界条件の使用について説明し, その後, ドメイン内の有効熱伝導率と等温ドメイン機能を使用する方法について説明しました. これらのアプローチは, 精度が高く, 計算コストがわずかに高いだけです. 最も計算量の多いアプローチ (流れ場を明示的に計算する) は, もちろん最も一般的なものです. また, 自由対流を完全に無視することが適切な場合と, そのような状況をモデル化する方法についても触れました. これで, 自由対流と強制対流をモデル化するための利用可能なオプションとトレードオフについて理解が深まったはずです. モデリングを楽しんでください!
追加資料
- COMSOL ブログで空気の流れと熱伝達を明示的にモデル化する方法を学びましょう
- アーカイブウェビナー で熱伝達のシミュレーションの概要をご覧ください






コメント (0)