
代数マルチグリッド (AMG) ソルバーは, 大規模な CFD シミュレーションに堅牢なソリューションを提供します. COMSOL Multiphysics® ソフトウェアのバージョン 5.3a 以降で利用可能な AMG 法では, 少なくとも1つの粗いメッシュを必要とするジオメトリマルチグリッド (GMG) ソルバーとは対照的に, 1つのメッシュのみが必要です. これにより, 細かいメッシュを使用しない限りメッシュ化が難しい細かいディテールを持つ複雑なジオメトリに対して粗いメッシュを作成する手間が省けます.
流体の流れの問題, 数学モデル, 数値モデル
流体の流れは, 運動量, 質量, エネルギーの保存則によって正確に記述できます. これらの法則を記述する最も正確な方法は, 偏微分方程式 (PDE) を使用することです. これらの法則を記述する PDE 系は非線形です. ほとんどの実際のケースでは, これらの方程式を解析的に解くことはできません. 代わりに, 空間と時間で離散化して, 解ける代数方程式の形で PDE の近似値を得ることができます. 数学モデルを数値モデルで近似すると言えます.
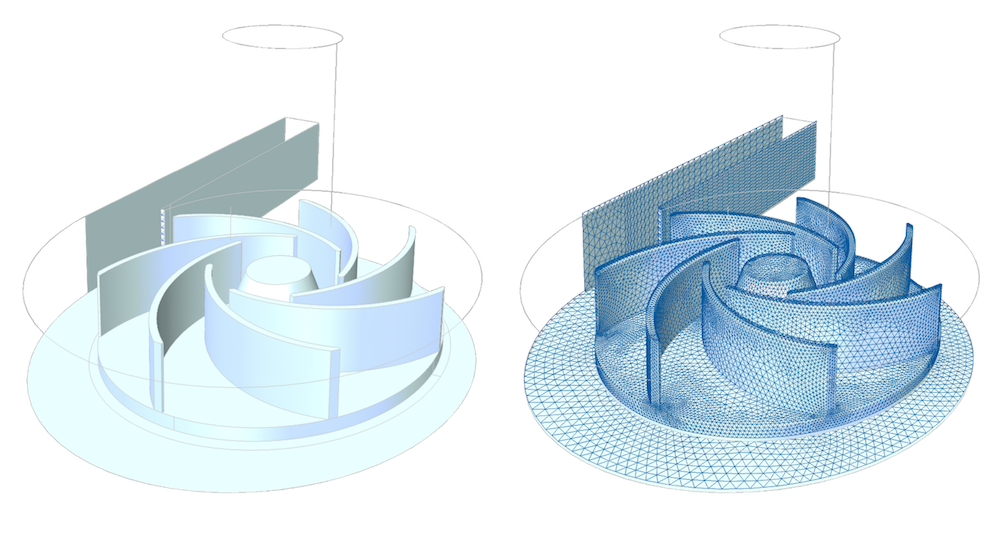
左側のジオメトリの “実際の” 記述は, 各要素の運動量バランスと質量バランスが実行される離散化記述で近似されます.
空間と時間の問題の場合, COMSOL Multiphysics は線の方法を使用します. 空間の離散化は有限要素法を使用して行われ, 時間の離散化は, 後方微分公式 (BDF) や一般化 α などの常微分方程式の標準的な方法を使用して行われます.
流体の流れ方程式は非線形であるため, 離散化された数値モデル方程式も非線形です. 過渡的な問題の場合, 非線形方程式の系をすべての時間ステップで解く必要があります. 定常流の場合, 数値モデル方程式は, 一度解く必要がある非線形方程式の系を形成します.
時間依存問題と定常問題の両方において, 非線形方程式の系を解く方法は, 系が完全に結合して解かれる場合, 減衰ニュートン法です. この方法は, 非線形方程式の線形化と, ニュートン反復と呼ばれる一連の反復で線形方程式を解くことに基づいており, 必要な精度が得られます.
線形方程式系に反復法を使用する必要があるのはなぜか
私たちの場合, 方程式と未知数は数十万から数百万に上り, 数値方程式を生成するために使用した有限要素メッシュのノード数に比例します. 各ニュートン反復で解く必要がある線形方程式系は, 直接ソルバーで解くにはコストがかかりすぎます. ただし, 反復ソルバーを使用すると, はるかに少ないメモリで線形方程式を解くことができます.

遠心ポンプ内の流れのこの比較的単純なモデルでも, 350,000 の方程式と未知数が必要です. AMG ソルバーのおかげで, デスクトップコンピューターで方程式を解くことができます.
流体の流れの問題の場合, COMSOL Multiphysics は一般化最小残差 (GMRES) 法を使用します. これは, 非常に大規模な線形方程式系を解くための反復法です. 線形方程式系を変更することで, GMRES 法のパフォーマンスを大幅に向上させることができます.
マルチグリッド法
マルチグリッド法は, GMRES 法などの反復手法の方程式系を変更または事前調整するための最適な技術を提供します.
GMG 法は, 細かいメッシュから粗いメッシュまで, さまざまなメッシュレベルの線形方程式系に作用します. 解の候補, つまり反復を, より粗いメッシュとより細かいメッシュに対応する異なる線形系間で転送します. その考え方は, 直接法は最も粗いメッシュに対してのみ解かれ, この情報を使用してより細かいメッシュレベルの解をより迅速に見つけるというものです. ただし, 粗いメッシュの場合でも, 求解パフォーマンスに影響を与えない程度には小さくする必要があります.
GMRES の各反復では, GMG 法はより細かいメッシュから進み, 系の右側の辺を取得し, より細かいレベルの近似解を プレスムージング と呼ばれるプロセスで粗いメッシュにマッピングします. 方程式の解は, 直接ソルバーを使用して最も粗いレベルで修正されます. 次に, この解は ポストスムージング と呼ばれるプロセスで再び細かいレベルにマッピングされます.
メッシュレベルを上下するプロセス (V サイクル) は, GMRES の各反復で繰り返すことができます. GMRES 反復の許容値に達すると, 線形系に対する十分な解が得られます.
AMG 法を使用する理由
GMG 法は, 流体の流れの問題に非常に効果的です. ただし, 非常に重大な制限があります. 複雑な形状の場合, 最も粗いレベルで解くのに十分なほど小さい方程式系を提供する粗いメッシュを生成することは困難またはほぼ不可能です.

遠心ポンプの薄いブレードにより, ブレードの周りの流体の要素が非常に小さくなります. これはまた, 最も粗いメッシュレベルでも, GMG を使用した直接ソルバーで求解するには要素が多すぎるため, 方程式が多すぎることも意味します.
AMG 法では, 異なるメッシュレベルは必要ありません. AMG 法の粗化プロセスは, 線形方程式系の構造のみ, より正確には方程式系の左辺を表す行列に基づいています. この方法では, より少ないエントリに接続されている行列内のエントリを, より小さなサイズの新しい行列に集約します. エントリを集約するプロセスは繰り返すことができ, さらに小さな行列を構築できます. 次に, 実行された集約の数に応じて, これらに異なるレベルが割り当てられます. プレスムージング, ポストスムージング, および最も粗いレベルの解決を含むマルチグリッドサイクルの原理は, さまざまなレベルで構築された行列の GMG 法の場合と同じです.
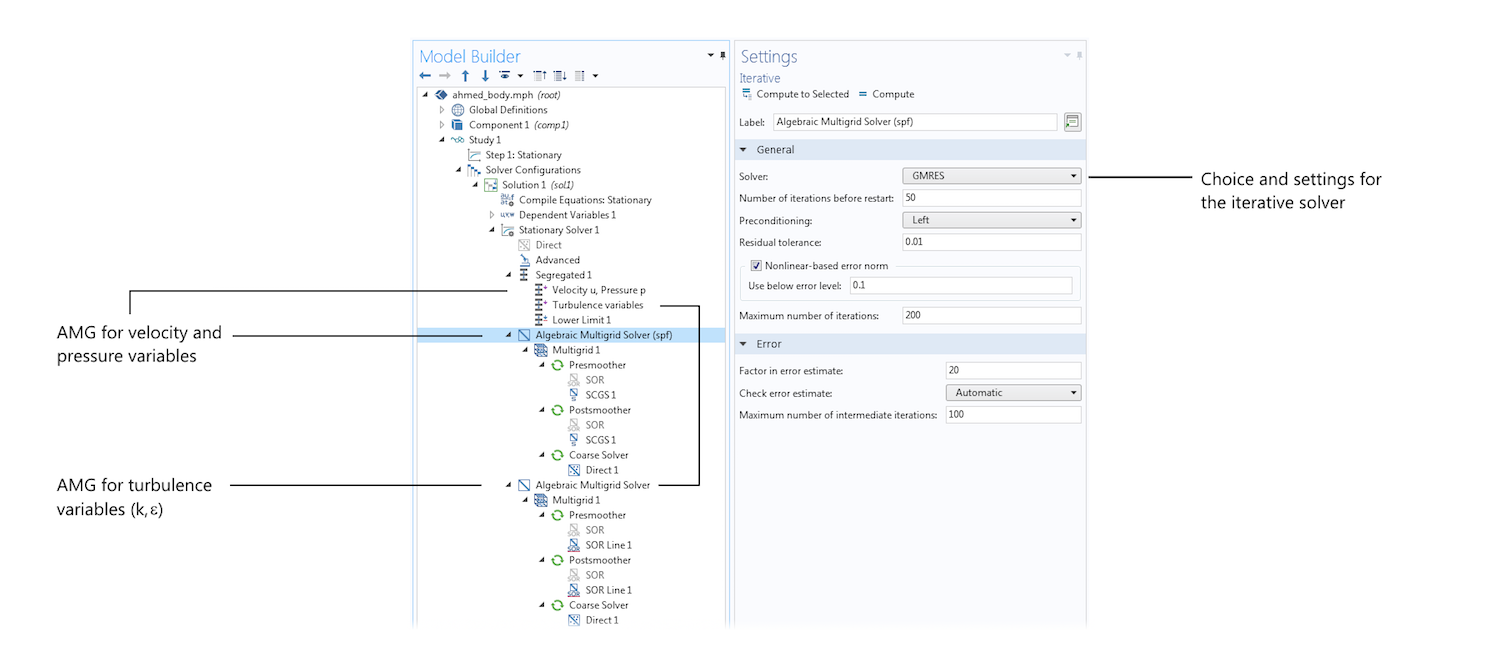
以下に示す Ahmed ボディのモデル方程式を解くために AMG 法と組み合わせて使用される反復ソルバー (GMRES) の設定. この方法は, 分離型ソルバーで2つの別々のステップで運動量および連続方程式 (u, v, w, p) と乱流モデル変数 (k, ε) を解くために使用されることに注意してください.
パフォーマンス
COMSOL Multiphysics のさまざまなソルバー設定のパフォーマンスを監視するために, 毎日数千のテストが実行されます. 反復ソルバーと流体流れのテストケースの1つは, いわゆる Ahmed ボディモデルです. もう1つのテストは, いわゆるラミナースタティックミキサーテストです. 測定結果によると, 630万自由度の場合, AMG 法はシングルコアコンピューターで約 13% 短い解析時間で GMG 法よりも優れています.
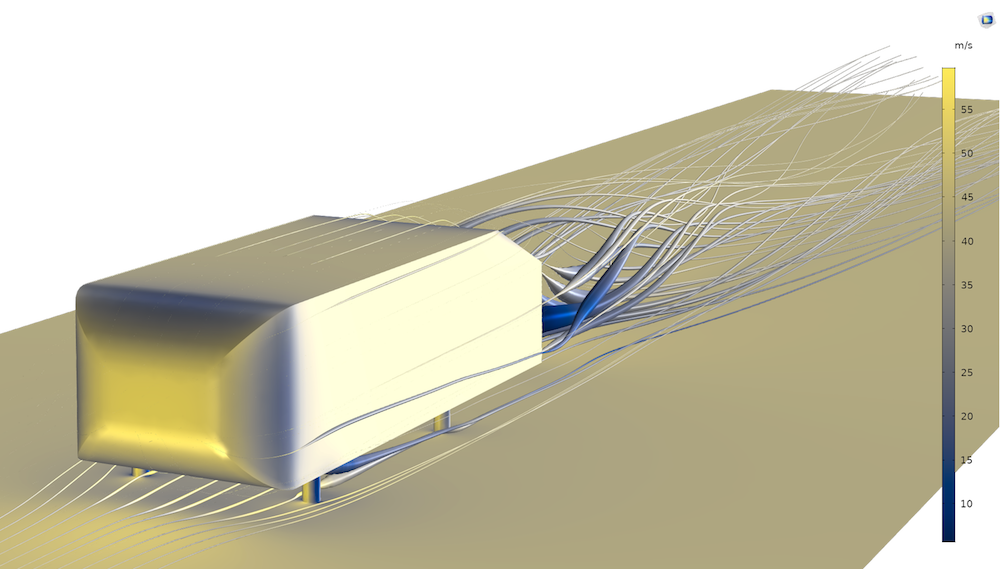
Ahmed ボディは乱流のベンチマークモデルであり, 一般的な乱流モデルの検証モデルです.
これらの結果は, これらの方法の COMSOL Multiphysics 実装を反映したものであり, この方法の一般的な特性を反映したものではないことに注意してください. 4コアのコンピューターでは, この差は約 6% に低下します. 32コアの場合, 2つの方法は同等です. この動作の理由は, GMG ソルバーが AMG ソルバーよりも高いレベルで並列化されているためです. 新しい AMG 法は, 最初の1年間ですでに優れた堅牢性と優れたパフォーマンスを示しており, GMG メソッドのベストケースシナリオと同等です.
次のステップ
下のボタンから, 数値モデリングのニーズに対応する COMSOL Multiphysics の主な機能について詳しく学んでください.
COMSOL ブログでマルチグリッド法の使用について詳しく読む:






コメント (0)