なぜゴルフボールにはディンプルがあるのか？

ディンプルは, ゴルフボールの空力特性にとって非常に重要であることはよく知られています. ディンプルが乱流を発生させ, ボールの抗力を減少させるのです. しかし, これは直観に反しているように聞こえませんか? 一般的に, 滑らかな物体は粗い物体よりも空気力学的に優れていると言われています. 今日のブログでは, この一見パラドックスの詳細を調べ, この知識を使って COMSOL Multiphysics® ソフトウェアでゴルフボールの軌道をモデル化し最終的にボールを打つのに最適な角度を見つける方法を学びます. ホールインワンも夢ではありません.

観察から数理モデルへ

子供の頃, ゴルファーがいない雨の日に, 家族と一緒に近くのゴルフ場を歩くことがありました. 私たち独自のゲームとして, 前の不運なゴルファーが落としたボールを探すという遊びをしていました. 最も多くのボールを見つけた人が勝者となる, といったルールでした. 雨の日が続くと, 私たちのゴルフボールのコレクションはどんどん増えていったのですが, 私たちの誰もゴルフの遊び方を知らなかったにも関わらず, ボールのくぼみの形には理由があると思っていました. おそらく美観のためか, ボールをより速く空中に飛ばすためといったところでしょうか.

ゴルフボールにディンプルがあるのはなぜか, 考えたことはありますか?

年が経ち, 今では私はゴルフコースでゴルフボールを失う不運なゴルファーとなってしまいました(人生は一周したと言えるでしょう). しかし, 私は今, エンジニアの観点から, あの見慣れた球体をもう一度見てみることができます. なぜディンプルがあるのか? COMSOL Multiphysics でゴルフボールをモデル化することはできるのか? ボールの紛失を減らしてパーを取るために, ショットを最適化することはできるのか? 以前のブログのおかげで, ゴルフスイングは上達しましたが, もっと情報が必要だったので, 教科書に戻ってみました.

抗力危機の観察

歴史上, さまざまな形の周りの流れが科学者によって研究されてきました. たとえば, 円柱の周りの流れは, 渦列を発生させます. 球体の場合は, このような大きな流れの交互構造は発生しませんが, 流れの特性はレイノルズ数と関連していると考えられます. d密度\rho, 動粘度\mu, 速度Uの流体中の直径(変数)の球の場合, 次のように定義されます.

(1)

レイノルズ数の値が低い場合, 流れは層流であると言われ, 粘性力が支配的です. 一方, レイノルズ数が大きい場合, 流れは乱流になり, 慣性力が支配的になります. 抗力Dの絶対値, つまり流れに対するオブジェクトの抵抗を比較する代わりに, 無次元抗力係数C_Dを次のように定義するのが一般的な方法です.

(2)

ここで, A= \dfrac{1}{4} \pi d^2はボールの断面積です.

流動様式に応じて, 球の抗力係数が一定ではなく, 短いレイノルズ数の範囲で劇的に変化することが, Gustave EiffelとLudwig Prandtlによってほぼ同時に観測されました. このような抗力係数の急激な低下は抗力危機と呼ばれ, サッカーボールやフットボールボールなどの他の種類のボールでも見られます. 唯一の違いは, 次の画像で見られるように, その場所です.

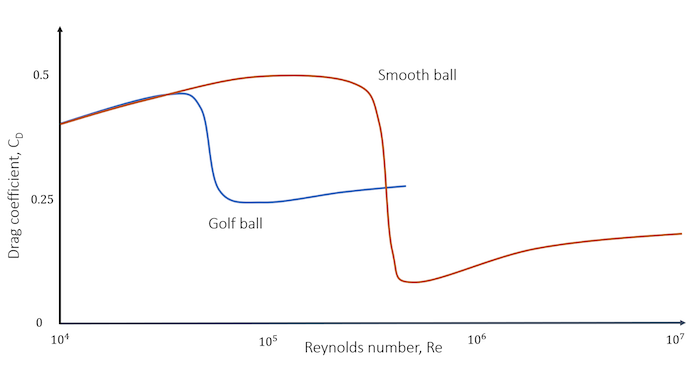
滑らかなボールとゴルフボールの抗力係数分布の比較. ディンプルによって抗力危機がレイノルズの低い値にシフトしていますが, 滑らかなボールと比較してこの低下はそれほど重要ではありません. また, ゴルフボールの抗力係数は, 限られたレイノルズ値の範囲でのみ小さくなっていることにもご注目ください.

ドライバーが打つゴルフボールの典型的な速度が時速260km程度であることと, ゴルフボールの公式デザイン (d= 42.67 mm)を考慮すると, 典型的なレイノルズ数は2\cdot10^5となります. 前述のグラフから推測されるように, これにより抗力係数はレイノルズ数の最適な範囲に収まり, 滑らかなボールの約半分の値になります. ゴルフボールにディンプルがあるのはこのためです. ゴルフボールが到達する特定のレイノルズ数の範囲では, 抗力が小さくなるため, ボールはより遠くまで飛ぶことができるのです.

この答えでは満足してもらえないかもしれません. ディンプルのあるゴルフボールは抗力が小さいことはご解説しましたが, 低速で抗力危機が起こる理由はまだご説明していません. この現象を理解するためには, 球体の周りの流れを詳しく見てみる必要があります.

空気抵抗危機の理由

まず最初に, 物体の抗力は2つの原因で発生することを思い出していただけると思います.

1. 圧力抗力(フォーム抗力とも呼ばれる), ボディ周囲の圧力分布によって発生する
2. 境界線に沿って生じるせん断応力による粘性抵抗

滑らかな球のような鈍重な物体では, 圧力抗力は計算されたレイノルズ数の範囲で最も大きくなります. その結果, 球体の周りの圧力分布がその全体の抗力を決定することになります.

乱流の理論についてはあまり触れずにご説明すると, まず球体の前面に層状境界層が形成されます (流れは質量や運動量をほとんど交換しない異なる層に分離されます). この時点から, 流れの種類に応じて2つの選択肢があります.

1. 流れが十分に層流であれば(レイノルズ数が低い), 境界層が乱流境界層に移行する間もなく, 約82度に等しい角度の逆向きの圧力勾配によって分離し, 球体の後ろに大きな伴流ができます.
2. 流れが十分に乱れていれば, 臨界82度に到達する前に, 境界が乱流に移行する時間があります. このとき, 流れの混合状態が良くなり, 境界層の上部からの運動量の交換が可能になります. これにより, 境界層の下部が活性化され, 壁付近の速度勾配が大きくなり, 流れの分離が120度前後の角度まで遅れるのです. 流れが表面によく「くっついて」いるように見えます.

ゴルフボールと滑らかな球の伴流の比較. レイノルズ数は約1e5です.

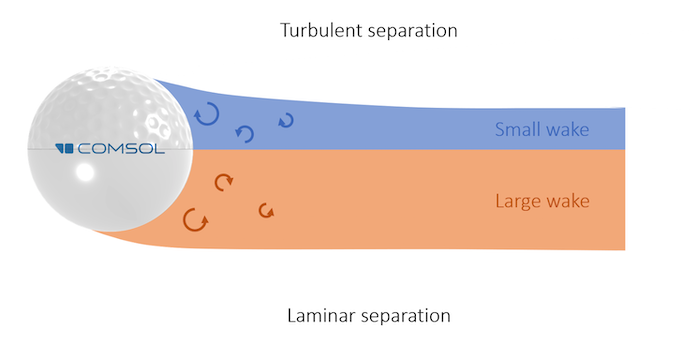
乱流境界層の分離により発生したディンプル付きゴルフボール(上)と層流境界層の分離により発生したスムースボール(下)の伴流を比較したもの. ディンプルボールの分離点は下流側にあり, 伴流が小さいことにご注目ください.

乱流の伴流では多くのエネルギーが失われ, 圧力が大きく低下します. したがって, 支配的な抗力である球体の圧力抗力は, 主に伴流域の大きさに影響されます. これらの情報を踏まえると, 抗力係数のグラフをより理解していただきやすいはずです. ゴルフボールの場合は,

• 層流境界層から乱流境界層への移行は, ディンプルによって引き起こされる小さな渦によって, レイノルズ数が低いほど起こります. これにより伴流が小さくなり, 抵抗が小さくなります.
• 滑らかなボールに比べて, 抗力危機はそれほど深くありません. 同じような伴流の大きさであれば, 表面が荒れていることで, 前部からの粘性抵抗が無視できなくなります.

ゴルフボールの空力のモデル化

これで, そもそも, ゴルフボールにディンプルがある理由がわかりました. 抗力が小さくなることで, ボールがより遠くまで進むことができることを覚えておきましょう. ボールが実際にどれくらい遠くまで行けるかを調べるには, まずボールの軌道を計算する必要があります. ボールに作用する力と初期条件を次の図に示します. ただし, ボールは対応する体積の空気よりも1000倍近く重いので, 浮力の影響は無視します.

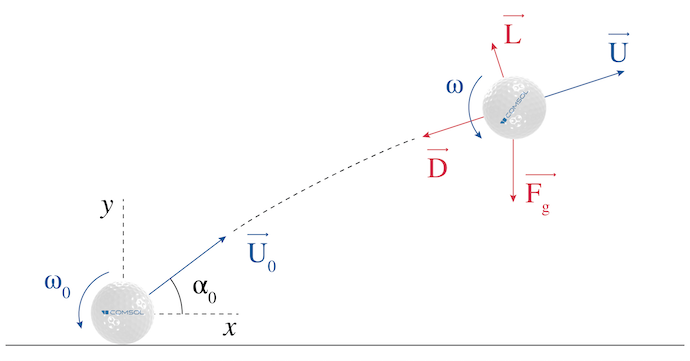
初期条件とゴルフボールのショットに作用する力.

初期状態は, 前回の性能解析の最終結果から, シャフト速度145km/h(90mph)の7番アイアンでボールを打った場合を想定しています.

• ボール初速: 187km/h(116mph)
• 初期のスピンレート: 6113 rpm
• 初期打上げ角度: 17.4°

質量mのボールにニュートンの第2法則を用いて, 加速度\overrightarrow{a}と重力\overrightarrow{F_g}を記録します.

(3)

抗力Dのノルムは, 式(2)を並べ替えることで求められます.

(4)

同様に, マグナス効果による揚力Lは, ボールのスピンレート\omegaに依存する揚力係数C_Lで定義されます.

(5)

ゴルフボールのスピンレートにおける揚力係数の依存性は, 1976年にBearman氏とHarvey氏によって広範囲に研究されました(参考文献1). 彼らはまた, 抗力係数も回転に依存するはずであることを観察しました(第1図の曲線は, ある特定のスピンレートに対して有効です). より一般的な記述のために, 周辺速度と流速の比である無次元のスピンファクターSが導入されています.

(6)

この結果は古いゴルフボールで得られたものであり, 現在では曲線が異なる可能性があると言えるかもしれませんが, Bearman氏とHarvey氏の結果は, 利用可能な文献の中で最大の範囲のレイノルズ数とスピンファクターをカバーしています. したがって, このブログで得られた結果は, 現代のゴルフボールの真の値として受け取られるべきではありません. 次の曲線は, カーブデジタイザーアプリを使用して参考文献1の図9から取得したデータに, COMSOL モデルとカーブフィッティングアプリの併用を用いて3次多項式カーブをフィッティングすることによって得られました.

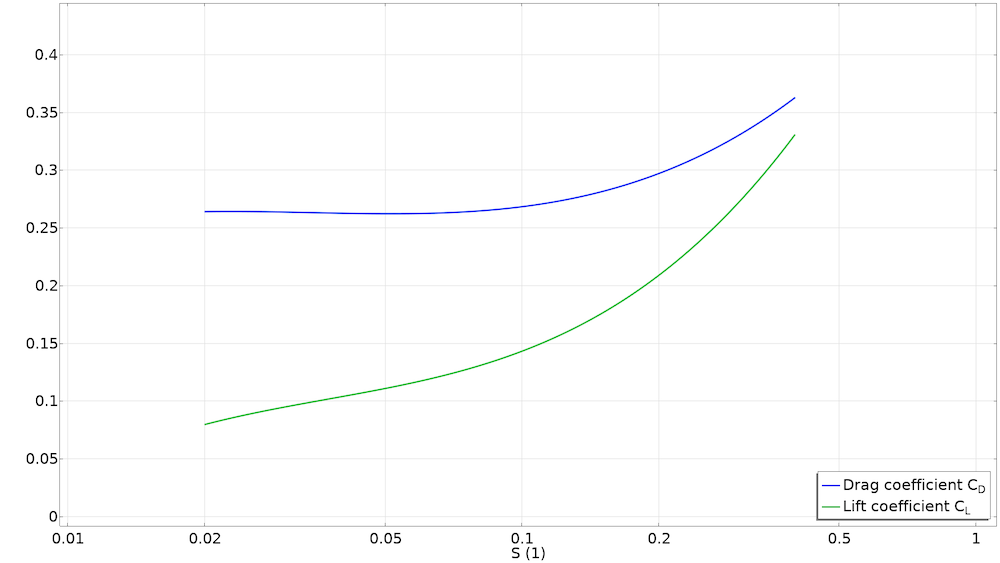
スピン係数に対する抗力係数と揚力係数の分布.

滑らかなボールの抗力係数は, 標準の抗力相関 (最初の画像を参照)から引用され, 揚力係数は回転するゴルフボールの揚力係数と等しいと概算されます(実際には, この係数はもっと小さくなります).

最後に, 摩擦によって回転が遅くなるので, SmitsとSmithによって提案された指数関数的な減衰を用いてスピンレートをモデル化することができます(参考文献2).

(7)

ここで, c=10^{-4}は実験定数です.

抗力はボールの動きと逆になり, 揚力は垂直になると考えると, x– 軸とy-軸に投影して次の式が得られます.

(8)

ここで, U=\sqrt{\dot{x}^2+\dot{y}^2}です.

この方程式系は常微分方程式(ODE)で構成されており, すべての変数の間に依存関係があるため複雑に見えるかもしれません. しかし, 実際には COMSOL Multiphysics® を使って簡単に実装し, 求解することができます.

COMSOL Multiphysics® でのゴルフボールモデルの実装ボールの位置を解く大域方程式の系

この問題を実装する最も簡単な方法は, 0Dコンポーネントでイベントインターフェースを使用することです. このコンポーネントでは, グローバル方程式ノードを使用して式8のシステムを解き, ボールが地面に触れたときに計算を停止することができます. (y=0)

スタディで使用する変数の設定.

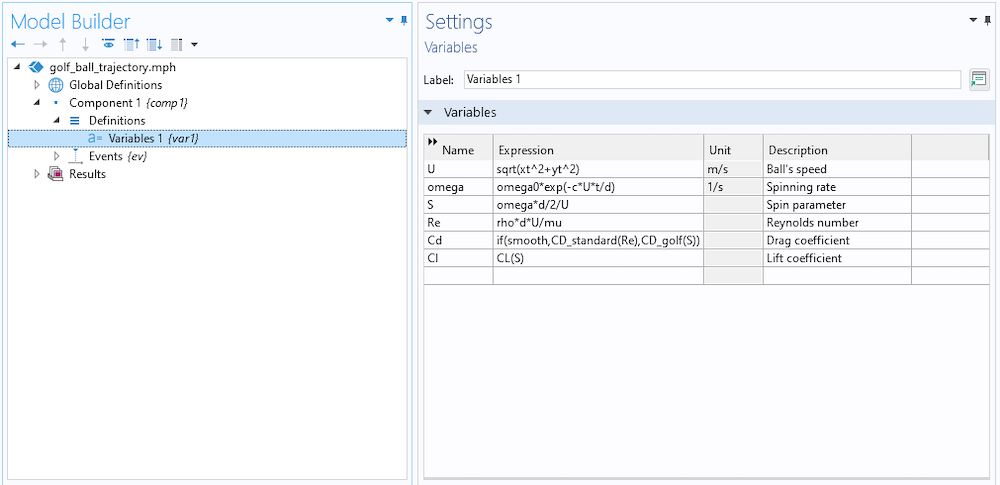
最初のステップは, 本スタディで使用されるさまざまな変数を設定することです. ここでは，さまざまな関数やグローバルパラメーターを使って計算されます. 特に，パラメーターsmoothは，打ち出されるボールの種類を決定します.

• ディンプルゴルフボール(smooth=0)
• 滑らかなボール(smooth=1)

量xtと ytは, イベントインターフェースによって計算された, 位置の時間微分です.

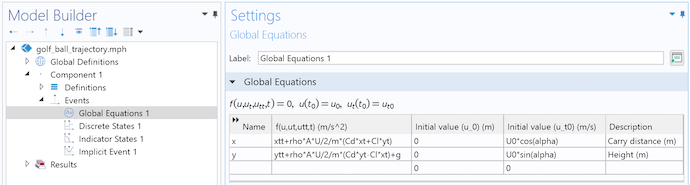
ボールの位置を解くグローバル方程式系.

次に，対応する初期条件を用いて, 式. 8の系を設定します. すべてのパラメーターと変数はすでに定義されているので, このステップは簡単です.

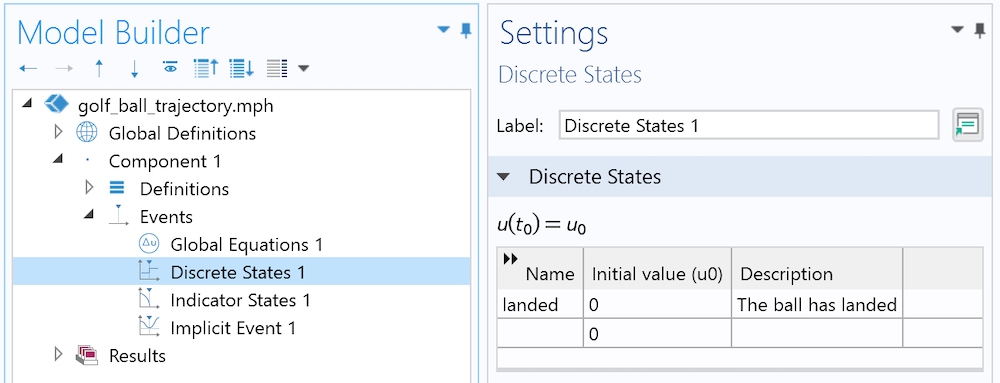
ボールが着地したかどうかを定義するには, 離散状態インターフェースを使用します.

以前のブログでご紹介したのと同様に, オン/オフの状態に最適な離散状態変数が追加されています. これは, ボールのグローバルな状態(着地したかどうか)を表しています. 初期状態では, ボールは着地していないとみなされるので, landed=0となります.

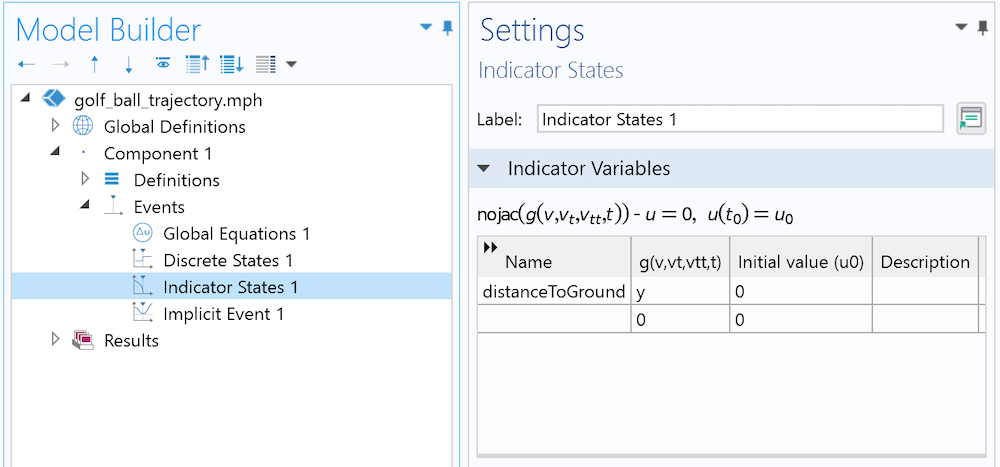
インジケーターの状態インターフェースは, 単純に現在の高さを表しています. 離散状態は, ボールが着地するとオンになります.

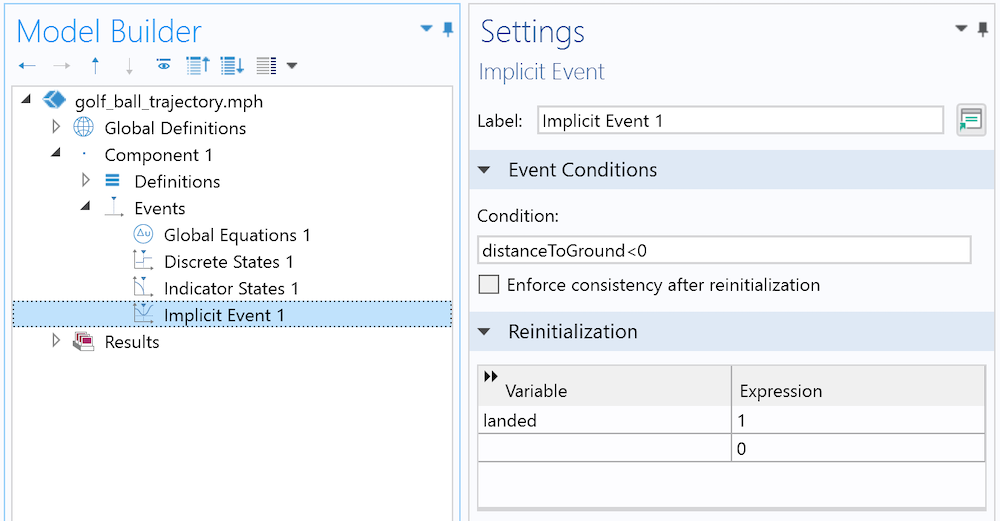
離散状態が更新されるのは, ボールが地面に触れたときだけです. このイベントがいつ発生するかは事前にわかりませんが, 数学的に変換することができます(高さがマイナスになります). これこそが, 暗黙的イベントノードの目的です. 指標となる状態(ここでは, 現在の高さ)がある条件を満たすと, イベントが発生するのです.

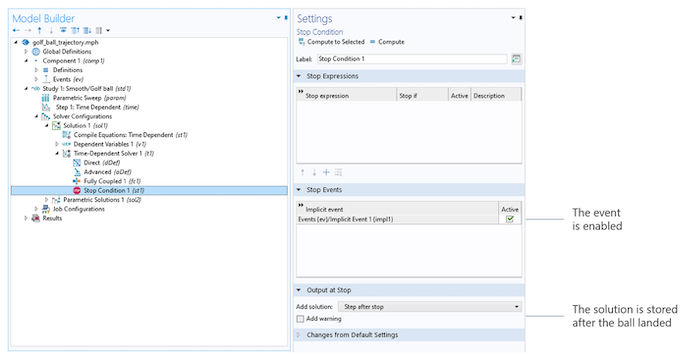
停止条件を追加するために, ソルバーシーケンスが変更されます.

最後のステップは, スタディノードの作成です. パラメトリックスタディを使用して, ゴルフボールと滑らかなボールを逐次計算し, 時間依存スタディを使用して

ボールの軌跡を解くことができます. イベントがアクティブ化されたときに計算を停止するには, 時間依存スタディのソルバーシーケンスを変更する必要があります.

シミュレーション結果

すべての設定が完了したので, 実際にシミュレーションを行ってみましょう!

7番アイアンで打ったゴルフボールと滑らかなボールの弾道をリアルタイムでアニメーション化したもの. ディンプルのあるボールは, 滑らかなボールに比べて抗力がはるかに小さいことがわかります(色の凡例は抗力係数を示しています). ボールは, 速度(したがってレイノルズ数)が低い軌道の上部で抗力の危機を経験することにご注目ください.

軌道の形は, 抗力や揚力を無視した場合に見られるような放物線ではないことにご注意ください. ボールは最初にほぼ直線的に上昇し, 最大の高さに達した後に急激に下降します. この結果から, ディンプル付きのボールは, 滑らかなボールに比べて25％(30メートル(33ヤード))進んでいることがわかります. 言い換えれば, グリーンはより近くなり, 追加の力は必要なかったということです!

これは, ボールの動きに逆らう抗力が, (冒頭で述べた理由により)ゴルフボールでの方が飛行中ずっとずっと小さいからです. ボールの高さが最大になると, 高さに比例する位置エネルギーも最大になります. このエネルギー移動は, 運動エネルギーを犠牲にして行われるため, ボールの速度は遅くなるのです. そのため, レイノルズ数が減少し(または同等にスピン係数が増加し), その結果, 抗力が増加します.

絶対的なキャリーは約150 m(165 yds)で, これは平均的なプレイヤーの典型的なゴルフショット (128 m(140 yds))よりもはるかに大きいですが, PGAプレイヤーの典型的なショットの下限にあります. この結果は, 抗力と揚力のデータが最新のゴルフボールから得られたものではないことを考慮すると, 妥当なものと言えます.

最適な打ち出し角度を見つける

ゴルフボールにディンプルを付けると, より遠くに飛ぶという効果があることはお分かりいただけたと思います. しかし, これを理解していても, 実際にどのようにボールを打てばよいのかはわかりにくいです. シャフトの速度とアタックアングルが一定であると仮定した場合, ボールの飛距離を最適化するためには, どのような打ち出し角度にすればよいのでしょうか. 最初のアプローチとしては, この値を見つけるために, パラメトリックスタディ, あるいは最適化スタディを行います. ここでは, あるアタックアングとスピンレートでの打ち出し角度によるキャリーの変化をグラフにしてみました.

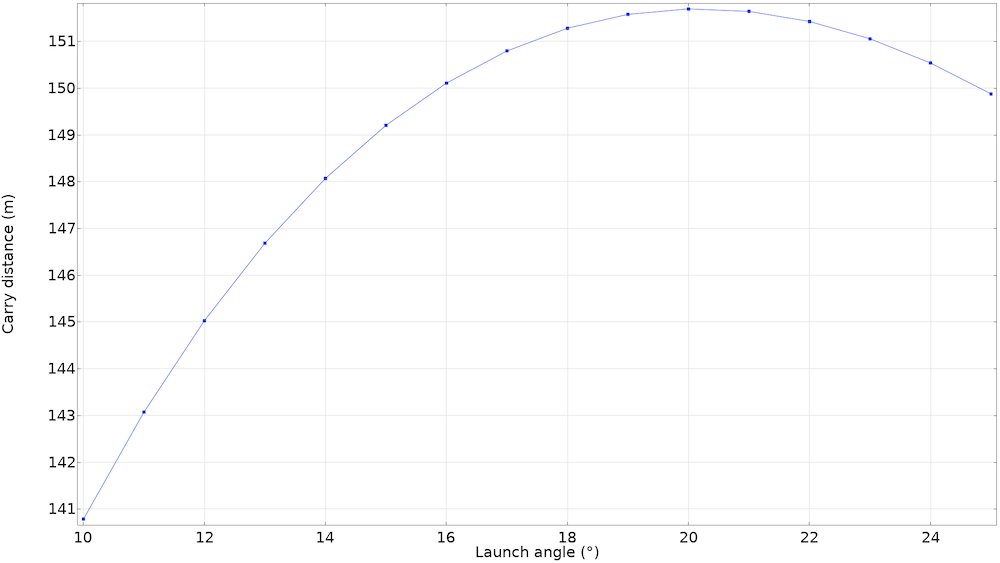
7番アイアンでアタックアングルを-4.3°, 初期スピンを6113rpmとした場合の, パラメトリックスタディの結果. 最適な打ち出し角度は20°前後のようですね.

この図を見ると, 最適な打ち出し角度は20°前後であるように思えます. しかし, 理論的には平均して最適な角度に近づくはずのPGAゴルファーたちは, 平均して16°の角度でショットしています. これはなぜでしょう? スピンレートが一定であるという私たちの仮説は間違っているのです. より大きな打ち出し角でボールを打つということは, クラブフェースを「より水平」にしてボールを打つ必要があります. テニスの「スライス」と同じように, ゴルフボールは摩擦が大きいために速く回転しますが, スピードは遅くなります.

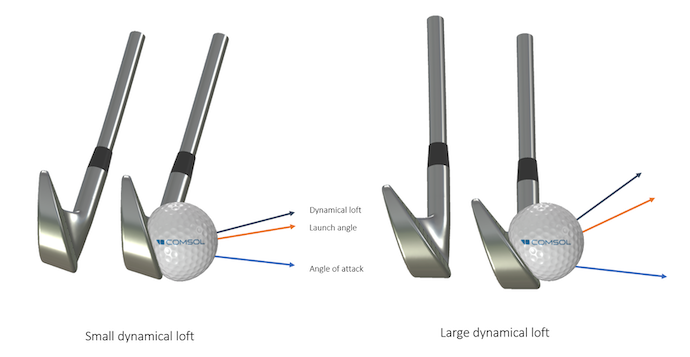
一定のアタックアングルに対する2つのダイナミックロフトの比較. 角度は水平線を基準にして測定されています. ダイナミックロフトが大きくなると打ち出し角が大きくなります. ダイナミックロフトとアタックアングルの間の角度(スピンロフトと呼ばれることが多い)が大きくなると, ボールの回転が速くなります.

打ち出し角度, スピンレート, ボールの速度の関係は直接的なものではなく, 実験やシミュレーションの結果を必要としません. ここでは, せっかくゴルフボールのモデルを用意したので, それをパラメータ化して使ってみましょう.

チュートリアルモデルのパラメーター化されたバージョンの結果. ポイントは3次スプラインを用いて補間され, より滑らかな曲線になっています. 予想通り, スピンレートは打ち出し角度が大きいほど増加し, 速度は逆の挙動を示しています.

この結果は慎重に見ていかなければなりません. メッシュの収束性のスタディ, 他のシャフトの曲線との比較など, より詳細なスタディを行う必要があります. とはいえ, この結果は十分に現実と一致しています.

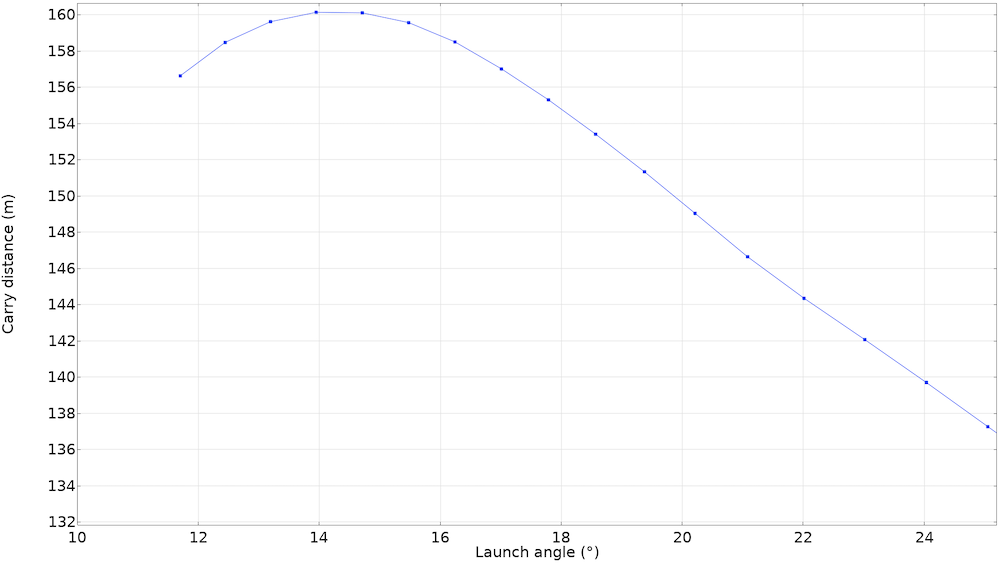
一定でないスピンで-4.3°のアタックアングルの打ち出し角度に対する, 7番アイアンのキャリー. 実際の挙動をよりよく捉えるために，曲線は打ち出し角の低い値にシフトされています.

これで, 正しいスピンと速度の値でパラメトリックスタディを再度実行することができます. 曲線が左にシフトしていることにご注目してください. 言い換えれば，打ち出し角を小さくすると(したがって，ダイナミックロフトを小さくすると), スピンレートが減少し, ボールの並進運動エネルギーが高くなるということです. この曲線は, 予想通り16°を中心としたものではありません. しかし，この結果を得るためには，最終的な結果に大きな影響を与える多くの仮説(抗力と揚力の分布やスピンレートの依存性など)が立てられています. より正確な結果を得るためには, 最新のゴルフボールのデータやボールの衝撃の解析が必要です.

まとめ

今日のブログでは, 特定の範囲のレイノルズ数における球体上の乱流境界層の挙動に関する, ゴルフボールのディンプルについての一見単純な質問に答えました. これは, エンジニアリングにおける古典的なプロセスの概要でもあります. 一般的な物体を観察することで, 複雑な物理現象をより深く理解することができ, その結果, COMSOL Multiphysics を使っていくつかの仮定の下でモデル化し, 検証することができました. 最終的には, 最適な打ち出し角度を見つけ出し, 実社会に役立つ情報を引き出すことができました.

私と同じような疑問を持ったことがあるゴルファーの皆さんに覚えておいていただきたいことは, スピンレートを減らすために, 同じアタックアングルを維持したまま, ダイナミックロフトを下げてみることです. シミュレーションの結果を見ると簡単そうですが, 実際にフェアウェイで実行するとなると難しそうです. ですから, このブログの本当の教訓は, シミュレーションエンジニアではなく, プロのゴルフ教師に聞くことです!

自分で試す

COMSOL Multiphysics でゴルフボールの軌道を計算してみましょう. 下のボタンをクリックすると, このブログで紹介されているモデルファイルにアクセスできます.

参考文献

1. P. Bearman and J.K. Harvey, “Golf ball aerodynamics”, Aeronautical Quarterly, vol. 27, no., pp. 112–122, 1976.
2. A.J. Smits and D.R. Smith, “A new aerodynamic model of a golf ball in flight”, Science and Golf II, Taylor & Francis, pp. 433–442, 2002.