構造トポロジの最適化
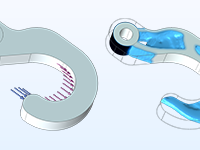
フックのトポロジ最適化. 与えられた総重量に対して, 最適なコンプライアンスが得られるように材料を配分します.
マルチフィジックスモデルの最適化
COMSOL Multiphysics® のアドオンである最適化モジュールは, パラメーター, 形状,トポロジの最適化, およびパラメーター推定のためのツールを提供します. COMSOL 製品の他のモジュールと一緒に使用すると, 電磁気学, 構造力学, 音響学, 流体の流れ, 熱伝達などの現象を伴うデバイスとプロセスを最適化できます. CAD インポートモジュール, 設計モジュール,または CAD 用の LiveLink™ 製品のいずれかと組み合わせると, 幾何学的寸法を最適化できます.
改善すべき目的関数と変更すべき設計変数, およびオプションの制約条件を指定すると, 最適な設計が探索されます. モデルへの入力は, 幾何学的寸法,部品形状, 材料特性, 材料分布のいずれでも設計変数として扱うことができ, モデルの出力は目的関数として使用でき, 最小化または最大化することができます.
COMSOL へお問い合わせ
最適化モジュールを COMSOL® アドオン製品のいずれかと組み合わせて, いくつかの異なる物理領域内で最適化を実行します.

フックのトポロジ最適化. 与えられた総重量に対して, 最適なコンプライアンスが得られるように材料を配分します.
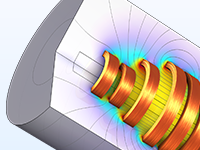
10ターンコイルのパラメーターと形状を最適化し, 磁束密度と損失電力を最適化.
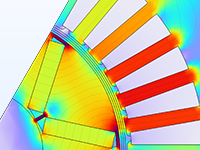
トルクに応じた永久磁石の最適な位置, 形状を特定する電動機のパラメーター最適化.
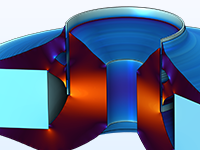
大変位非線形応答を低減するためのスピーカードライバーで使用される磁気回路のトポロジ最適化.

スピーカーのツイータードームと導波管の形状最適化により, 応答曲線の平坦化と放射パターンの改善を実現.
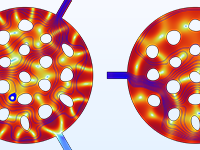
音響デマルチプレクサーの形状最適化. 音響エネルギーは周波数帯ごとに異なる出力ポートに送られます.
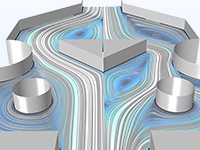
テスラマイクロバルブの形状とトポロジの最適化により, 双方向の流れに対する圧力損失の比率を最大化します.
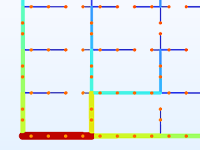
地域暖房ネットワークレイアウトのトポロジ最適化.
COMSOL Multiphysics® は, さまざまな種類の最適化に対して, 専用のソルバーでカスタマイズされたユーザーインターフェースを提供します.
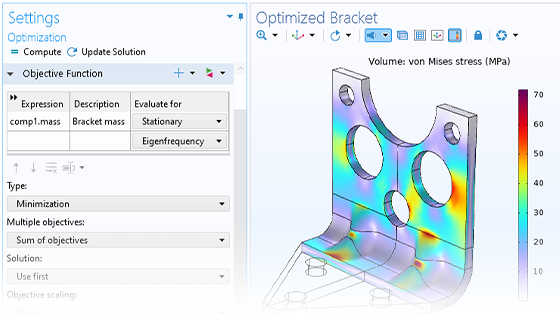
COMSOL Multiphysics® でパラメーター最適化を設定するには, 汎用の最適化スタディを追加するだけです. 関連する設定ウィンドウでは, 目的関数, 制御変数とパラメーター, および制約を追加するように求められます. パラメーター最適化では, ジオメトリの寸法, 材料特性, 境界荷重など, 最初にモデルを設定するために使用したパラメーターを使用することができます. パラメトリックスイープでは設計パラメーター空間についての大まかな情報が得られますが, パラメーター最適化では最適なパラメーターと目的関数値を取得することができます.
ジオメトリの寸法を定義するパラメーターを使用してパラメーターの最適化を実行する場合, 反復ごとに再メッシュが必要です. これは, 最適化モジュールで完全に自動化されたプロセスです. 最適な解は常に, 業界標準の CAD 形式にすぐにエクスポートできる真の CAD パーツです. これには, CAD インポートモジュール, デザインモジュール, または CAD 用の LiveLink™ 製品の1つが必要です.
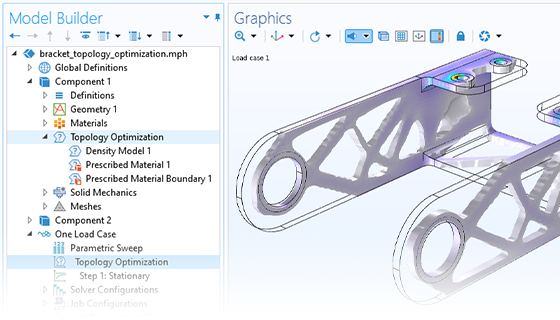
トポロジ最適化は, パラメーターと形状の両方の最適化よりも, ジオメトリの変化の自由度がさらに高くなります. このアプローチにより, 最適化プロセス中に材料の除去と追加が可能になり, 設計に元々存在していなかったジオメトリに穴を作成できます. この方法は通常, 有機的なデザインになり, 軽量化のための一般的な方法です. トポロジ最適化には, 専用のユーザーインターフェースとスタディを利用できます.
形状最適化と同様に, トポロジ最適化には再メッシュは必要ありません. 最適で滑らかな設計は, STL, 3MF, または PLY ファイル形式で利用可能になり, 別のソフトウェアでさらに使用したり, COMSOL Multiphysics® 内の検証解析に使用したりできます.
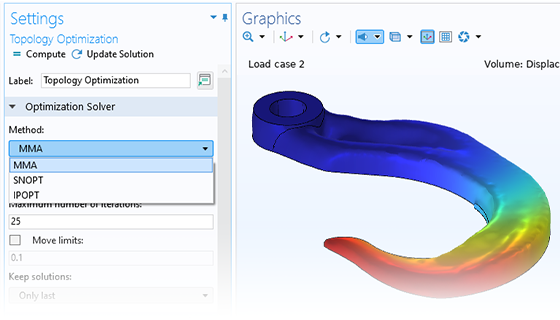
勾配ベースの最適化手法は, 随伴法を使用して導関数を効率的に計算できる場合に使用されます. これは, これらが区別可能である限り, カスタムの目的関数または制約に対して可能です. これは, シンボリック微分を特徴とする COMSOL Multiphysics® のコアテクノロジーのおかげであり, カスタムマルチフィジックス問題を求解するために必要な柔軟性も提供します.
勾配ベースの最適化は, 数千, さらには数百万の設計変数で使用できます. これは, 形状またはトポロジ最適化の場合によくあります. 設計変数は, 空間全体に分散され, 各メッシュ要素の異なる値で表される場の量を表します.
勾配ベースの方法は, すべての解析導関数を同時に計算しますが, 導関数を使用しない方法は, 各導関数を近似する必要があり, 設計変数の数が増えるにつれて時間がかかります.
最適化モジュールに含まれる勾配ベースの方法は次のとおりです.
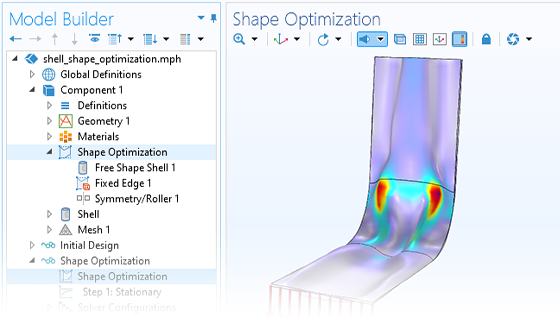
CAD パラメーターのセットを変更する代わりに, 形状最適化の組み込み機能を使用して, ジオメトリを多少自由に変形させることができます. このアプローチにより, 自由度が高まり, パラメーター最適化よりも優れた結果が得られる場合があります. 2D または 3D モデルで許容される境界の変形を簡単に定義するために, 専用のユーザーインターフェースのセットを使用できます. さらに, 特殊なシェル形状最適化機能, およびソルバーを制御するための形状最適化スタディタイプを使用できます.
ソリッドの形状最適化に使用されるツールは, 再メッシュが不要な制御された方法でメッシュを変形する方法に基づいています. 最適なジオメトリは, STL, 3MF, PLY などのファセットサーフェスメッシュ形式で利用できます. このジオメトリは, COMSOL Multiphysics® 内の別の解析で再利用したり, 別のソフトウェアで使用するためにエクスポートしたりできます.
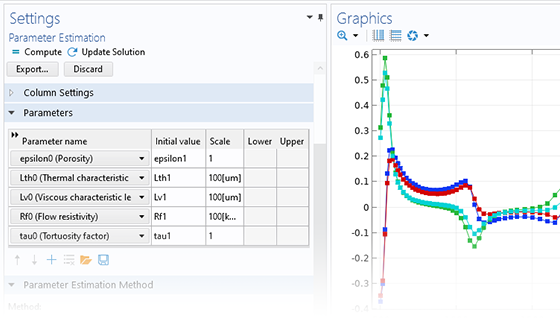
モデルは入力と同じくらい正確ですが, サプライヤーから正確な材料パラメーターを入手するのは難しい場合があります. 非線形性を説明するために, 実験を実行する必要がある場合があります. ただし, 解析手法を使用して目的のパラメーターを抽出できる実験を計画することは困難な場合があります.
これらの問題の解決策は, 最適化モジュールのパラメーター推定機能を使用して, 物理実験とシミュレーション実験の間の偏差を最小化するモデルのパラメーターのセットを見つけることです. 一般的なパラメーター推定用のインターフェースに加えて, 曲線 (モデル式で表される) を時間依存データにフィッティングするための曲線フィッティング専用のユーザーインターフェースを使用できます.
パラメーター推定法は最小二乗フィッティングに基づいており, 参照データが時間の関数または単一のパラメーターである場合に使用できます. 多くの場合, 推定されたパラメーターの分散と信頼度の推定値が得られます.
パラメーター推定を開始するために, 組み込みのチュートリアルサンプルまたはインポートされた測定データを使用したり, フィットする曲線のカスタムモデル式を入力したりできる, すぐに使用できるアプリを利用できます.
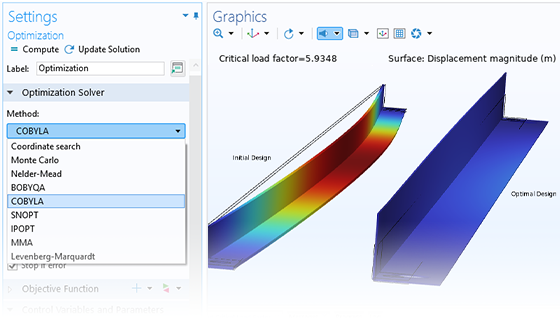
最適化ソルバーに必要な検索方向を間接的にしか計算できない場合は, 導関数のない最適化手法が使用されます. これは, 制御変数がジオメトリ寸法を表し, 各反復ステップで再メッシュが必要なパラメーター最適化の場合によくあります.
最適化モジュールに含まれる微分なしの方法は次のとおりです.
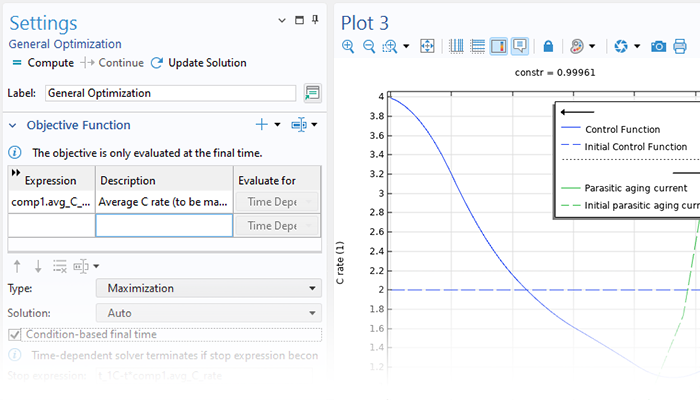
プロセスの所要時間はコストと密接に関係していることが多く, 時間を最小化することでコスト削減につながる場合があります. 一方で, 製品の劣化や分解のように, プロセス時間を最大化することが有益な場合もあります.
最適化モジュールには, 一般的な最適制御問題の定式化に対応した組み込み機能が用意されており, 最適化された制御値の正則化と便利なエクスポート機能も含まれています. この機能により, 問題の設定, 求解, そして得られた結果をより大規模なシミュレーションやワークフローで再利用することが容易になります.
最適制御および時間最適制御は, すべての最適化ソルバーでサポートされています. ただし, 大幅な性能向上を得るには多くの調整可能なパラメータが必要になることが多く, そのような場合には勾配ベースの最適化手法を用いるのが最も適しています.
アプリケーションビルダーと最適化モジュールを併用することで, シミュレーションの専門家に相談することなく, より多くのユーザーが独自に最適化研究を行うことができるようになります.
例えば, 最適化モデルには実験データに基づくパラメーター推定が含まれます. このようなタスクに特化したアプリケーションを使用すると, ユーザーは最適化モデル自体の詳細を気にすることなく, さまざまな実験データを入力することが可能になります.
また, アプリを利用することで, 最適制御のワークフローをより効率的に行うことができます. 最適化モジュールは, どの過渡入力が望ましい過渡出力を与えるかを特定するために使用することができます. この場合, 実験結果に基づいて望ましい出力を調整したい場合があります. このタスクのためにアプリを作成することで,このプロセスの複雑さをカスタムユーザーインターフェースにパッケージ化し, さまざまなユーザーが希望の出力を指定するだけで最適制御シミュレーションを実行できるようになります.
シミュレーションのニーズはそれぞれ異なります.
COMSOL Multiphysics® ソフトウェアがお客様のご要望を満たすかどうかをきちんと評価するために, ぜひ当社までお問い合わせください. 営業担当者との打ち合わせを通じて, 各個人に向いたお勧めや文書化されたモデル事例などをお送りすることができ, 最大限の評価結果を引き出すことができます. 最終的にどのライセンスオプションがあなたの要望にとって最適かを選択することができます.
"COMSOL へお問い合わせ" ボタンをクリックしてください. あなたの連絡先情報およびご意見やご質問をご入力のうえ送信してください. 1営業日以内に営業担当者よりご連絡いたします.
ソフトウェアデモをリクエスト