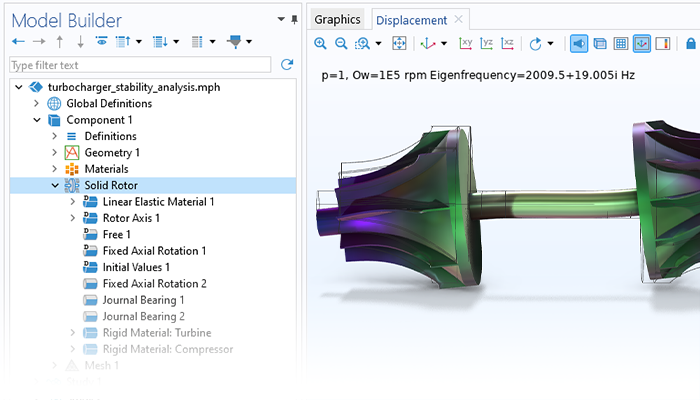
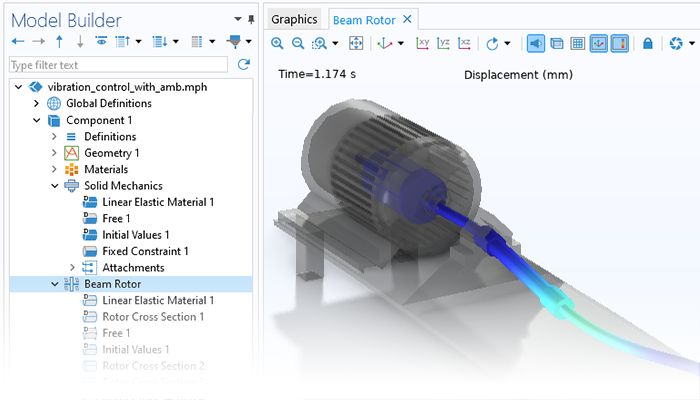
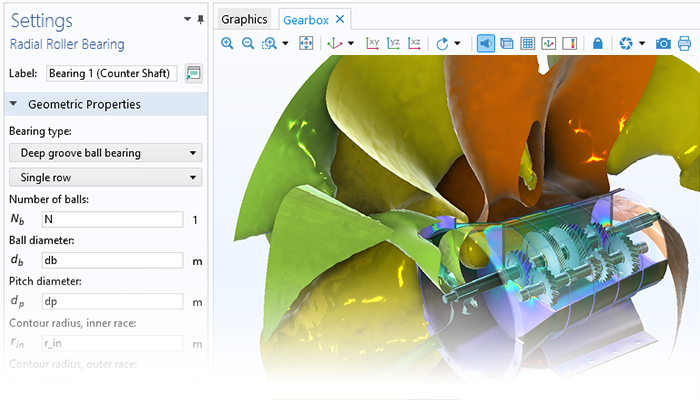
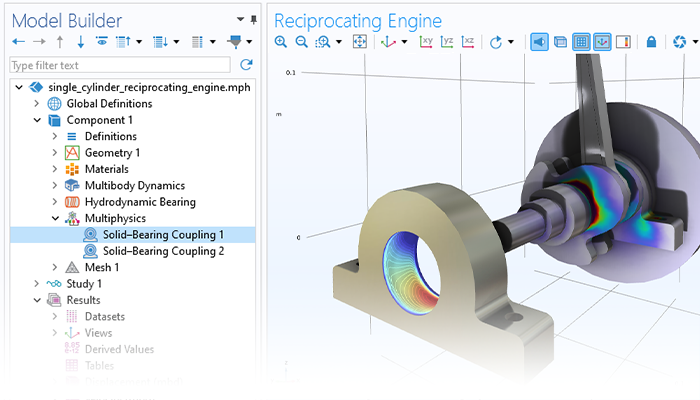
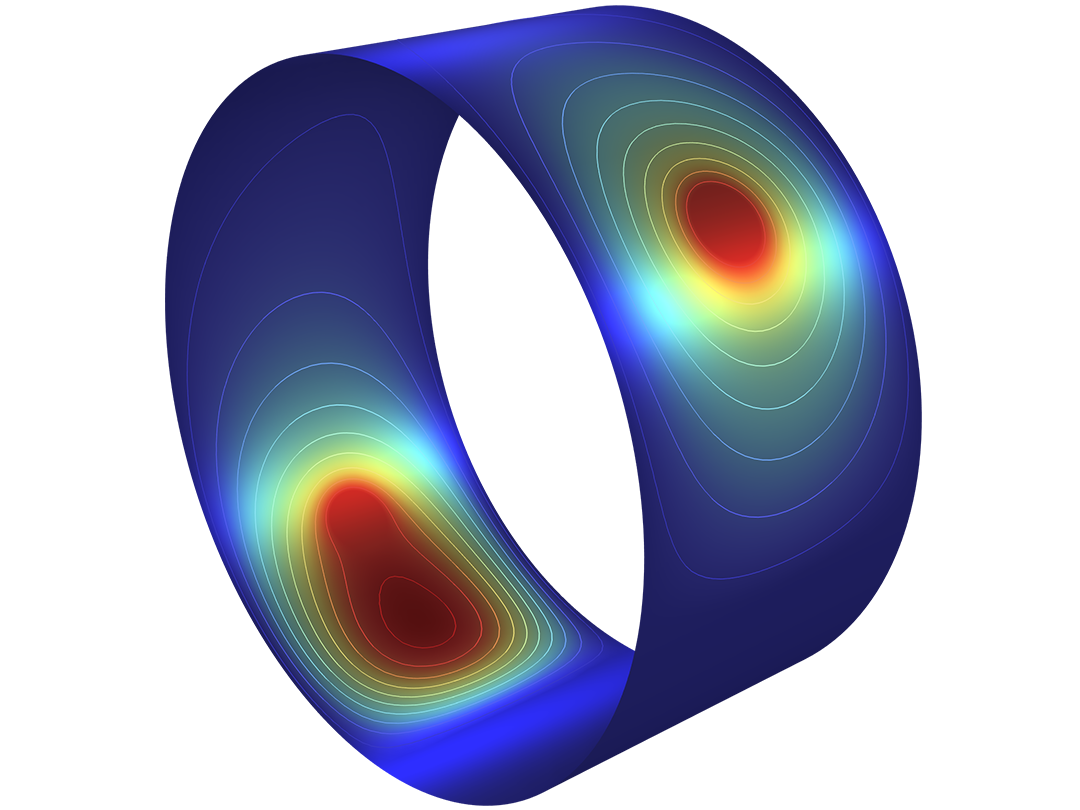ローター軸受システムの解析
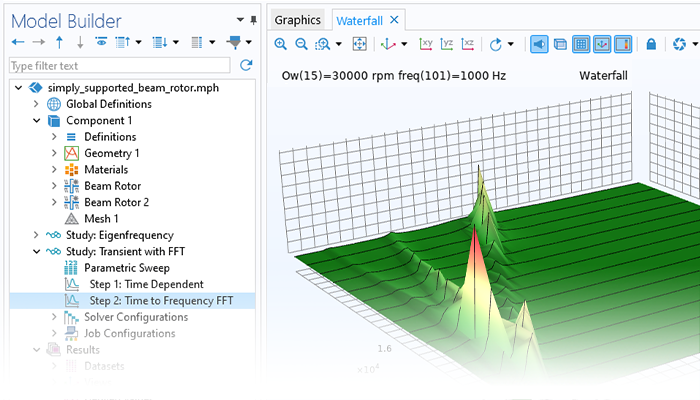
回転機械の物理的挙動は振動に大きく影響され, 機械自体の回転や形状によって振動はさらに大きくなります. 完全に対称なローターアセンブリでさえ, 回転速度の増加とともにモード分離が発生します. これは, 垂直対称面における同一モードの通常の挙動が, 回転シャフトには適用できないことを意味しています. さらに, 回転システムの固有振動数に近い周波数で動作する場合, わずかな欠陥や不均衡であっても, 大きな振動振幅を引き起こす可能性があります.
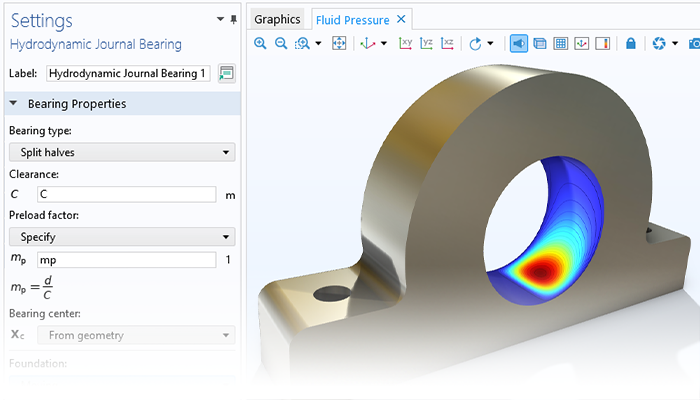
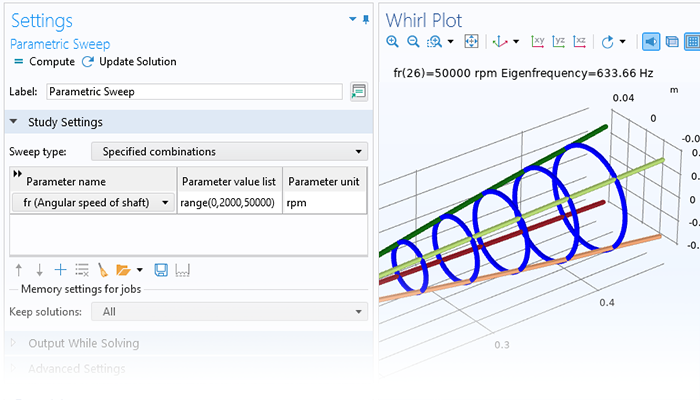
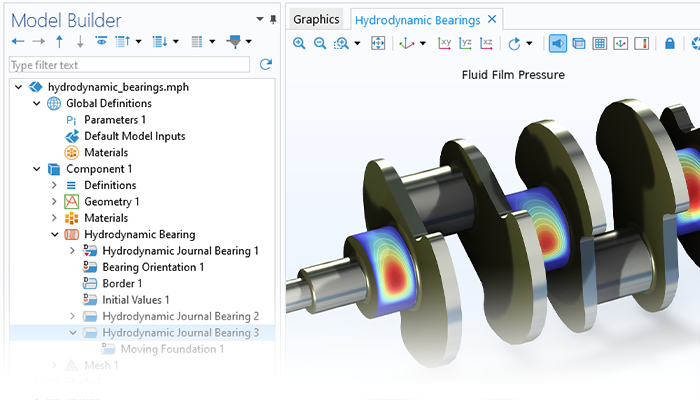
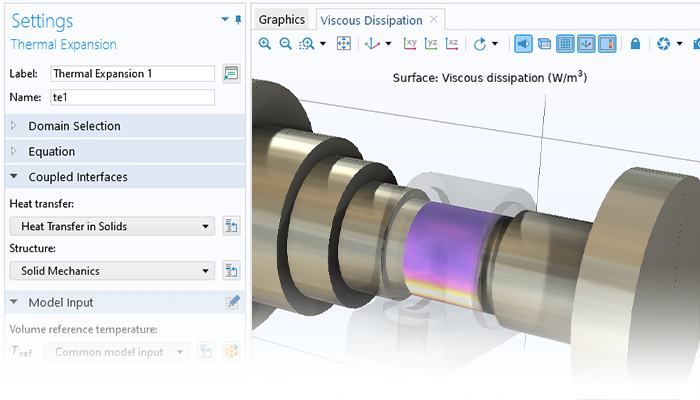
ローターダイナミクスモジュールを使用すると, ローター, 軸受, ディスク, およびファンデーションにおける共振, 応力, およびひずみの解析が可能になるため, ユーザーは条件を許容可能な動作限界内に保つことができます. また, このモジュールを使用して, 異なる設計パラメーターが固有振動数にどのように影響し, その結果として臨界速度, 旋回, および安定性のしきい値にどのような影響を与えるかを評価することもできます. さらに, 定常および過渡的なアンバランス応答を調査するためにも使用できます.
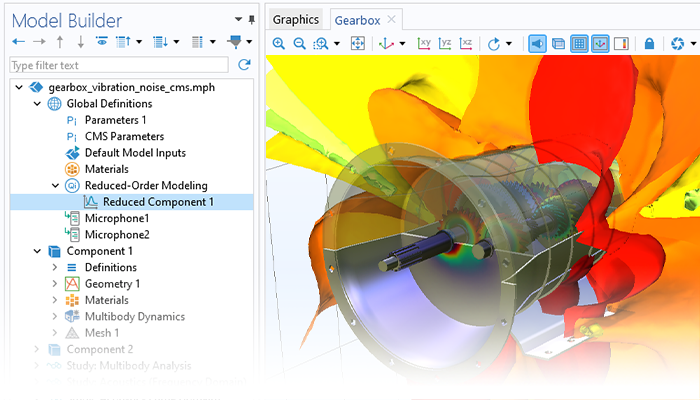
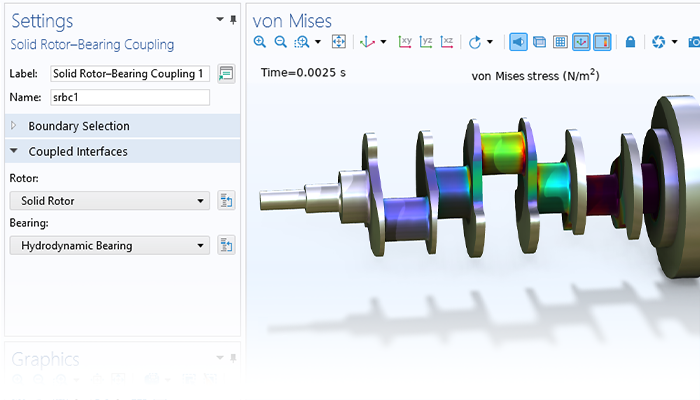
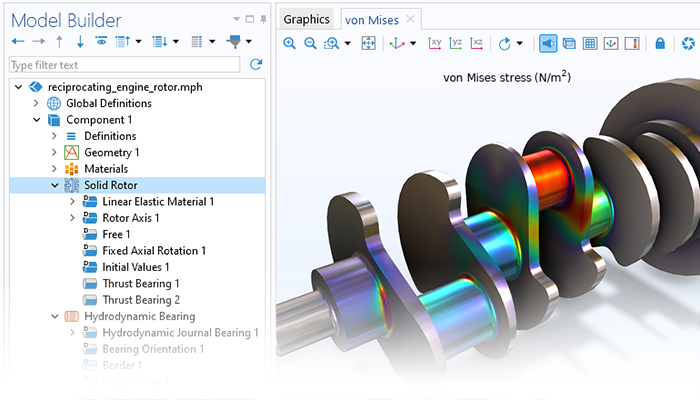
このモジュールはまた, 回転挙動がローター自体の応力にどのように影響し, 回転機械のアセンブリの他の部分に負荷や振動がどのように伝達されるかを予測するための機能も備えています.