
COMSOL Multiphysics® ソフトウェアには, 自由液体表面をモデル化するための4つの方法があります. レベルセット, フェーズフィールド, 移動メッシュ, および静止自由表面です. このブログシリーズの最初の部分では, レベルセット法とフェーズフィールド法について説明します. これらは, ほぼすべての種類の自由液体表面を記述するフィールドベースの方法です. パート 2 では, この投稿の結果と, 自由表面の問題を求解するために 移動メッシュ インターフェースを使用して得られた結果を比較します.
レベルセット法とフェーズフィールド法とは?
レベルセット法とフェーズフィールド法はどちらもフィールドベースの方法で, 自由流体表面がレベルセット関数またはフェーズフィールド関数の等値面として表されます. 自由液体表面は, 液体とガスの間の相境界に対応し, 固定メッシュ上に表されます.
下の図は, 流路内の2つの液滴の表面を示しています. これは, アドオン マイクロフルイディクスモジュール のアプリケーションライブラリにある液滴分解モデルから取得したものです. このプロットでは, 液滴の表面は非常に鋭いものの, 液滴の周囲の要素は液滴の表面に付着していないことがわかります.
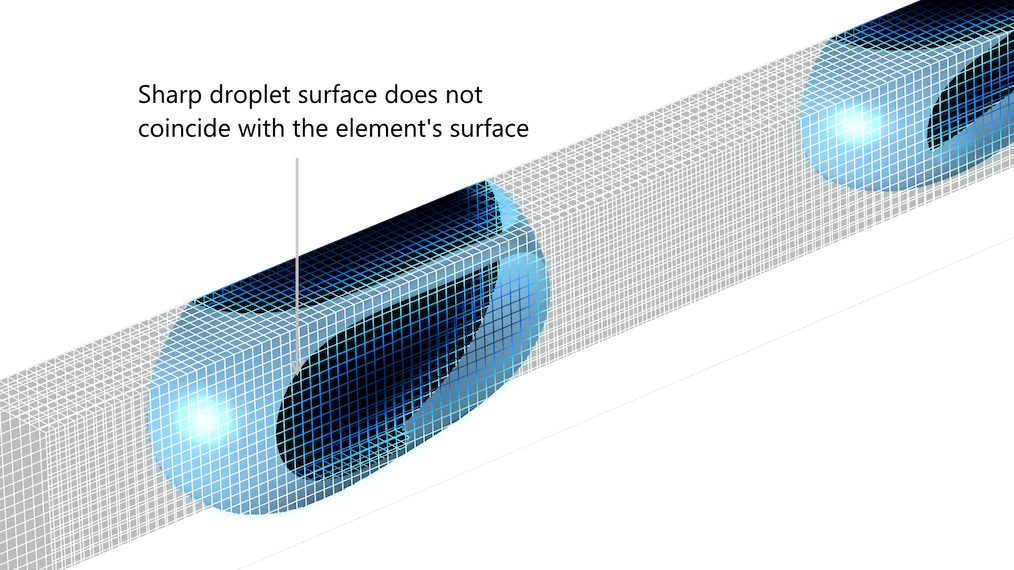
液滴表面は, レベルセット法でもフェーズフィールド法でも, 要素の表面と一致しません.
レベルセット関数とフェーズフィールド関数はどちらも, ナビエ・ストークス方程式 によって計算された速度ベクトルによって移流されます. レベルセット法とフェーズフィールド法の両方で, これは次のようになります:
(1)
レベルセット関数とフェーズフィールド関数の両方に Φ を使用していることに注意してください. 方程式の右側の F は, 2つの方法が異なる部分です. 元のレベルセット法では, F = 0 であり, 純粋な移流輸送方程式が得られます. ただし, F = 0 の数値解は不安定で, ほとんどの場合, 実用性はほとんどありません. 代わりに, 界面コンパクトに保つように設計された Φ の高次導関数を持つ項が, レベルセット法の F に導入されています.
フェーズフィールド法では, F はシステムの自由エネルギーを最小化しようとする項を表します. また, Φ の高次導関数がこの項に導入されています. 実際, フェーズフィールド方程式のソース項には4次の項が含まれています. つまり, 実用的な理由から, 方程式は2つの方程式に分割されることが多く, 補助従属変数は Φ の2次導関数の関数として定義されます. これは COMSOL Multiphysics でも行われていることです.
どちらの方法でも, 自由液体表面の表面張力から生じるナビエ・ストークス方程式にソース項が導入されます. レベルセット法では, 自由境界を表すレベルセット等値面の曲率を使用して表面張力を記述します. フェーズフィールド法では, 表面張力によるナビエ・ストークス方程式への寄与は化学ポテンシャルから計算され, 表面張力と界面近くのフェーズフィールド関数の勾配が得られます.
流体の特性は, レベルセット関数またはフェーズフィールド関数の特定の値, つまり自由表面を表す値を超えて, 液体から気体へとスムーズに遷移します.
レベルセット関数 Φ は, 自由表面全体で 0 から 1 の間で変化し, 2つの流体のバルク内では 0 または 1 で一定です. レベルセット関数は, たとえば, 液体の場合は 0, 気相の場合は 1 になります. 自由液体界面, つまり液体と気体の相境界は, レベルセット関数 Φ の値 = 0.5 に対応します. したがって, 密度はレベルセット関数の関数であり, 次の式に従います:
(2)
動的粘度も同様です:
(3)
上記の2つの式から, Φ = 0 のときは流体 1 (たとえば液体) の特性が得られ, Φ = 1 のときは流体 2 (たとえばガス) の特性が得られることがわかります. 自由表面を横切る流体特性の滑らかな遷移, つまりレベルセット関数と同じくらい滑らかな遷移が得られます.
フェーズフィールド関数 Φ は -1 から 1 の間で変化します. ここで, 自由液体表面は Φ = 0 の等値面です. 粘度と密度の計算はレベルセット法と類似した方法で行われますが, フェーズフィールド関数が -1 から 1 の間で変化するため, 式が異なります.
レベルセットおよびフェーズフィールドインターフェースの設定
レベルセット および フェーズフィールド インターフェースには, メソッドを最適に実行するために調整が必要なパラメーターが多数含まれています. これらのパラメーターの値は, モデル化された系と方程式の数値離散化によって異なります. ジオメトリのサイズ (長さ, 幅, 深さ), 流体の特性, 壁の濡れ, 初期条件, 動作条件, 作成されたメッシュ内の要素のサイズはすべて, モデル設定の選択に影響します.
レベルセットインターフェース
レベルセット法の設定から始めましょう. ユーザーインターフェースの再初期化パラメーター γ は, レベルセット関数の勾配が時間の経過とともに自由表面に集中するようにします. つまり, 以下の例では水と空気の界面に集中します. これは表面の厚さを設定するのではなく, レベルセット関数の変動がこの厚さ内に収まるようにします. この値を低く設定しすぎると, レベルセット関数の変動が流体の1つのバルクに閉じ込められ, 液体とガスの界面が突然作成されます. 値が高すぎると, 時間ステップが小さくなり, 計算時間が長くなる傾向があります.
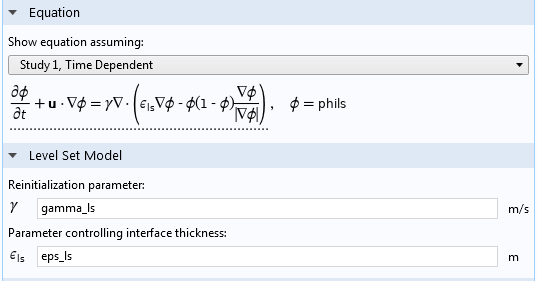
レベルセットインターフェースの設定ウィンドウ.
ユーザーインターフェースで ε と表示される界面厚みパラメーターは, より直感的に理解できます. これは, レベルセット関数の変動が取得される領域の厚さを制御するだけです. 厚さが厚いと, 自由表面の形状がぼやけます. 問題は解けやすくなりますが, 自由表面の形状の精度は失われます. ε の値が小さいと, 表面のコンパクトな表現が得られますが, メッシュの対応する解像度が必要になります. メッシュ要素のサイズよりもはるかに小さい値を設定すると, 界面が不規則になり, 未求解の表面張力によって誤った速度が発生する可能性があるため, 意味がありません. ε の値は, 表面に近い最大の要素とほぼ同じ値に設定する必要があります.
フェーズフィールドインターフェース
ここでフェーズフィールド法について見てみると, 界面厚みのパラメーター ε は, 上記のレベルセット法とほぼ同じであり, その値の選択にも同じ理由を適用できます.
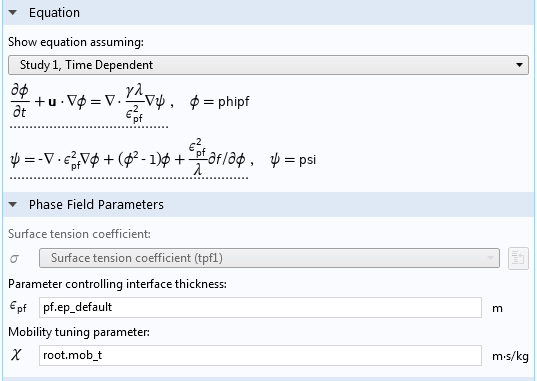
フェーズフィールドインターフェースの設定.
フェーズフィールド法の移動度調整パラメーターであるユーザーインターフェースの χ は, フェーズフィールドの拡散率を特定の方法で決定します. この値は, フェーズフィールド方程式が安定するのに十分な大きさで, かつ, シャープなインターフェースが得られるほど小さい必要があります. 適切な値は表面の速度に比例し, 表面張力の係数に反比例します.
(4)
つまり, 特定の動作条件セットに対して適切な χ の値を見つけたら, 上記の関係を使用して新しい条件セットに対して χ を設定できます.
自由液体表面のモデリング
以下の図は, COMSOL Multiphysics で自由表面をモデリングするためのレベルセット法とフェーズフィールド法を調べるために使用するサンプル問題を示しています.
固体の棒が小さな流路内の水に半分浸かっています. 棒は水面の接線方向に前後に動かされ, 水面に穏やかな波を発生させます. 流路と棒の寸法は, 流れを層流に保つのに十分小さいです.
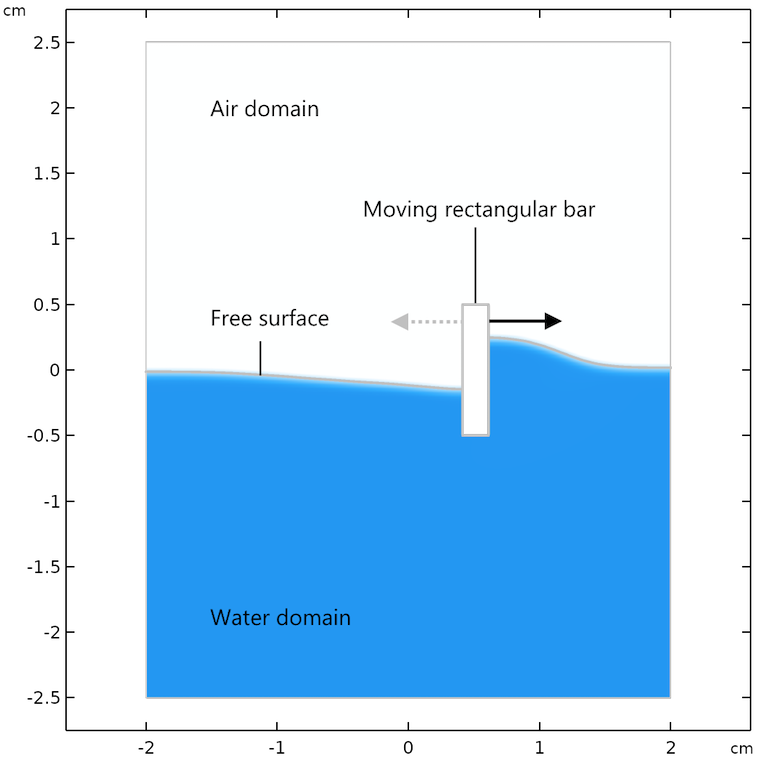
例題のジオメトリと定義.
移動メッシュ機能は, 小さな長方形の棒が表面上を前後に動くように指定するために使用されます. ただし, レベルセット法とフェーズフィールド法では, メッシュは液体表面とともに移動しません.
COMSOL Multiphysics でのモデル実装に関する注意点をいくつか示します.
- 運動量方程式のソースとして重力を追加します
- 圧力場の参照と点制約を追加します
- 結果を比較するために, 壁にナビエすべり条件を選択し, 要素の長さと同じサイズのスリップ長を使用します
レベルセット法とフェーズフィールド法のシミュレーション結果
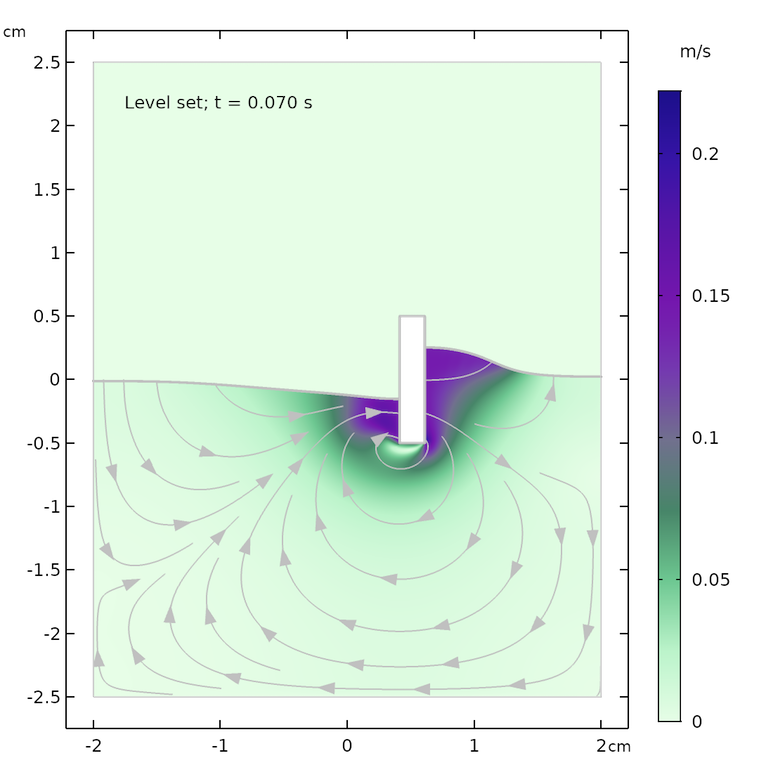
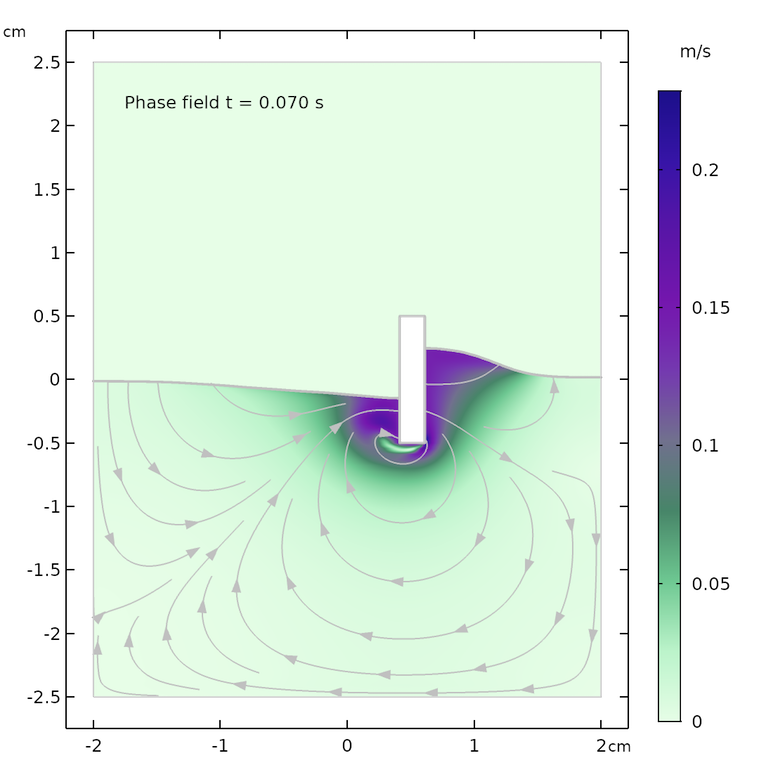
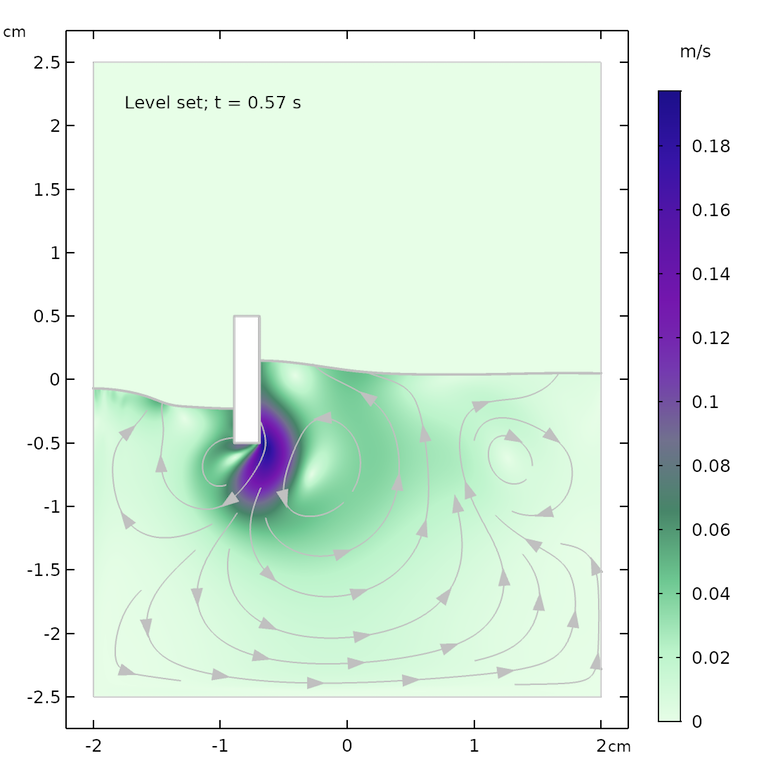
以下の時間における流れ場と水面の形状の結果を示します: 0.07 秒, 0.57 秒, 1.0 秒. それぞれの時間における両方の方法で, 流れの流線と水面の形状はほぼ一致しています. 最大速度と水面の高さにわずかな違いがありますが, これは2つの方法で表面張力の扱いが異なるためと考えられます.
また, 時間が経過した後の流線にも, たとえば t = 1.0 秒の再循環ゾーンでの違いが見られます. フェーズフィールド法では, 表面の挙動がやや穏やかになる傾向があります. レベルセット法では, レベルセット関数の勾配から得られる表面の曲率から表面張力を計算します. これにより, フェーズフィールド法で得られる滑らかな力と比較して, より “スパイク状の” 表面力が得られます.
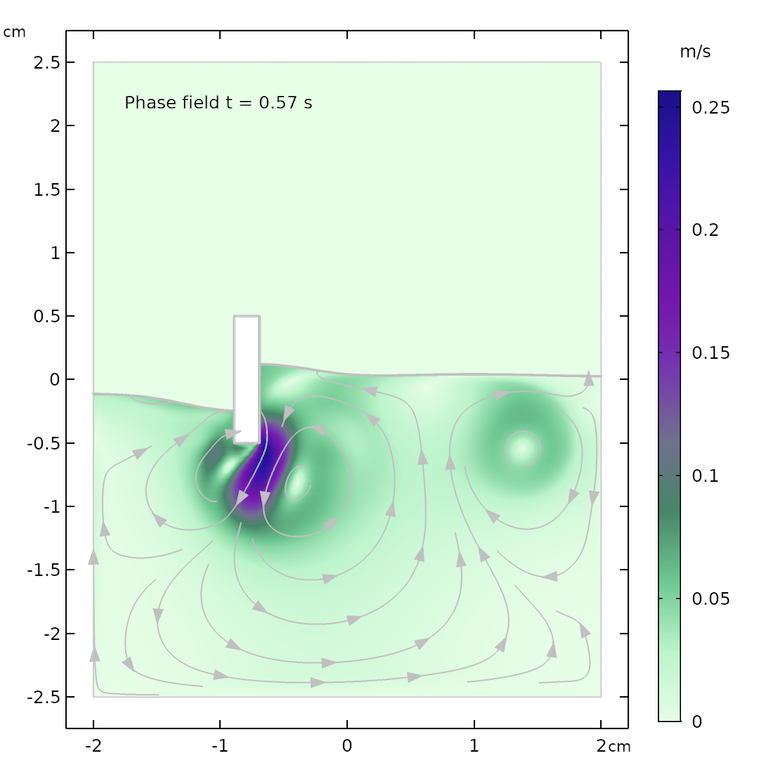
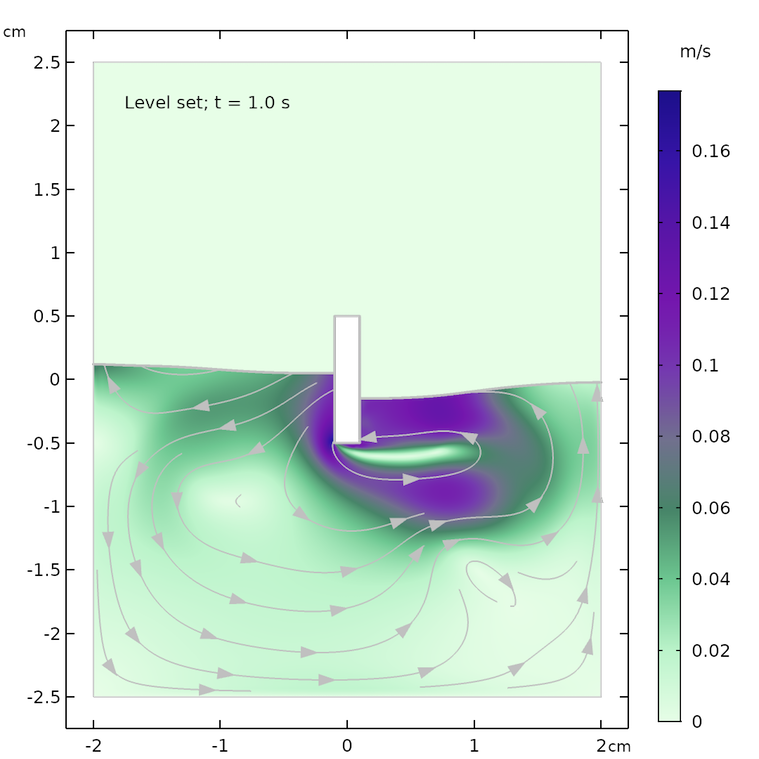
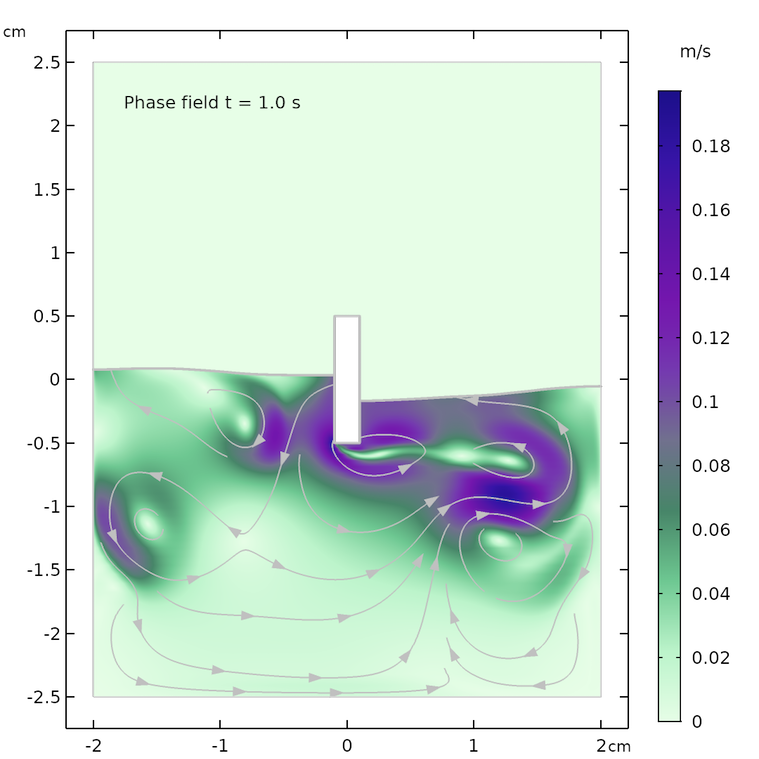
レベルセット法 (左) とフェーズフィールド法 (右) の結果. 0.07 秒 (上), 0.57 秒 (中央), 1.0 秒 (下) 後.
シミュレーションの完全な結果を0秒から2秒までのアニメーションで可視化することもできます. 長方形の棒の動きによって激しい攪拌が起こりますが, 自由表面が壊れないことがわかります.
フェーズフィールド法を使用して問題の解から作成されたアニメーション.
レベルセット法とフェーズフィールド法では, 自由液体表面上の空気領域の流れ場も計算されます. 長方形のバーの動きによって, 相の界面上で連続した活発な流れ場パターンが生成されることがわかります.
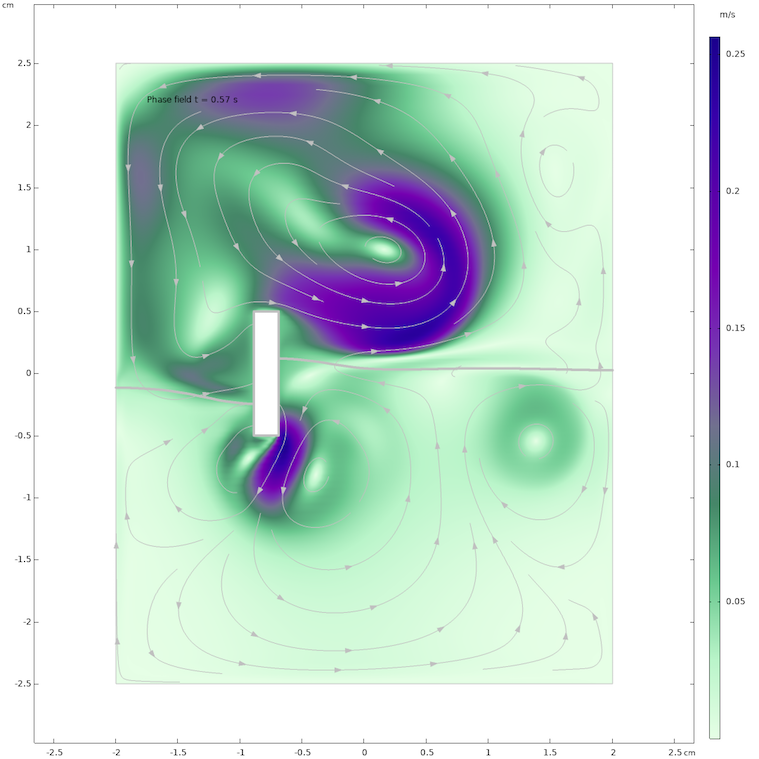
フェーズフィールド法で計算された, 0.57 秒後の水と空気の領域の流れ場.
表面の攪拌が激しくなるように増加すると, 表面が分解して後で合体することがあります. これは, 下のアニメーションに示されています. これは, レベルセット法とフェーズフィールド法の利点の1つでもあります. この2つの方法のいずれでも, 自由表面のトポロジの変化に対処するのは比較的簡単です.
長方形のバーによる撹拌は, 小さな波が砕けて水相に閉じ込められた空気ポケットが生成されるまで, 周波数と振幅の両方が増加します.
レベルセット法とフェーズフィールド法は似ていますが, 少なくとも COMSOL Multiphysics での実装では, 表面張力の扱いが2つの方法の安定性に大きな影響を与えます. 表面張力の強い影響を伴う問題の場合, フェーズフィールド法は, レベルセット法と比較して, 計算時間に関して優れたパフォーマンスを示します. この違いの理由は, レベルセット法での表面曲率の計算により, 時間依存ソルバーがフェーズフィールド法と比較して大幅に小さな時間ステップを実行する必要があるためです.
この例では, フェーズフィールド法では時間ステップが平均で5倍大きくなり, その結果, レベルセット法の計算時間が5倍長くなります. したがって, 小規模の自由表面問題や, 表面張力が大きな影響を与える層流 (マイクロ流体など) の場合, 一般的にフェーズフィールド法の方が適しています.
アダプティブメッシュ細分化と自由表面
このブログで調査した2Dの例では, レベルセット法とフェーズフィールド法で自由表面が見つかると予想される領域全体にわたってメッシュが十分に密になっています. ただし, 3Dの場合, このタイプの解像度を常に使用できるとは限りません. 1つの方法は, アダプティブメッシュ細分化の機能を使用することです. この機能は, 選択した関数に応じて, より密なメッシュを自動的に作成します.
たとえば, 以下のアニメーションは, 速度の最大勾配の位置 (左) とフェーズフィールド関数の最大勾配 (右) に応じたメッシュのアダプテーションを示しています. プロットには, 空気相と水相の両方が表示されています. せん断速度に関するアダプティブメッシュ作成では, 空気相ではメッシュが細分化されますが, 水相ではそれほど細分化されないことに注意してください. この場合, 関心があるのは水相であるため, フェーズフィールド関数でスケーリングして, アダプティブメッシュ作成の誤差指数を変更する必要があります.
速度勾配を誤差指数として使用するアダプティブメッシュ細分化 (左) とフェーズフィールド勾配を誤差指数として使用するアダプティブメッシュ細分化 (右).
移動メッシュと自由表面
このブログでは, モデリングのための2つのフィールドベースの方法について説明します. 自由表面: フェーズフィールド法とレベルセット法. この2部構成のシリーズの2番目のブログでは, 移動メッシュを使用した自由表面のモデリングと, ここで紹介した場ベースの方法を比較します. お楽しみに!
更新: パート 2 が公開されました. こちらからお読みいただけます.
次のステップ
以下のボタンをクリックして, COMSOL Multiphysics のアドオンである CFD モジュールで利用できる流体の流れをシミュレートするための特殊な機能について詳しく学んでください.
その他の資料
- 自分で試してみましょう: アプリケーションギャラリから MPH ファイルをダウンロード
- レベルセット法とフェーズフィールド法のその他の実用的なアプリケーションについては, ブログを読んでください:
編集者注: このブログは, アプリケーションギャラリに追加されたサンプルモデルの MPH ファイルへのリンクを含めるために, 2018年5月25日に更新されました.






コメント (0)