
COMSOL Multiphysics® ソフトウェアは, 乱流問題を解くための様々な定式化を提供しています. L-VEL, 代数的 yPlus, Spalart-Allmaras, k-ε, k-ω, 低レイノルズ数 k-ε, SST, v2-f 乱流モデルです. これらの定式化は CFD モジュールで利用可能で, L-VEL, 代数的 yPlus, k-ε, 低レイノルズ数 k-ε モデルは伝熱モジュールでも利用可能です. このブログでは, これらの様々な乱流モデルを使用する理由, それらの選択方法, そしてそれらを効率的に使用する方法について説明します.
この記事は2013年に初版が公開されました. その後, COMSOL® ソフトウェアバージョン 5.3 以降の CFD モジュールで利用可能なすべての乱流モデルを網羅するように更新されました.
乱流モデリング入門
まず, 下図に示すように, 平板上の流体の流れを考えてみましょう. 一様な速度プロファイルが平板の前縁に衝突し, 層流境界層が形成され始めます. この領域の流れは非常に予測可能です. ある程度の距離を進むと, 境界層に小さなカオス的振動が生じ始め, 流れは乱流へと遷移し始め, 最終的には完全な乱流となります.
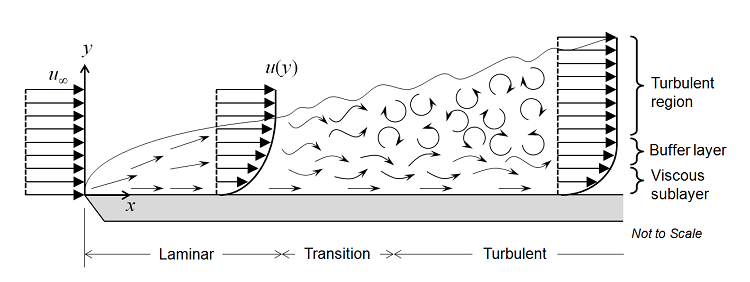
これら3つの領域間の遷移は, レイノルズ数, Re=\rho v L/\mu で定義できます. ここで, \rho は流体の密度, v は流速, L は代表長さ (この場合は前縁からの距離) です. また, \mu は流体の動粘性です. ここでは, 流体がニュートン流体であると仮定します. つまり, 粘性応力はせん断速度に正比例し, 動粘性が比例定数となります. これは, 空気や水など, 工学上重要なさまざまな流体に当てはまります. あるいは, ほぼ当てはまります. 密度は圧力に応じて変化しますが, ここでは流体が弱圧縮性であると仮定します. つまり, マッハ数 は約 0.3 未満です. COMSOL Multiphysics® の流体流れインターフェースの弱圧縮性流れオプションでは, 流れ場と圧力場に対する圧力波の影響は無視されます.
層流領域では, 速度場と圧力場を与える ナビエ・ストークス方程式 を解くことで, 流体の流れを完全に予測できます. まず, 速度場は時間とともに変化しないと仮定します. この例は, ブラシウス境界層 チュートリアルモデルに概説されています. 流れが乱流に移行し始めると, 入口流量が時間とともに変化しないにもかかわらず, 流れに振動が現れます. そうなると, 流れが時間に対して不変であると仮定することはできなくなります. この場合, 時間依存のナビエ・ストークス方程式を解く必要があり, 使用するメッシュは流れ内の最小の渦のサイズを解くのに十分な細かさでなければなりません. このような状況は, チュートリアルモデル 円柱を過ぎる流れ で実証されています. このモデルでは流れは非定常ですが, 層流であることに留意してください. 定常状態および時間依存の層流問題は, モジュールを必要とせず, COMSOL Multiphysics® だけで解くことができます.
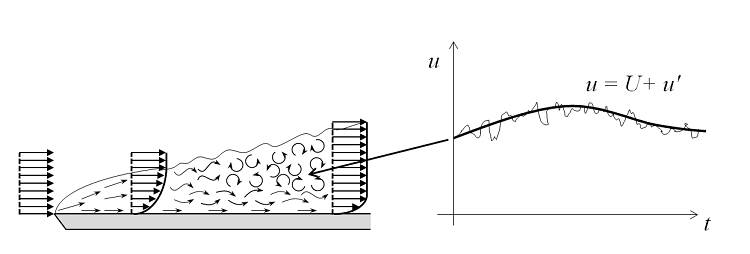
流量 (ひいてはレイノルズ数) が増加すると, 流れ場は小さな渦を呈し, 振動の空間的および時間的スケールが非常に小さくなるため, 少なくともほとんどの実用ケースでは, ナビエ・ストークス方程式を用いてこれらを解くことは計算上不可能になります. このような流れ場においては, レイノルズ平均ナビエ・ストークス (RANS) 定式化を使用することができます. これは, 流れ場 (u) の時間経過に伴って小さな局所振動 (u’) が含まれ, 時間平均 (U) として扱うことができるという観察に基づいています. 1方程式および2方程式モデルでは, 乱流運動エネルギー (k-ε および k-ω における k) などの乱流変数について, 追加の輸送方程式が導入されます.
代数モデルでは, 乱流強度を記述するために, 速度場 (場合によっては壁からの距離) に依存する代数方程式が導入されます. 乱流変数の推定値から, 流体の分子粘性に加算される渦粘性係数が計算されます. 小さな渦によって伝達されるはずの運動量は, 代わりに粘性輸送に変換されます. 通常, 固体壁に近い粘性層を除き, あらゆる場所で乱流散逸が粘性散逸よりも優勢です. このような場合, 低レイノルズ数モデルのように, 乱流モデルは乱流レベルを継続的に低減する必要があります. あるいは, 壁関数を用いて新たな境界条件を計算する必要があります.
低レイノルズ数モデル
“低レイノルズ数モデル” という用語は矛盾しているように聞こえます. なぜなら, 流れはレイノルズ数が十分に高い場合にのみ乱流となり得るからです. “低レイノルズ数” という表記は, 流れ全体ではなく, 粘性効果が支配的な壁近傍領域, つまり上図の粘性下層を指します. 低レイノルズ数モデルとは, 壁面からの距離がゼロに近づくにつれて, 様々な流量の限界挙動を正しく再現するモデルです. したがって, 低レイノルズ数モデルは, 例えば, y→0 のとき, k~y2 を予測する必要があります. 正しい限界挙動とは, 乱流モデルを使用して, 粘性下層と緩衝層を含む境界層全体をモデル化できることを意味します.
ほとんどの ω ベースモデルは, 構造上, 低レイノルズ数モデルです. しかし, 標準的な k-ε モデルやその他の一般的に用いられる k-ε モデルは, 低レイノルズ数モデルではありません. しかし, 一部のモデルは, 適切な限界挙動を与えるいわゆる減衰関数を補完することができます. これらは低レイノルズ数 k-ε モデルと呼ばれます.
低レイノルズ数モデルは, 境界層を非常に正確に記述することがよくあります. しかし, 壁面近傍の急激な勾配には非常に高いメッシュ解像度が必要であり, その結果, 高精度化には高い計算コストが伴います. そのため, 産業用途では, 壁面近傍の流れをモデル化する代替手法がよく用いられます.
壁関数
平坦な壁面近傍の乱流は4つの領域に分けられます. 壁面では流体の速度はゼロであり, その上の薄い層では, 流速は壁面からの距離に比例します. この領域は 粘性サブ層, または 層流サブ層 と呼ばれます. 壁からさらに離れた領域は 緩衝層 と呼ばれます. 緩衝領域では, 乱流応力が粘性応力よりも優勢になり始め, 最終的には流れが完全に乱流になり, 平均流速が壁までの距離の対数に比例する領域につながります. これは 対数法則領域 と呼ばれます. 壁からさらに離れると, 流れは 自由流領域 に移行します. 粘性層と緩衝層は非常に薄く, 緩衝層の端までの距離が \delta の場合, 対数則領域は壁から約 100\delta 離れたところまで広がります.
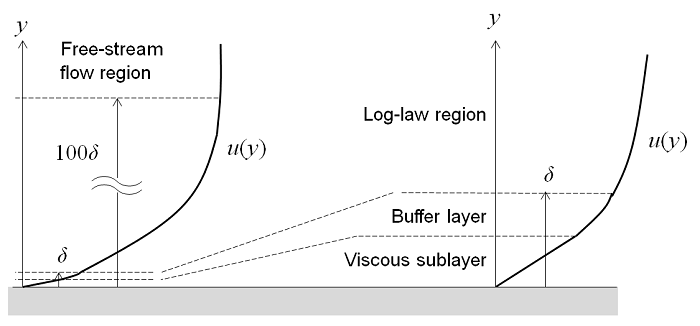
RANS モデルを用いて, これら4つの領域すべてにおける流れ場を計算することが可能です. しかし, バッファ層の厚さが非常に薄いため, この領域では近似値を用いる方が有利な場合があります. 壁関数はバッファ領域の流れ場を無視し, 壁面における非ゼロの流体速度を解析的に計算します. 壁関数定式化を用いることで, 粘性層内の流れに対して解析解を仮定し, 結果として得られるモデルの計算要件を大幅に低減できます. これは, 多くの実用的なエンジニアリングアプリケーションにおいて非常に有用なアプローチです.
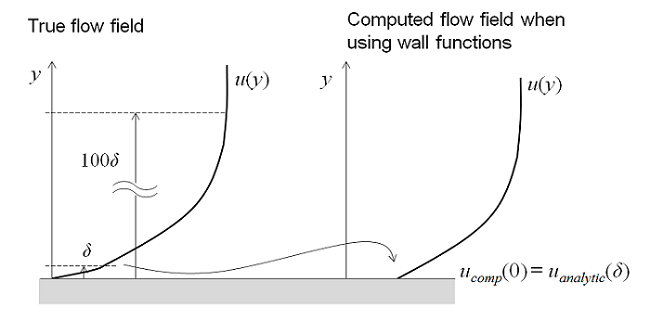
壁関数の定式化が提供する以上の精度が必要な場合は, 上記の低レイノルズ数モデルで説明したように, 流れ場全体を解く乱流モデルを検討する必要があります. 例えば, 物体の 揚力と抗力 を計算したり, 流体と壁の間の熱伝達を計算したりすることができます.
自動壁処理
COMSOL Multiphysics® バージョン 5.3 の新機能である 自動壁処理機能 は, 壁関数と低レイノルズ数モデルの両方の利点を兼ね備えています. 自動壁面処理は, モデルで利用可能なメッシュに合わせて定式化を適応させることで, 堅牢性と精度の両方を実現します. 例えば, 粗い境界層メッシュの場合, この機能はロバストな壁関数定式化を利用します. 一方, 密な境界層メッシュの場合, 自動壁処理機能により低レイノルズ数定式化が使用され, 速度プロファイルが壁まで完全に解かれます.
低レイノルズ数定式化から壁関数定式化への移行はスムーズです. ソフトウェアは境界要素内で2つの定式化を統合します. 次に, 境界要素のグリッドポイントの壁距離 (リフトオフによって与えられる粘性単位) を計算します. 統合された定式化は境界条件に使用されます.
COMSOL Multiphysics® の k-ε モデルを除くすべての乱流モデルは, 自動壁処理をサポートしています. つまり, 低レイノルズ数モデルは産業用途に使用でき, 低レイノルズ数モデリング機能はメッシュが十分に細かい場合にのみ呼び出されます.
様々な乱流モデルについて
8つの RANS 乱流モデルは, 壁面近傍の流れをモデル化する方法, 解く追加変数の数, そしてそれらの変数が表す内容が異なります. これらのモデルはすべて, ナビエ・ストークス方程式に乱流渦粘性項を追加しますが, その計算方法は異なります.
L-VEL と yPlus
L-VEL および代数的 yPlus 乱流モデルは, 局所的な流体速度と最も近い壁までの距離のみに基づく代数式を用いて渦粘性を計算します. これらのモデルは追加の輸送方程式を解きません. これらのモデルはあらゆる場所の流れを解析し, 8つの乱流モデルの中で最も堅牢で計算負荷が低いモデルです. 一般的に精度は最も低いモデルですが, 特に電子機器冷却アプリケーションにおいて, 内部流れに対して良好な近似値を提供します.
Spalart-Allmaras
Spalart-Allmaras モデルは, 減衰のない動渦粘性に1つの追加変数を追加します. これは低レイノルズ数モデルであり, 流れ場全体を固体壁まで解像できます. このモデルはもともと空気力学アプリケーション用に開発されたもので, 比較的堅牢で, 解像度要件が中程度であるという利点があります. 経験上, このモデルはせん断流, 剥離流, または減衰乱流を示す場を正確に計算できないことが分かっています. その利点は, 非常に安定しており, 良好な収束性を示すことです.
k-ε
k-ε モデルは, 乱流運動エネルギー k と, 乱流運動エネルギーの散逸率 ε (イプシロン) という2つの変数を解きます. このモデルでは壁関数が使用されるため, バッファ領域内の流れはシミュレートされません. k-ε モデルは, 良好な収束速度と比較的低いメモリ要件から, これまで産業用途で非常に人気がありました. 逆圧力勾配, 流れの強い曲率, または噴流を示す流れ場をあまり正確に計算できません. 複雑な形状周辺の外部流れの問題には優れた性能を発揮します. 例えば, k-ε モデルは, 鈍角物体周辺の気流 を解くのに使用できます.
以下に挙げる乱流モデルはすべて k-ε モデルよりも非線形性が高く, 適切な初期推定値を与えなければ収束が困難になる場合があります. k-ε モデルは適切な初期推定値を与えるために使用できます. k-ε モデルを使用してモデルを解き, 新しい乱流インターフェースの生成 機能を使用するだけです. この機能の詳細については, ラーニングセンターの記事 の2つ目のビデオの最後の部分をご覧ください.
k-ω
k-ω モデルは k-ε モデルに似ていますが, 運動エネルギーの消散率である ω (オメガ) を解きます. 低レイノルズ数モデルですが, 壁関数と組み合わせて使用することもできます. k-ε モデルよりも非線形性が高く, 収束が困難で, 解の初期推定値に非常に敏感です. k-ω モデルは, 内部流れ, 強い曲率を示す流れ, 剥離流れ, ジェットなど, k-ε モデルが正確ではない多くのケースで有用です. 内部流れの良い例としては, 曲がり管の流れ が挙げられます.
低レイノルズ数 k-ε
低レイノルズ数 k-ε モデルは k-ε モデルに似ていますが, 壁関数を必要とせず, あらゆる流れを解くことができます. これは k-ε モデルの論理的な拡張であり, 多くの利点を共有していますが, 一般的にはより高密度のメッシュを必要とします. これは壁面だけでなく, 低レイノルズ数特性が作用して乱流を減衰させるあらゆる箇所で発生します. 低レイノルズ数 k-ε モデルを解くための適切な初期条件を最初に計算するために, k-ε モデルを使用することが有用な場合があります. 別の方法としては, 自動壁面処理を使用し, 粗い境界層メッシュから始めて壁関数を取得し, 次に対象となる壁面で境界層を細分化して低レイノルズ数モデルを取得する方法があります.
低レイノルズ数 k-ε モデルは, 揚力と抗力を計算でき, 熱流束を k-ε モデルと比較してより高い精度でモデル化できます. また, 多くのケースにおいて剥離と再付着を非常に正確に予測できることも示されています.
SST
SST モデルは, 自由流における k-ε モデルと壁面近傍における k-ω モデルを組み合わせたものです. これは低レイノルズ数モデルであり, 産業用途では定番のモデルです. k-ω モデルや低レイノルズ数 k-ε モデルと同様の解像度要件を備えていますが, その定式化により, 純粋な k-ω モデルや k-ε モデルに見られるいくつかの弱点が解消されています. チュートリアルのモデル例では, SST モデルを用いて NACA 0012 Airfoil 上の流れを解析します. 結果は実験データとよく一致しています.
v2-f
壁面境界付近では, 通常, 壁面に垂直な方向と比較して, 壁面に平行な方向の速度変動ははるかに大きくなります. この速度変動は異方性があると言われています. 壁面から離れるにつれて, 変動はすべての方向で同じ大きさになります. 速度変動は等方性になります.
v2-f 乱流モデルは, 乱流運動エネルギー (k) と散逸率 (ε) の2つの方程式に加えて, 2つの新しい方程式を用いて, 乱流境界層における乱流強度の異方性を記述します. 最初の方程式は, 流線に垂直な方向の乱流速度変動の輸送を記述します. 2番目の方程式は, 法線方向と平行方向間の乱流運動エネルギーの再分配における壁面誘起減衰などの非局所的効果を考慮します.
このモデルは, 曲面上の密閉流れ, 例えば サイクロンのモデル化 に用いることができます.
CFD 問題におけるメッシュ分割の考慮事項
層流問題であれ乱流問題であれ, あらゆる種類の流体流れ問題を解くには, 膨大な計算量が必要です. 比較的細かいメッシュが必要であり, 解くべき変数も多数あります. 理想的には, このような問題を解くには数ギガバイトの RAM を搭載した非常に高速なコンピュータが必要ですが, 大規模な3Dモデルではシミュレーションに数時間から数日かかることがあります. そのため, 流れの細部をすべて捉えつつ, 可能な限りシンプルなメッシュを使用することが重要です.
このブログの冒頭の図を見ると, 平板 (およびほとんどの流れ問題) の場合, 速度場は壁面の接線方向には非常に緩やかに変化しますが, 法線方向には非常に急速に変化することが分かります. 特にバッファ層領域を考慮すると顕著です. この観察結果から, 境界層メッシュを使用する理由が分かります. 境界層メッシュ (物理ベースメッシュを使用する場合, 壁面のデフォルトのメッシュタイプ) は, 2Dでは薄い長方形, 3Dでは三角柱を壁面に挿入します. これらの高アスペクト比要素は, 境界に垂直な方向の流速の変化をうまく計算すると同時に, 境界の接線方向の計算点数を削減します.
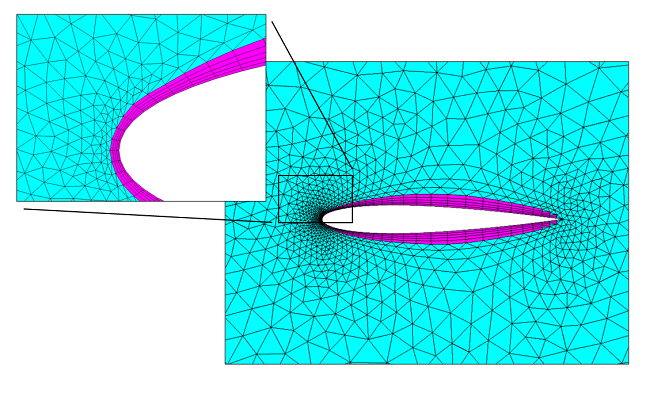
翼型周囲の境界層メッシュ (マゼンタ) と, 2Dメッシュの周囲の三角形メッシュ (シアン).

鈍体周囲の境界層メッシュ (マゼンタ) と, 3Dボリュームメッシュの周囲の四面体メッシュ (シアン).
乱流モデルの結果評価
これらの乱流モデルのいずれかを使用して流れのシミュレーションを実行したら, 解の正確性を検証する必要があります. もちろん, 他の有限要素モデルと同様に, メッシュを徐々に細かくして実行し, メッシュの細分化によって解がどのように変化するかを観察するだけで済みます. 解が許容範囲内に変化しなくなったら, シミュレーションはメッシュに関して収束したと見なすことができます. ただし, 乱流をモデル化する際に確認する必要がある追加の値があります.
壁関数の定式化を使用する場合は, 壁解像度粘性単位 を確認する必要があります (このプロットはデフォルトで生成されます). この値は, 計算領域が境界層のどのくらい深くまで始まるかを示しており, あまり大きくしすぎないようにしてください. 壁解像度が数百を超える領域がある場合は, 壁法線方向にメッシュを細分化することを検討する必要があります. 壁関数を使用する際に確認すべき2つ目の変数は, 壁面リフトオフ (長さ単位) です. この変数は粘性層の想定厚さに関連し, ジオメトリの周囲の寸法に比べて小さくする必要があります. 小さくない場合は, これらの領域でもメッシュを細分化する必要があります.
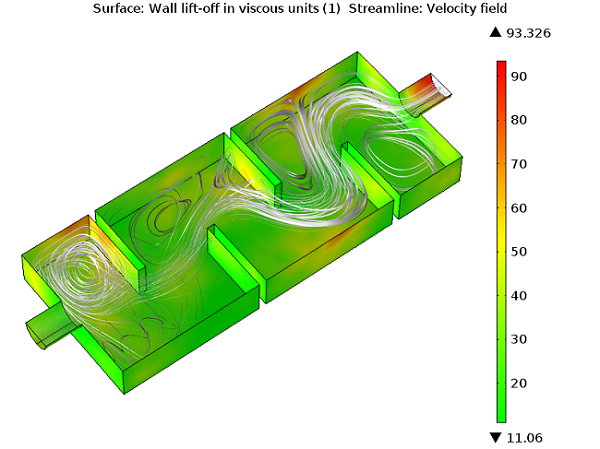
粘性ユニットにおける壁面リフトオフの最大値は 100 未満であるため, 境界層メッシュを細分化する必要はありません.
低レイノルズ数壁処理を用いてモデルを解く場合は, セル中心までの無次元距離 (これもデフォルトで生成されます) を確認してください. この値は, 代数モデルの場合はどこでも 1 のオーダー, すべての2方程式モデルと v2-f モデルの場合は 0.5 未満である必要があります. そうでない場合は, これらの領域のメッシュを細分化してください.
まとめ
このブログでは, COMSOL Multiphysics® で利用可能な様々な乱流モデルについて説明し, それぞれのモデルをいつ, なぜ使用すべきかについて重点的に説明しました. COMSOL® ソフトウェアの真の強みは, 流体シミュレーションを他の物理現象と組み合わせる際に発揮されます. 例えば, 強風下におけるソーラーパネルの応力計算, 熱交換器における強制対流モデリング, ミキサーにおける物質移動 などです.
COMSOL® ソフトウェアを CFD およびマルチフィジックスシミュレーションにご利用いただくことにご興味をお持ちの場合, またはここで取り上げられていないご質問がある場合は, お気軽にお問い合わせください.






コメント (0)