
有限要素モデルでは, さまざまな状況で数値積分とガウス点の概念に遭遇することがあります. このブログでは, 数値積分が使用される場所と理由について説明します. また, COMSOL Multiphysics® ソフトウェアで数値積分スキームを検査および変更できる可能性についても説明します. 最後に, ガウス点の自由度の使用について説明します.
目次
数値積分とは?
一般領域で非自明な関数の積分を計算する場合, 数値法に頼る必要があります. 数値積分は, 数値求積法 とも呼ばれます. 積分を合計に置き換え, 被積分関数をいくつかの離散点でサンプリングするという考え方です. これは次のように記述できます
ここで, xi は積分点の位置, wi は対応する重み係数です. 積分点はしばしば ガウス点 と呼ばれますが, 厳密に言えば, この命名法は ガウス求積法 法によって定義された積分点にのみ当てはまります. COMSOL Multiphysics では, 1Dでの積分には真のガウス求積法, 2Dでは四辺形要素, 3Dでは六面体要素が使用されます. その他の要素ジオメトリには, 他の同様のスキームが使用されます.
ガウス積分法
ガウス積分法アルゴリズムでは, 積分点の位置とその重みは, できるだけ高い次数の多項式を正確に積分できるように選択されます. 次数 N の多項式には N+1 個の係数が含まれ, M 点のガウス点規則には 2M 個のパラメータ (位置 + 重み) が含まれるため, 正確に積分できる多項式の最高次数は N = 2M – 1 です.
ガウス積分法は, 特定の次数の多項式で十分に近似できるフィールドを積分するのに非常に効率的です. 1Dのガウス積分法の1次数の積分点と重みを次の表に示します. 積分は, 正規化された区間 [-1,1] で行われます.
| 順序 (M) | 精度 (N) | 位置 (xi) | 重量 (wi) |
|---|---|---|---|
| 1 | 1 | 0 | 2 |
| 2 | 3 | ±0.577 | 1 |
| 3 | 5 | 0, ±0.775 | 0.889 (= 8/9), 0.556 (= 5/9) |
| 4 | 7 | ±0.340, ±0.861 | 0.652, 0.348 |
| 5 | 9 | 0, ±0.538, ±0.906 | 0.569, 0.479, 0.237 |
COMSOL Multiphysics では, 積分次数は正確に積分できる多項式の次数で指定されます. 偶数のみが使用されます. 真のガウス点積分の場合, 精度は上記のように常に奇数乗です. ソフトウェアによって “4” として指定された積分次数は, ガウス求積法が使用される要素形状では実際には精度 5 になります.
ガウス積分法の例
ガウス積分法の例として, 関数を考えてみましょう
-1 ≤ x ≤ 1, -1 ≤ y ≤ 1 の正方形上では, この関数の積分は 1 です. 下の図からわかるように, この関数はドメイン上でかなり複雑な分布をしています.
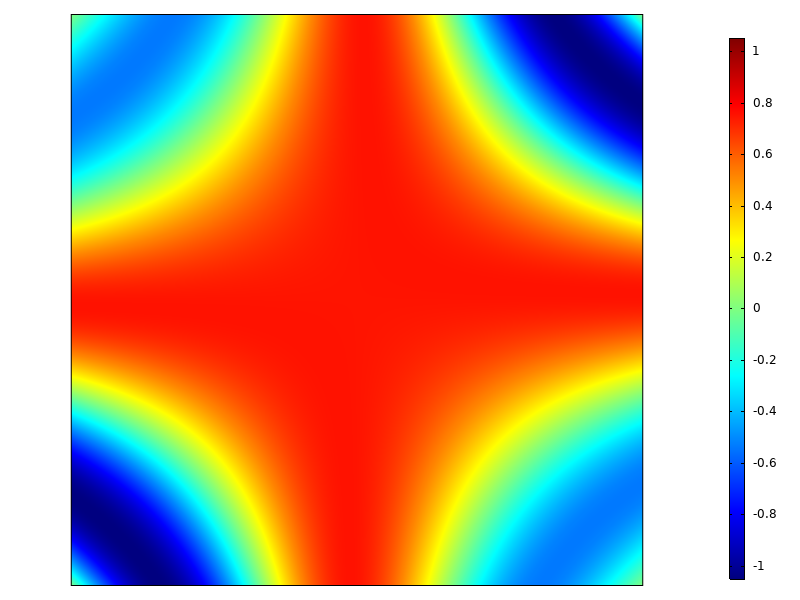
積分する関数.
下の表には, さまざまなガウス積分次数の結果が示されています. 関数が特定の次数の多項式で適切に近似できるようになると, 積分の値は急速に収束します.
| 積分点 | 精度 | 積分次数 | 値 | コメント |
|---|---|---|---|---|
| 1 | 1 | 0 (または 1) | 2.9958 | 重心の値のみを使用すると, 積分が明らかに過大評価されます |
| 2×2 | 3 | 2 (または 3) | 0 | 2×2 ルールでは, ガウス点は \pm \frac{1}{\sqrt{3}} にあります, 余弦関数は 0 です (不運!) |
| 3×3 | 5 | 4 (または 5) | 1.1519 | |
| 4×4 | 7 | 6 (または 7) | 0.9887 | |
| 5×5 | 9 | 8 (または 9) | 1.0005 | |
| 6×6 | 11 | 10 (または 11) | 1.0000 | |
| 7×7 | 13 | 12 (または 13) | 1.0000 | |
| 8×8 | 15 | 14 (または 15) | 1.0000 |
ただし, 多項式に対するガウス積分法の最適な動作には欠点があります. この方法は, 非常に不連続な関数を積分するのにはあまり適していません. y < -2x – 1 のときに f(x,y) = 1 に等しく, それ以外の場合は 0 となる関数を, 上記と同じ正方形上で積分するとします. 関数は正方形の4分の1で値 1 を持ち, 正方形の面積は 4 であるため, 正確な積分は 1 に評価されるはずであることがすぐにわかります. 結果を下の表に示します.
| 積分点 | 値 | コメント |
|---|---|---|
| 1 | 0 | (0,0) の1つの点のみ, 関数は 0 と評価されます |
| 2×2 | 1 | 4つの点のうち1つは 1 と評価され, その重みは 1 です |
| 3×3 | 0.8025 | 2つの点は 1 と評価され, その重みは \frac{25}{81}, \frac{40}{81} |
| 4×4 | 1.2269 | 5つの点を評価すると 1 |
| 5×5 | 1.0325 | |
| 6×6 | 1.0918 | |
| 7×7 | 0.9892 | |
| 8×8 | 0.9961 |

4×4 積分点の場合. オレンジ色の表面は関数の値が 1 になる部分で, 緑色のガウス点は積分値に寄与する部分です.
表からわかるように, この不連続関数の正確な積分を計算するにはかなりの労力が必要です. まったくの偶然ですが, 2×2 積分方式では正確な答えが得られますが, 収束は単調とはほど遠いです.
なぜこれが重要なのでしょうか. 有限要素解析 では, 急激な局所勾配を示す場に遭遇することがあります. いくつかの例としては, 相転移や固体力学における塑性の開始時の問題があります. このようなジャンプを含む要素に対して計算される積分には, 重大な離散化エラーが発生する可能性があります. また, 解の収束性が損なわれる可能性があります. 解の小さな変化は, 個々のガウス点の状態が変化すると, 計算された残差を大幅に変える可能性があります.
このような場合, 場を離散化するために使用される形状関数のデフォルトよりも低い多項式次数を選択する方がよい場合があります. 解像度が低い場合は, より高密度のメッシュを使用することで補正できます. その結果, 必然的なジャンプは, 積分点の少ない小さな要素に限定されます.
また, ポスト処理中に不連続関数の積分を計算する場合, 数値積分の潜在的に遅い収束を念頭に置くことが重要です.
弱寄与の積分
各有限要素内には, 剛性行列, 質量行列, 荷重ベクトル, 残差などを形成するために積分する必要があるさまざまな式があります. 固体力学を例にとると, 標準的な弱定式化 (または変分) は, 仮想仕事の原理 に対応します. 仮想ひずみの変化に作用する内部応力によって行われる仮想仕事は, 対応する変位の仮想変化に作用する外部力によって行われる仮想仕事に等しくなります.
ここで, チルダ (~) は仮想変化を表します. COMSOL Multiphysics の式では, これは test() 演算子で表されます. 体積力 f と境界牽引力 t はここに含まれていますが, 他の種類の寄与もある可能性があります. 左側は剛性行列に寄与し, 右側は荷重ベクトルに寄与します (力が変位に依存しないと仮定した場合).
COMSOL Multiphysics で有限要素実装の定式化を検査するには, 方程式ビュー を有効にする必要があります.
方程式ビュー をオンにする
固体力学 インターフェースの材料モデル (線形弾性材料 など) の 方程式ビュー を見ると, 弱形式 というセクションがあります. そこでは, たとえば, 剛性行列のようなさまざまな行列を形成するために使用される式を確認できます.
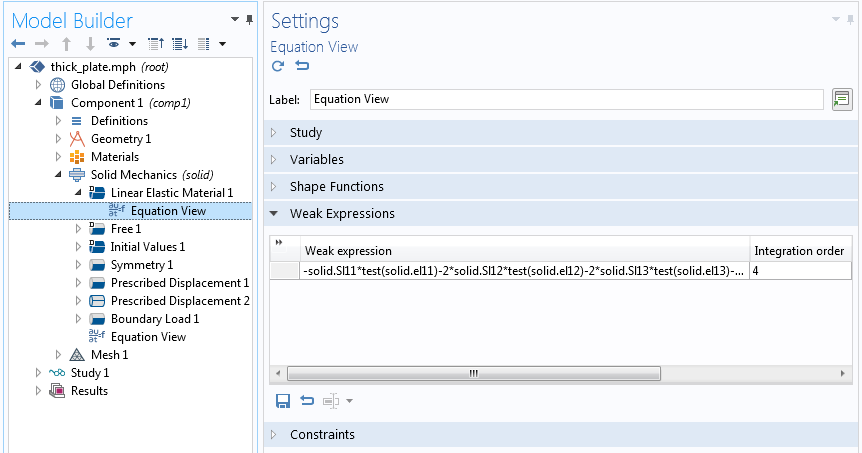
定常ケースの 固体力学 インターフェースで 線形弾性材料 の弱形式をチェックします.
上の図では, 積分次数のテキストフィールドが表示されています. この場合は値が 4 です. COMSOL Multiphysics で積分次数を表す数値は, 正確に積分できる多項式の最高次数です. デフォルトの積分次数は, 場 (この場合は変位) を表すために使用される形状関数の次数に基づいています. ここでは, デフォルトの形状関数次数 (2次) が使用されているため, 応力とひずみは基本的に要素全体で線形に変化します. 応力とひずみの変化の積は2次であるため, 次数 4 は必要以上に大きい可能性があります. この値が選択された理由については, 以下で説明します.
2番目の例として, 固体力学 の 境界荷重 を調べてみましょう.
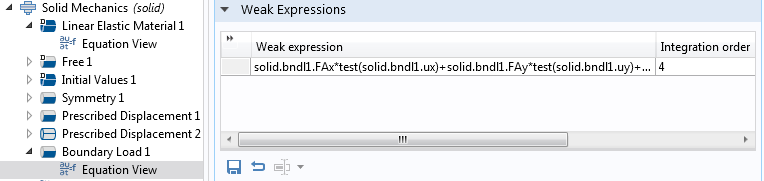
境界荷重 の弱形式
ここでも, 積分次数は 4 です. 変位形状関数は2次多項式であるため, 牽引力が2次変化を超えない荷重寄与を正確に積分できるはずです. 牽引力と変位の変化の積は4次です.
弱形式に関する微妙な点
上記の説明は, 要素が理想的な形状 (曲線境界がないなど) である場合にのみ厳密に当てはまります. 理論を詳しく調べると, 積分には実際の要素形状と公称要素形状間の変換から生じるローカルスケール係数 (ヤコビアン) も含まれています. たとえば, 2D四辺形要素に対して積分を実行する場合, 数値評価は理想的な正方形 -1 ≤ ξ ≤ 1, -1 ≤ η ≤ 1 に対して実行されます.
ヤコビアンは一般に有理関数 (分子と分母の両方で多項式) になるため, このタイプの数値積分法では正確に積分できない可能性があります. このため, 選択した積分次数にいくらか余裕を持たせることが賢明です. ちなみに, ヤコビアン効果は, ひどく歪んだ要素が理想的な形状の要素よりもパフォーマンスが低下する理由の1つです. この COMSOL Multiphysics でのメッシュの検査に関するブログ には, メッシュの品質に関する詳細情報が記載されています.
要素の形状関数が “2次” と呼ばれていても, (場合によっては) 高次の項が含まれていることがあります. ユーザーインターフェースに表示される形状関数の次数は, 形状関数内の最も完全な多項式を示しています. 多項式に高次の項が存在する可能性があるという事実は, 一見必要と思われるものよりも正確な積分規則を使用するもう1つの理由です.
特定の寄与に対して 方程式ビュー で予想よりも高い積分次数が表示されるもう1つの理由は, 剛性行列の対称性を確保する必要がある場合があることです.
積分次数の変更
方程式ビュー からテキストフィールドを編集することで, 任意の弱形式の積分次数を変更できます. これを行う主な理由は2つあります.
1つ目はより明白な理由です. 精度を向上させたい場合です. 要素のサイズと比較して変化が速い負荷 (一般的な意味では, 力, 熱流束, 電流など) があるとします. 数値積分の順序を上げると, ドメインへの合計力または流束の精度が向上します. ただし, 境界条件が適用される場所に近いローカルな解は, 要素の形状関数が表すことができるものよりも優れていることは決してないため, 依然として適切ではありません.
ただし, もう1つ興味深いケースがあります. それは, 縮小積分 です. これは, 何らかの理由で, 積分次数が正式に必要とされるものよりも低いことを意味します. その理由の1つは, 計算を高速化することです. 有限要素問題を解く場合, CPU 時間の大部分は, 要素行列の形成 (アセンブリ) と大規模な線形方程式の系の求解という2つのタスクに費やされます. 方程式の求解に費やされる時間は, モデルサイズよりも速く増加し, 多くの場合, 要素数の2乗にほぼ比例します. アセンブリに費やされる時間は, モデルサイズに正比例します (実際には, 要素数に要素あたりの積分点の数を掛けた値です). 非常に大規模なモデルでは, 方程式の求解が常に優先されますが, 各積分点で大量の計算が行われる中規模の非線形モデルでは, 縮小積分の使用を検討する価値がある場合があります.
縮小積分は, いくつかの要素定式化でしばしば ロッキング と呼ばれる現象で現れる人工的な剛性を除去するために使用されることもある数値デバイスでもあります. 縮小積分がこの目的で使用される1つの例は, 2D軸対称の シェル インターフェースにあります. 仮想作業方程式では, 一部の項は2次で積分され, 他の項は4次で積分されます. すべての場所で完全積分を使用すると, シェルの厚さが小さくなると, 要素は実際には非常に硬くなります. 縮小積分を使用することで, ひずみエネルギーの問題のある項の一部が意図的に失われます.

軸対称 シェル インターフェースの仮想作業寄与.
編集者注: 次のセクションは, COMSOL Multiphysics バージョン 6.0 で利用可能な新機能に関する情報を含めるために, 2023年5月4日に追加されました.
組込みの縮小積分
一部の 構造力学 インターフェースには, 特定の材料モデルの設定から直接縮小積分を選択するオプションが含まれています.
線形弾性材料 の設定ウィンドウの 求積設定 セクション.
方程式ビュー で積分次数を編集する場合と比べて, この方法にはいくつかの利点があります:
- 変更は1か所で実行でき, 可能なサブノードに自動的に反映されます.
- 適切な縮小積分スキームについて心配する必要はありません.
- 一部の要素形状関数では, 積分次数を下げると剛性行列が特異になります. これは, 組込みの アワーグラス安定化 機能によって調整されます.
- 塑性などの一部の材料モデルでは, 積分点にローカル状態が保存されます. これは, 積分ルールと自動的に同期されます.
積分カップリング演算子
モデルビルダーの 定義 で, 積分演算子 を作成できます. このような演算子は, 問題の定式化の一部であるグローバル変数を定義するために使用できますが, 結果の評価中に式で明示的に使用することもできます.
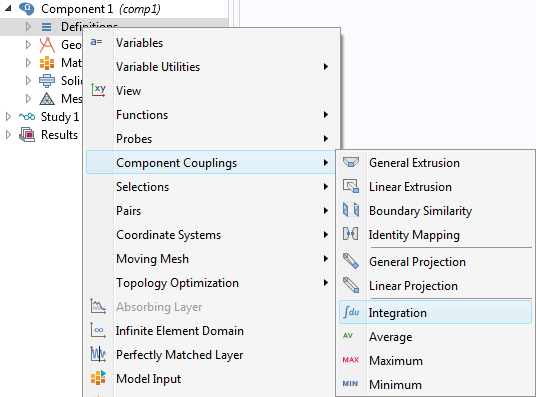
積分演算子の追加.
積分演算子を追加するときは, 主に3つの選択を行う必要があります:
- 積分を行う領域, 境界, またはエッジ.
- 積分次数 — これによって, 精度と速度をトレードオフするオプションも提供されます. 実際の積分対象は, 指定した式だけでなく, 理想要素形状から実要素形状への変換のヤコビアンも乗算されることに注意してください.
- 座標系 — 移動メッシュ, 変形ジオメトリ, 構造力学における幾何学的非線形性など, 異なる座標系が存在する場合にのみ重要になります. 簡単に言うと, 積分は変形ジオメトリに対して行うべきでしょうか, それとも変形されていないジオメトリに対して行うべきでしょうか?
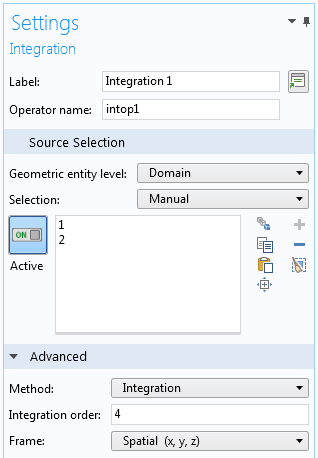
積分演算子の設定.
ポスト処理中の積分
ポスト処理中に積分を計算する場合, 積分演算子を使用する (上記参照) か, 導出値 の下に 積分 ノードを追加するという2つのオプションがあります. 選択は大部分が任意です. ただし, 積分 ノードでは, 積分の座標系を明示的に選択することはできません. これは, データセット ノードの座標系選択から推測されます.
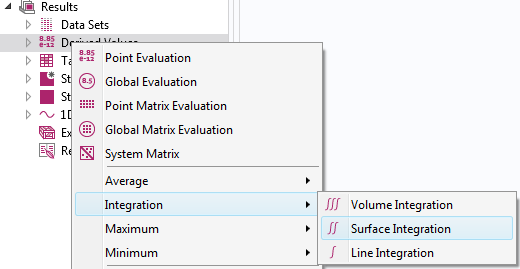
結果評価中に統合用のノードを追加します.
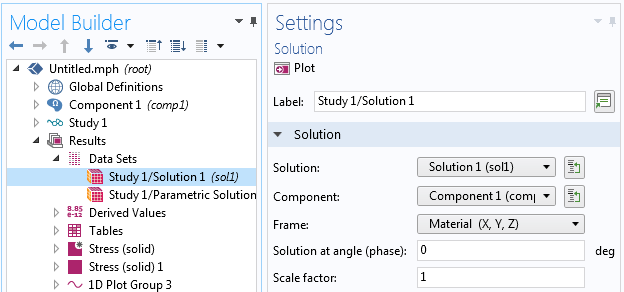
結果解釈用の座標系を選択できるデータセットの設定.
座標系の選択が重要な場合は, 微妙なエラーが発生するリスクを最小限に抑えるために, 積分演算子に頼る必要があるでしょう. 問題を解いた後に積分演算子を追加する場合は, 新しい演算子にアクセスできるようになる前に, 解の更新 を実行する必要があります.
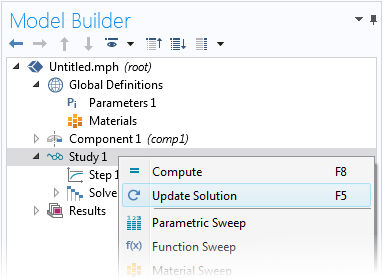
解の更新.
十分に高い積分次数を選択することを忘れないでください. 特に, 積分する式が強い非線形または不連続である場合は注意してください. 不連続式の一般的な特殊なケースは, ブール式です. たとえば, 熱伝達解析後に温度が特定の値を超える体積を計算する場合は, T>1066[K] のような積分関数を使用できます. この式は, 条件が満たされる場所では 1 に評価され, それ以外の場所では 0 に評価されるため, 積分すると条件が満たされる体積が得られます. ただし, 2つの値の境界は, 一般に要素を切断します.
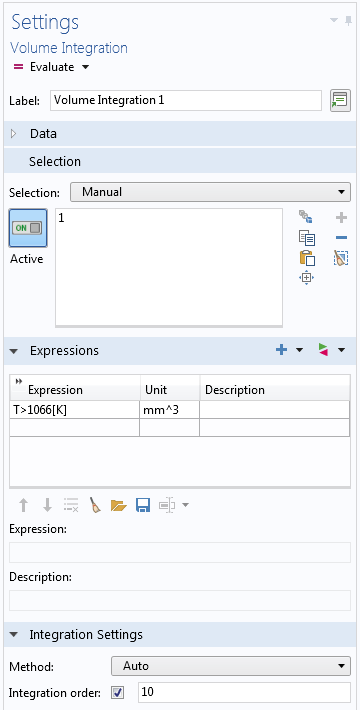
積分精度を高めたブール式の積分.
ガウス点形状関数
マルチフィジックスモデルを拡張する場合, ユーザー定義の自由度 (従属変数) を追加する必要があることがあります. その場合, それらを表すために使用する形状関数のタイプを選択する必要があります. オプションの1つは ガウス点データ です. 他のすべてのオプションは, 要素全体に連続的に分布し, 隣接する要素間で連続しているかどうかわからないさまざまなタイプの場を提供します. ガウス点データ タイプの “形状関数” は根本的に異なります. 各ガウス点に値を格納するだけで, 要素内の他の場所の値とは関係がありません.
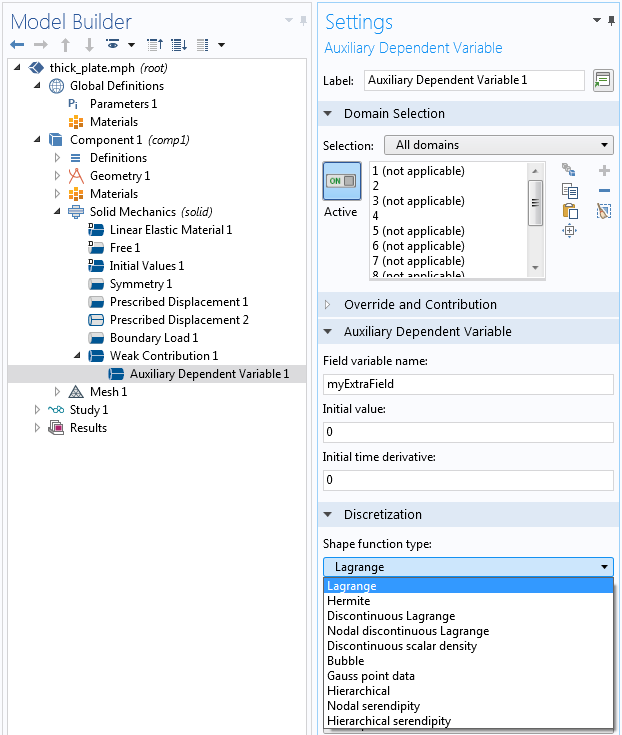
ユーザー定義の従属変数の形状関数のタイプを選択します.
ガウス点データ タイプは, ローカル状態を保存する場合に便利です. この状況は, たとえば, “メモリ” を必要とする履歴依存の非線形構成モデルで発生します. 構成モデルは主に剛性行列と残差を計算するときにアクセスされるため, 解法中に実際に評価される要素内の場所は積分点のみです. したがって, このタイプのデータをまさにそこに保存することは理にかなっています.
ガウス点データが内部的に使用される例の1つは, 構造力学における塑性やクリープなどの材料モデルにおける非弾性ひずみの保存です.
ガウス点データを保存することを決定したら, 要素次数 を選択する必要があります. ガウス点データの場合, これは前述の積分次数と同じです. ガウス点データの保存にかかるコスト (メモリと CPU 時間の観点から) は, 1Dでは選択した次数に比例し, 2Dではその2乗, 3Dでは3乗になります.
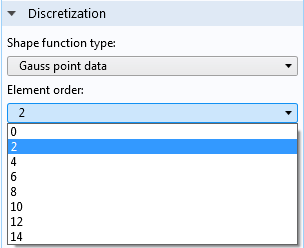
積分点パターンの選択.
組込みのフィジックスインターフェイスと一緒に使用するガウス点変数を追加する場合は, 通常, 関連する弱形式の計算に使用した積分次数と同じ積分次数を選択する必要があります. 不一致があると, 要素内の異なる場所間で値を転送する必要があり, 精度とパフォーマンスが低下します.
gpeval 演算子
組込みまたは自分で定義したガウス点に変数が格納されている場合, 要素上でそれらを補間する必要がある状況があります. これは, ポスト処理中に特に重要です. デフォルトでは, 要素内の別の場所で評価されたときに, ガウス点変数の値は最も近いガウス点から選択されます. gpeval() 演算子を使用すると, 離散ガウス点データを連続フィールドにマッピングできます. 最も単純な形では, 演算子は gpeval(gporder, expression) として参照されます. たとえば, gpeval(4,solid.epe) です. 詳細については, COMSOL Multiphysics ユーザーガイド を参照してください.
例として, 次の例を考えてみましょう. x 座標 (0 から 3 の範囲) は, 小さな3要素モデルにガウス点データとして保存されます. これは, 次に示すように, 補助従属変数を追加することで行われます.
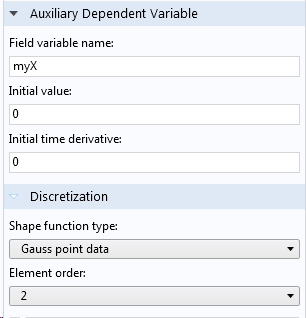
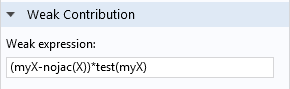
x 座標をガウス点データとして保存します.
弱寄与 (myX-nojac(X))*test(myX) は単に “変数 myX を X の現在の値に設定する” と述べています. nojac() 演算子は, myX と X の間に双方向の結合が生じないようにするための安全策として追加されています. 従属変数に値を割り当てるだけの場合は, この演算子を使用することをお勧めします.
ガウス点変数 myX を表面プロットとしてプロットすると (要素間の平均化を行わない), 結果は不連続になります. 各要素内で, ガウス点変数は最も近いコーナーに移動され, 要素上で補間されます. 代わりに, 式 gpeval(2,myX) をプロットすると, 正確な x 座標分布が取得されます.
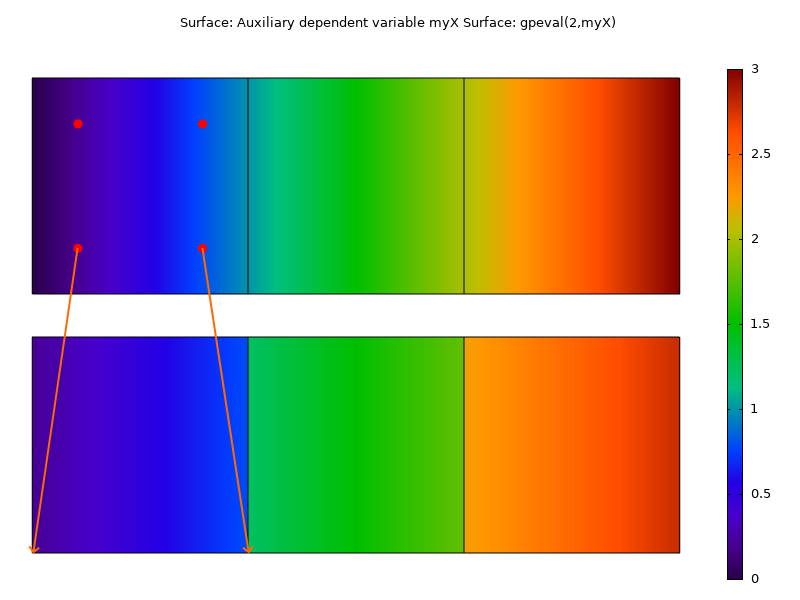
ガウス点変数 (下) と外挿されたガウス点変数 (上) をプロットします. 矢印は, 結果評価中にガウス点データがデフォルトでコーナーに移動される様子を示しています.
次のステップ
以下のボタンをクリックして, COMSOL® ソフトウェアで利用できる機能の詳細をご覧ください:






コメント (0)