
溶接は, 金属構造を接合するための最も一般的な手法の1つです. これは, いくつか例を挙げると, 建設, 石油, ガス産業, 造船などの分野で使用される確立されたソリューションです. 溶接は, 接合された部品の機械的, 化学的, および冶金学的特性を変更する複雑な現象です. このブログでは, 有限要素モデルで溶接を表現するためのさまざまな手法と, 溶接の応力を評価して疲労寿命を推定する方法に焦点を当てます.
溶接プロセスの概要
溶接は, 高温を使用して母材を溶かすことにより, 2つの部品間に永続的な結合を作成する一連のプロセスです. 燃焼, 電流, 電子ビーム, 摩擦, 超音波などのさまざまなエネルギー源を使用して, 溶接プロセスに必要な温度を実現できます. 溶接は金属や熱可塑性プラスチックにも適用できますが, ここでは主に金属の溶接に焦点を当てます.
溶接プロセスは材料の変化を引き起こし, 溶接部の応力の評価を複雑な作業にします. これらの課題には次のものがあります:
- 化学組成の変化
- 溶接プール内での合金の直接混合または高温拡散により合金成分の濃度が変化するため, 母材およびフィラー合金 (存在する場合) は, プロセス中に化学組成を変化させる可能性があります.
- 冶金構造の変化
- 溶接プロセス中の高温は, 溶接プールに隣接する領域の微細構造を変化させる可能性があります. 同じ化学組成の合金は, 高温からの冷却中に続く熱プロファイルのために, 異なる微細構造を示す場合があります. この変更により, 降伏応力, 延性, 硬度などの材料の機械的特性も変更されます. 金属プロセスモジュールは, 金属合金におけるこれらの影響を解析するために使用できます.
- 熱機械的効果
- プロセス中の温度差と合金の熱膨張により, 接合部に熱応力が発生します. 高温でのほとんどの合金の降伏応力の減少により, この熱応力は母材または溶融ゾーンの降伏応力に達する可能性が非常に高く, 接合部の永久的な反りとマイクロクラックを引き起こし, 疲労寿命に影響を与えます. プロセス中に発生する塑性ひずみは, 接合部の疲労寿命にも影響を与える残留応力を誘発します.
- 幾何学的変化
- 使用する熱源の一部の脈動性またはプロセス自体の変動性により幾何学的な変化が発生し, 理想的なプロファイルとは異なる溶接形状が発生する可能性があります. この変動は, 追加の応力集中を引き起こす可能性があります.
COMSOL Multiphysics® ソフトウェアで完全な溶接プロセスをシミュレートすることは可能ですが, レーザービーム溶接に関するこのブログで説明されているように, またはレーザービーム溶接を最適化するこの例に示されているように, ほとんどの産業用アプリケーションでは, 応力の簡略化された評価が必要です. 溶接部で疲労寿命を予測します. これらの方法は, 規格と設計コードに記載されており, アーク溶接プロセスに焦点を当てています. 抵抗溶接や摩擦溶接などの技術は, 現在これらの規格ではカバーされていません.
このブログでは, これらの溶接方法のいくつかを解析して, 溶接内および溶接周辺の応力分布を評価し, これをCOMSOL Multiphysics でモデル化する方法を示します.
溶接と疲労
疲労とは, 損傷を受けていない状態で材料の破壊応力をはるかに下回る繰り返し荷重を受ける材料に亀裂が発生し, 最終的には成長して部品の破損を引き起こすプロセスです. 破損までのサイクル数は, 材料の弾性特性と荷重だけでなく, 残留応力, 材料の破壊靭性, 不連続性, 粒子サイズ, 温度, 形状, 表面仕上げ, 腐食の有無などのさまざまな要因にも依存します. 溶接はこれらの要因のほとんどすべてを局所的に変更するため, 溶接内およびその周辺の疲労寿命の予測が多くの関心と研究の問題であることは当然のことです.
荷重の性質と繰り返し荷重を受ける材料のタイプに基づいて疲労寿命を予測するために使用されるさまざまな方法があります. サイクル数が多い場合, これらの方法のほとんどは, 材料の S-N 曲線を使用します. これらの曲線は, 応力のレベルと亀裂が検出されるまでのサイクル数との関係を示しています.
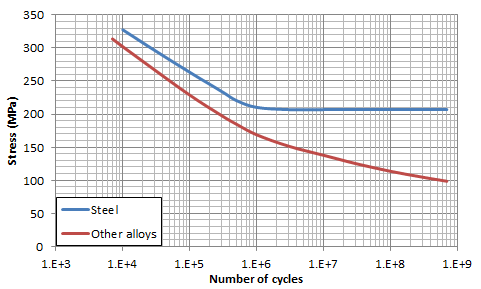
グラフは, 2つの合金ファミリーの典型的な S-N 曲線を示しています. 鋼合金には通常, 耐久限度があり, それを下回ると疲労破壊が発生することはありません. 他の合金にはそのような耐久限度がない場合があり, どのレベルの応力でも最終的には故障の原因になります.
上の図が示すように, 応力の10%の変動は, 破損までのサイクル数2倍以上の差を意味する可能性があります (または鋼合金ではさらに大きくなります). したがって, 溶接部の疲労寿命を予測するには, 溶接部の応力を高い信頼度で決定することが重要です.
溶接形状を見る
溶接は通常, 結合される部品の相対位置によって分類されます. この例では, 2つの部品が斜めに結合された溶接であるフィレット溶接を解析します. フィレット溶接は, パイプ, 垂直プレート, またはオーバーラッププレートを結合するときに使用される一般的なソリューションです. フィレット溶接は, ルートへの完全な融合を実現し, 許容できると見なされる長さ全体で最小寸法 (スロートの厚さまたは脚の長さの観点から) を示すために必要です.
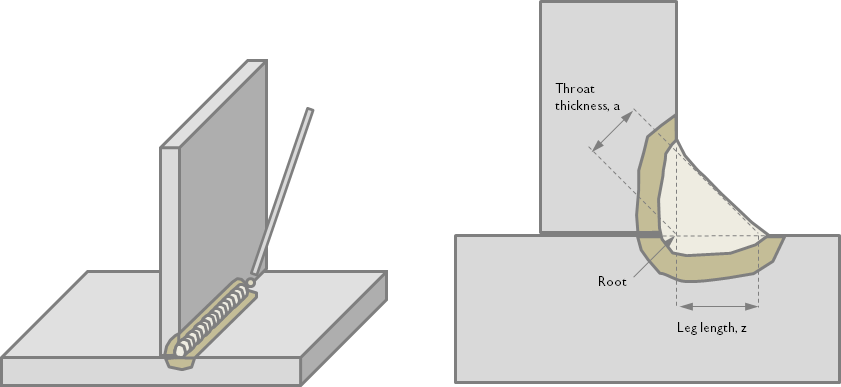
フィレット溶接の溶接プロセスの概略図. 溶接 (ライトグレー) は, 溶接パラメーターと材料に応じて, 凹面または凸面を示します. 熱影響部または HAZ (カーキ) は, ベース材料 (ダークグレー) とは異なる材料特性を持っています.
溶接の品質は溶接パラメーター (溶接速度, 部品の予熱, 溶接ツールの相対位置, 溶接電流など) に非常に敏感であるため, 溶接が完了したら, 溶接の解析を実行するのが一般的です. 溶接の品質を評価するために, 目視解析から超音波解析, 染料浸透探傷解析から蛍光浸透探傷解析まで, さまざまな手法を利用できます.
現場で製造されたほとんどの溶接部は, 接合されたプレートの厚さ全体に溶接部が完全に浸透することを保証するのに十分な解析を受けることができません. これが, 溶接スロートのみを荷重経路として使用し, 溶接の応力解析を行う際に母材が溶接継手の剛性に寄与しないと想定することが極めて一般的である理由の1つです.
公称応力法
ユーロコード (EC) や国際溶接協会 (IIW) などの規格では, 設計者が公称を使用することを認めています. この方法は, 特定の材料と形状にのみ適用され, 溶接部で計算された等価応力または公称応力を使用し, この応力を各詳細カテゴリに定義された経験的 S-N 曲線と比較します.
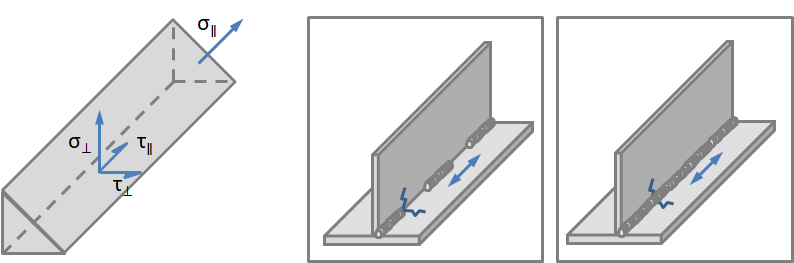
溶接部の等価応力と2つのカテゴリの計算に使用される応力成分.
この方法は簡便であるという利点がありますが, 一連の制限があります. 規格に記載されていない材料や構成細部には適用できませんし, 記載されている場合でも, 溶接継手のクラスを判断することが困難な場合があります. また, 溶接継手は規格に記載されている箇所とは異なる箇所に疲労亀裂が発生することがあります. このような欠点があるにもかかわらず, 本手法はその簡便性から最もよく利用されています.
IIW 規格では, 荷重が複雑な場合, 有限要素法 (FEM) を用いて公称応力を求めることが認められています. この場合, 比較的単純で粗いモデルで公称応力を決定することができます. メッシュが粗い場合, 応力の過小評価を避けるために, 溶接部を通る断面では要素応力ではなく節点力を使用する必要があります. 修正公称応力 (局所応力) を計算する際には, 溶接継手の構造的な詳細から生じる応力集中の影響をすべて排除するように注意する必要があります.
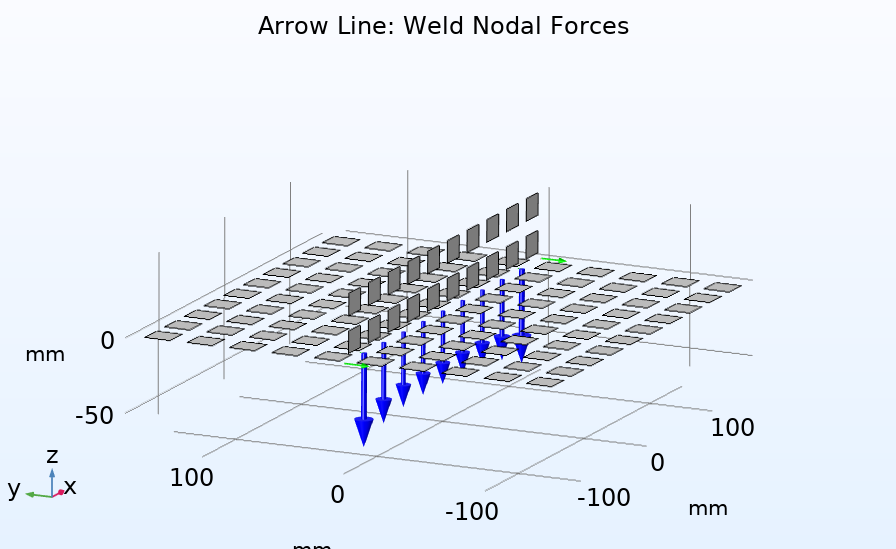
荷重分布を決定する最も単純な FEM アプローチは, 溶接部を溶接部品間の連続性として考慮することです. このアプローチは, 溶接部の柔軟性を考慮しないため, 荷重経路として機能する可能性のある溶接部が複数ある場合や, 構造物の全体剛性を決定することが重要な場合は有効ではありません. この方法で測定された節点力を溶接部の応力に変換するために, 何らかの操作が必要になる可能性があるため, 節点力を考慮する際には注意が必要です.
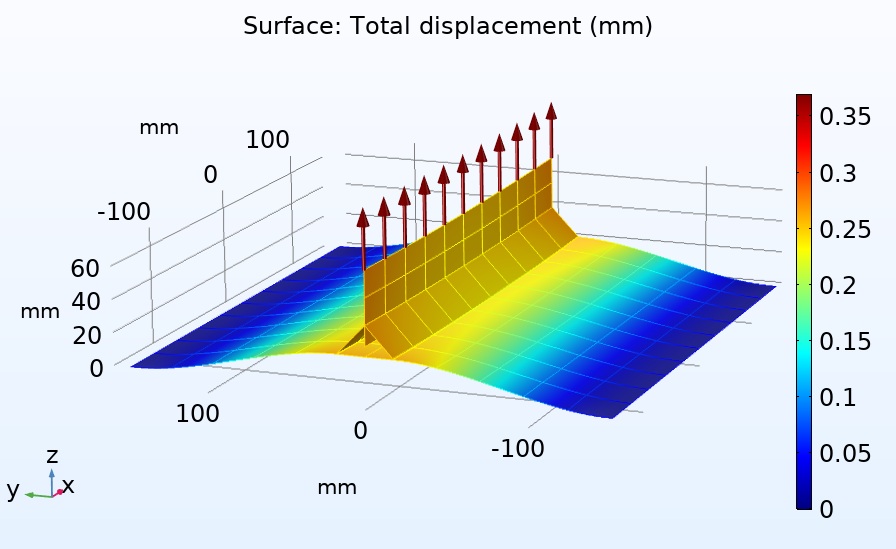
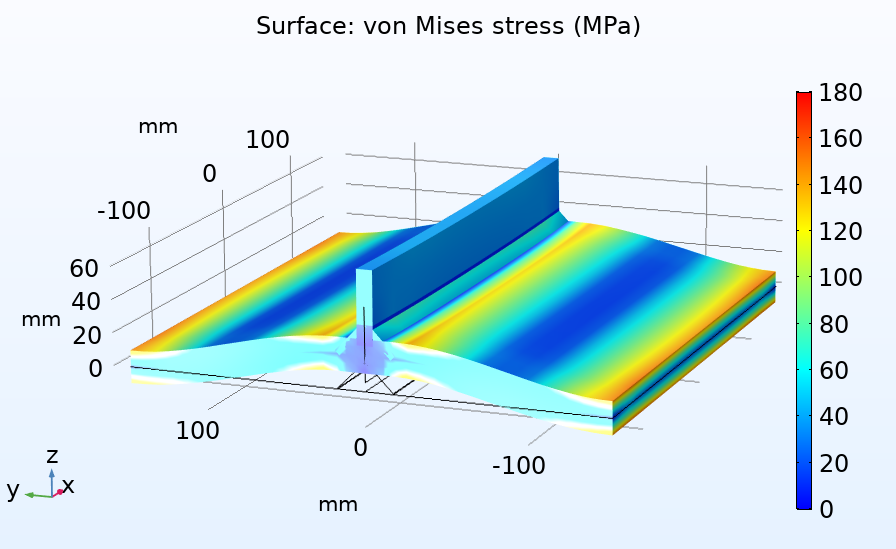
簡略化された溶接解析の例. 加えられた荷重, メッシュ, および変位が左側に表示されます. シェルの3D 表現は, フォン・ミーゼス応力とともに中央に表示されます. 節点力は, わかりやすくするために要素が縮小された状態で右側に示されています.
COMSOL Multiphysics のコンテキストでは, 節点力は反力として解釈できます. 反力は拘束が存在する場合にのみ使用できるため, 連続性条件で結合されたアセンブリを使用できます.
溶接ジョイントを表すより正確な方法は, 実際に個々のスロートをシェルでモデル化することです. この方法では, 溶接スロートの中立面にサーフェスを作成する必要があります. 異なるプレート間の接続は, フィレット溶接の数と, それらが部分的または全体的な溶け込みを示すかどうかによって異なります. この方法は, スロートの柔軟性を捕獲するため, グローバル構造の荷重経路と剛性を解析するのに適しています.
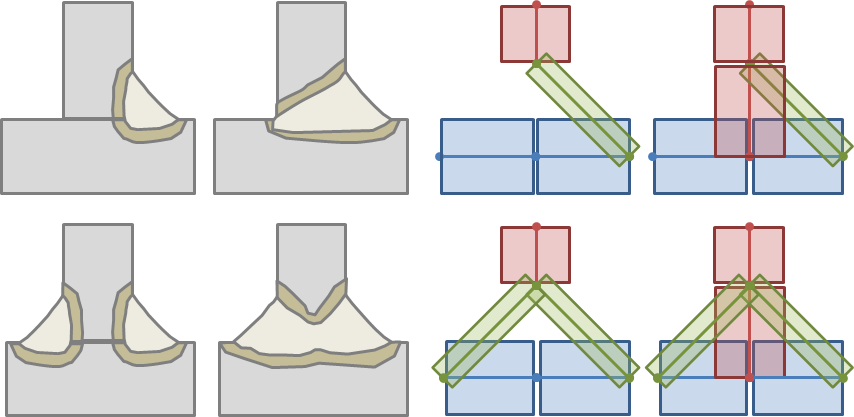
左側に4種類の溶接, 右側に同等のシェル表現. シェルの厚さは透明なボックスで表されます.
部分溶け込みの2つのフィレット溶接を示す溶接継手の例を以下に示します. 下の図に示されているように, この表現は溶接応力をより広い領域に分散させるため, コンプライアンスと溶接周辺の応力が減少します. 溶接スロートを具体的に表すもう1つの利点は, 節点力を直接使用して公称溶接応力を導出できることです.
溶接スロートがメッシュで表される溶接解析の例. 加えられた荷重, メッシュ, および変位が左側に表示されます. シェルの3D 表現は, フォン・ミーゼス応力とともに中央に表示されます. 節点力は, わかりやすくするために要素が縮小された状態で右側に示されています. 矢印のカラースケールと大きさは, 前の画像と同じです.
公称応力法は, 溶接部の疲労寿命を計算するための比較的単純で安価な方法であり, COMSOL Multiphysics を使用して荷重と応力分布を取得するのに非常に適しています.
効果的なノッチ応力法
溶接継手の疲労寿命を計算する別の方法は, 溶接の最終的な形状を解析することです. これを実効ノッチ応力法と呼びます. この方法では, 構造がソリッドとしてモデル化されている必要があるため, 構造の動作を近似するためにシェルを使用することはできません. この詳細なモデルを使用して計算された応力は, ジョイントのタイプに固有ではない S-N 曲線と直接比較できます. 前述の理由により, 溶接部はその形状に高いレベルの変動性を示すため, この方法では, のど厚と特定のノッチ半径に基づいた効果的な溶接プロファイルを想定しています.
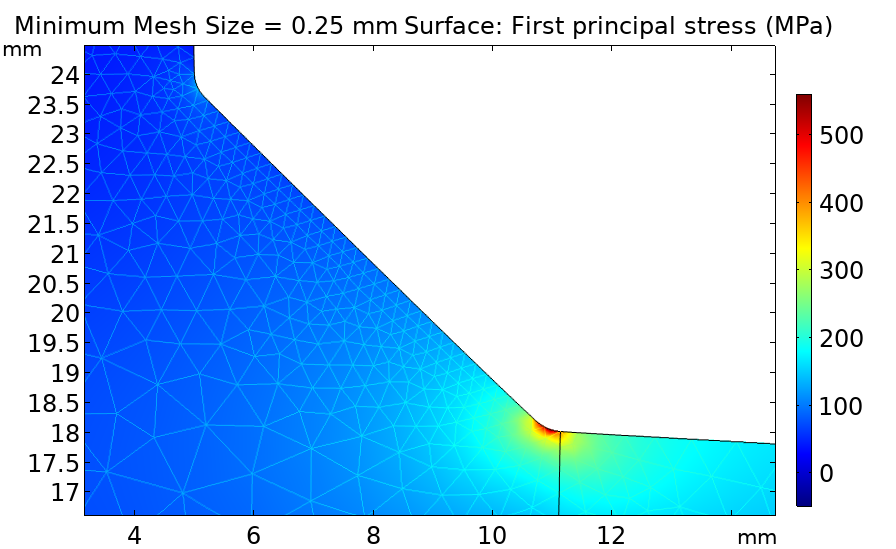
完全溶け込みの両面溶接のモデル. 右側の詳細は, ピーク応力が想定されるノッチ半径1mmとどのように密接に関連しているかを示しています.
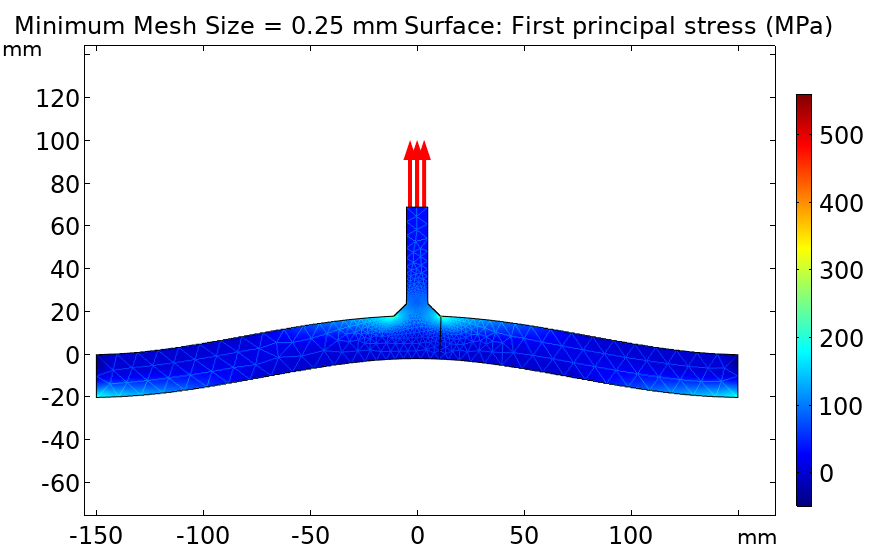
前の図に見られるように, 応力分布は非常に局所的なピークを示しています. これは, メッシュが十分に細かくなければ捕獲できません. 次の図は, 最小メッシュサイズの関数としてのピーク応力を示しています.
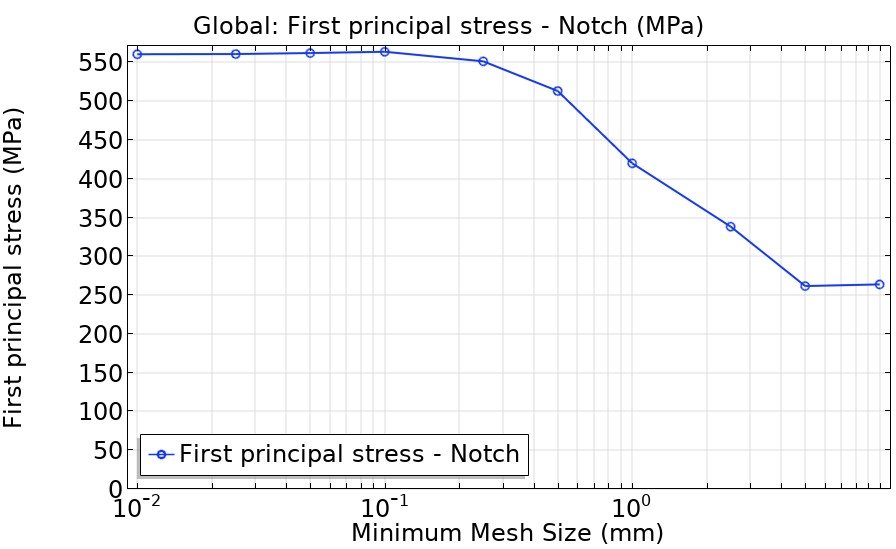
さまざまなメッシュサイズに対して計算されたノッチでの最大主応力.
上に示したように, ピーク応力を正しく捕獲するには, この例では0.25 mmより細かいメッシュが必要であり, 厚さ20mmのプレートと厚さ10mmのプレートを結合します. ノッチ応力法では, 非常に詳細なメッシュが必要であり, 実際の問題への適用が制限される可能性があります. 次に, サブモデリングは, 大きな形状の局所的な応力集中を決定する効率的な方法を提供します.
ホットスポット法
溶接継手の疲労寿命を計算する別の方法は, ホットスポット法です. この方法は, 溶接部周辺の理想的な応力分布から導き出される代表的な応力に基づいています. この代表的な応力は, 構造応力, 幾何学的応力, またはホットスポット応力と呼ばれることもあります. これは, 以下で使用される単位です. 一般に, トウの近くの溶接に垂直な応力は, 厚さに沿って非線形分布を持ちます.
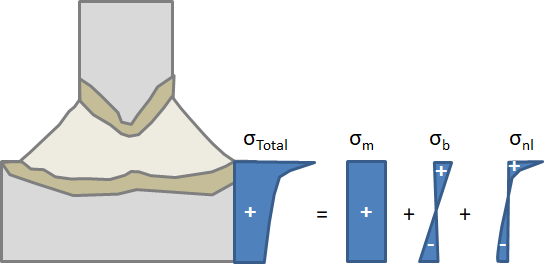
厚さによる全応力と, メンブレインへの分解, 曲げ, および非線形応力.
厚さ全体の応力分布は, 次の3つの部分に分けることができます:
- 厚さに沿って一定である膜応力
- 厚さ全体に線形に分布し, 自己補償される曲げ応力
- 非線形応力. これも自己補償されます
ホットスポット法は, 膜応力と曲げ応力を組み合わせたときに得られる表面応力です. 以前のモデルと COMSOL Multiphysics で利用可能な応力線形化機能を使用して, 厚さ全体の応力分布をプロットできます.
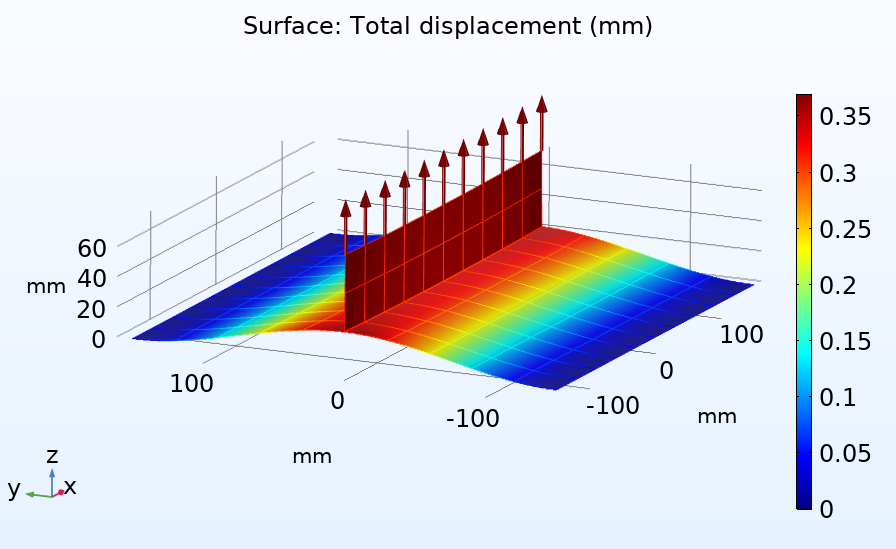
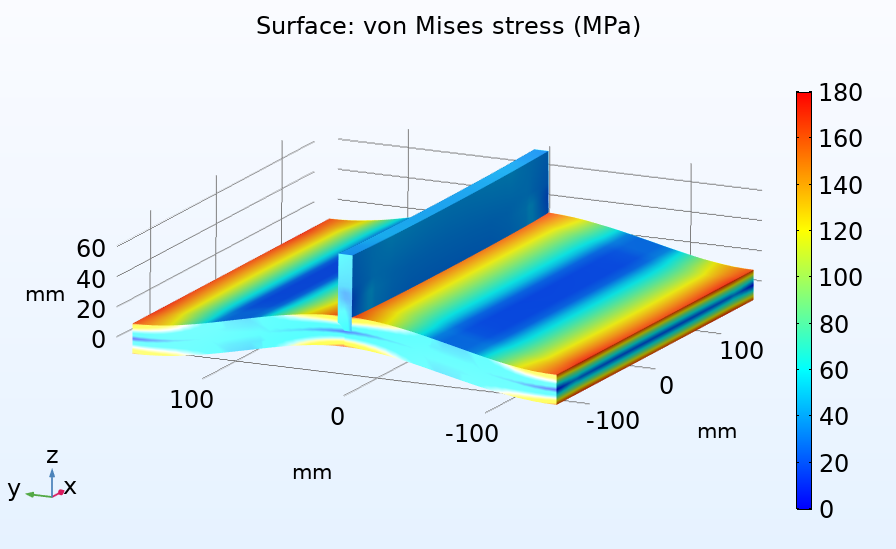
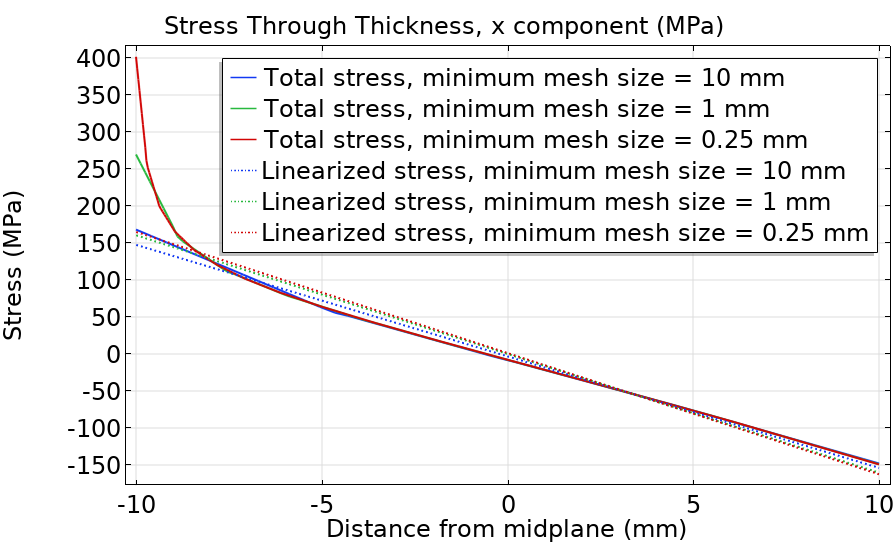
厚さ方向の応力分布を評価するために使用されるパス (左). 厚さ全体の応力分布と, この分布がメッシュサイズによる変化 (右).
前の図からわかるように, 厚さ方向の応力分布はメッシュサイズによって大きく異なりますが, 膜と曲げ応力の組み合わせは, 粗いメッシュの場合でもほぼ一定のままです. このアプローチでは, 厚さ方向の応力分布を取得するために, 構造をソリッドとしてモデル化する必要があります.
同じホットスポット応力を計算する別の方法として, 隣接する領域からの表面応力を外挿する方法があります:
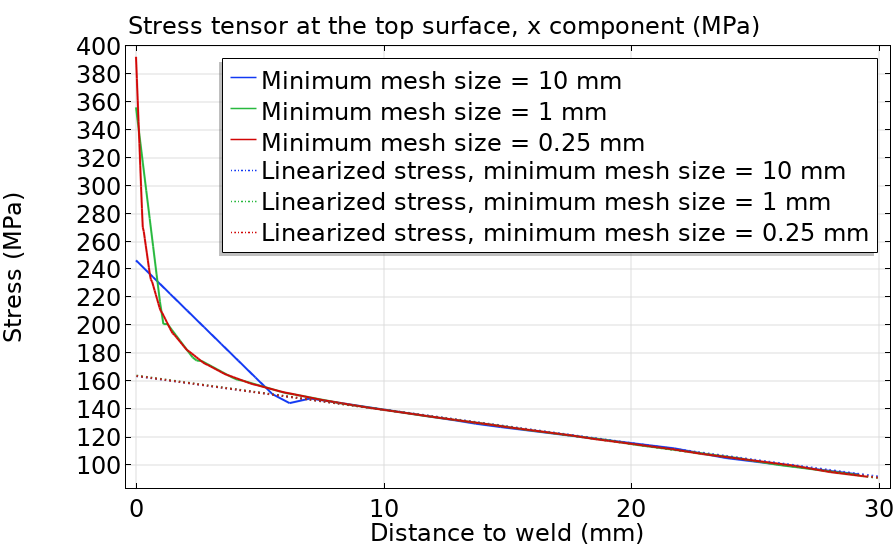
表面の応力分布を評価するために使用されるパス (緑). 表面応力と, この分布がメッシュサイズによってどのように変化するか (右). 線形化された応力は, この例では溶接止端から10mmおよび20mm離れた場所の応力に基づいています.
ノッチ応力はメッシュサイズに強く依存しますが, 溶接部から特定の距離での応力分布はすべてのメッシュサイズで同じであることが再度確認できます. つまり, このアプローチでは粗いメッシュサイズまたはシェルモデリングを使用でき, 得られるホットスポット応力は, 溶接のソリッドモデリングと非常に細かいメッシュで得られるものと同じくらい正確になります. この方法では, 溶接から特定の距離にノードと要素が配置された通常のメッシュが必要です. これには, モデルでの設定に時間がかかる場合があります. ホットスポット応力を推定するために応力を取得する必要がある距離は, 通常, 規格で定義されており, 溶接部品の寸法とメッシュサイズによって異なります.
溶接部の疲労寿命に関する最終的な考察
これまで述べてきたように, 溶接継手の疲労評価にはいくつかの方法があります. このブログでは, COMSOL Multiphysics がどのような方法で利用できるのか, また, それぞれの方法の利点と欠点について解析しました.
| 方法 | メリット | デメリット |
|---|---|---|
| 公称応力 |
|
|
| ノッチ応力 |
|
|
| ホットスポット応力 |
|
|
次のステップ
COMSOL Multiphysics が溶接および疲労解析のニーズにどのように適合するかについての詳細をご覧ください. ソフトウェアの評価については, お問い合わせください.





コメント (0)