弾性波でモデルを構築する場合, 既定の荷重が存在する部分がありますが, 合理的に適用できる制約はありません. このような場合, ジオメトリに応じて, さまざまな戦略があります. これらのさまざまなアプローチの使用方法とそのニュアンスを見てみましょう.
弾性波の問題
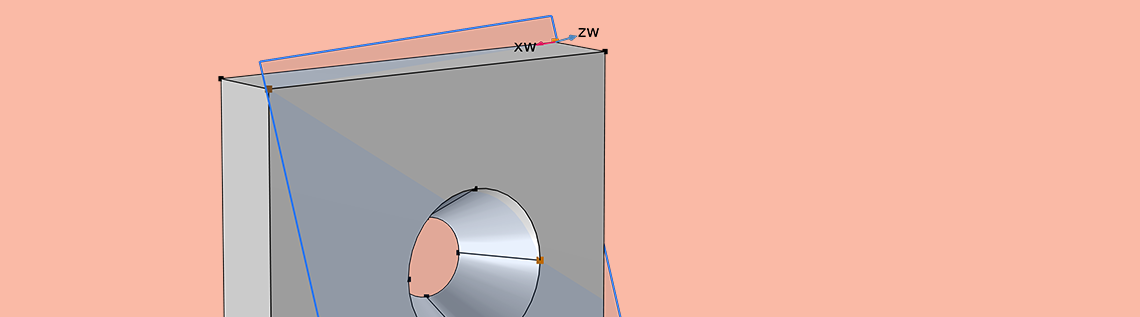
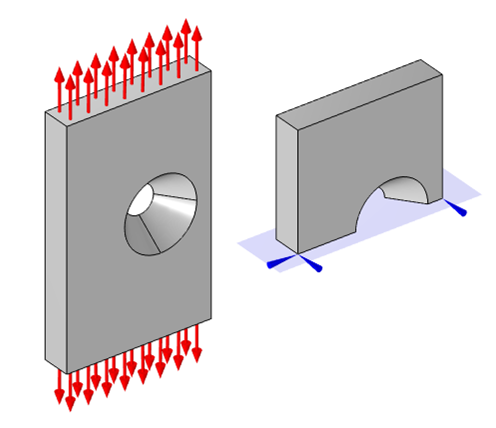
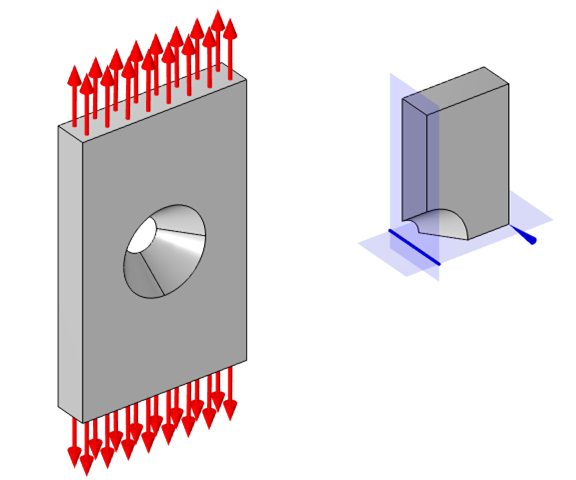
まず, 穴の開いた平板の単純なモデルを検討します. これは, 弾性波の古典的な問題です. 上部と下部に等しく反対の力が加えられていると仮定しましょう. おそらく, この部分がいくつかの固定具を介していくつかのケーブルに接続され, 張力がかかっていると想像してください.
引張荷重下の中央に穴のある平板の自由体図.
固定具とケーブルのモデル, およびケーブルが接続されているもののモデルを作成することはできますが, これは必要以上の労力を必要とします. 私たちは, より大きな系の中のこの1つの部分に集中して解析を行いたいだけなので, これらの他のすべての部分をプレートの端に垂直な境界荷重として近似することは理にかなっています.
これで, 等しい力と反対の力がかかっているパーツには加速度が発生しないことが直感的にわかりました. そのため, パーツは変形しますが, 動きません. つまり, パーツがどこにあるか, またはパーツがどのように方向付けられているかがわからなくても, この問題に対する定常的な解決策が存在すると自信を持って言えます. つまり, 加えられた力は任意の方向に揃えることができ, 応力とひずみに関する解は同じです.
現在, 有限要素法を使用して弾性波問題を解く場合, 応力やひずみを直接解くことはありません. 代わりに, 変形していない状態からの変位(または変形)を求解します. 応力とひずみは, 変位場から計算されます. このブログでは, 線形の場合のみを取り上げるだけで十分ですが, より高度なトピックに興味がある場合は, 次のブログを参照してください.
変形の求解策を得るには, 変位場に一連の拘束を導入する必要があります. これらは, すべての自由体の変位と回転を拘束するのに十分でなければなりませんが, 応力とひずみに影響を与えることはできません. このブログでは, 扱っているジオメトリに応じて, これを実現するさまざまな方法について説明します.
対称面の使用
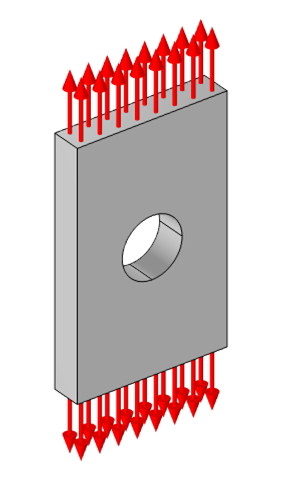
このジオメトリの場合, 経験豊富な構造解析技術者は, 利用できる対称面が3つあることにすぐに気付くでしょう. グローバルデカルト座標系に合わせてパーツを描画し, xy平面, yz平面, およびxz平面に平行なワークプレーンに沿って分割を使用できます. これにより, モデルが元のモデルの1/8サブモデルに縮小されます. これらの平面に沿った3つの面に対称条件を適用すると, パーツを完全に拘束する効果があります. さらに, これには, モデルの計算サイズを削減するという有益な副産物があります.
3つの直交する平面に沿った対称性を利用すると, モデルが完全に制約されます.
これらの3つの対称条件がパーツをどのように制約するかを正確に考えてみましょう. 対称条件は, 選択された(平面)境界に対して法線方向に変位がないことを強制します. したがって, xy平面に平行な面に適用される対称条件は, この面のz方向の変位がゼロであり, x軸とy軸を中心に回転できないという条件を課します.
次に, yz平行面の対称条件は, x方向の変位や, z軸を中心とした回転がないという追加の条件を課します. y軸を中心とした回転はもう一度制限されますが, これは問題ではありません.
最後に, xz平行面の対称条件は, y方向に変位がないという追加の制約を課します.
したがって, 変位と回転に3つの直交拘束のセットを適用したので, パーツは十分に拘束され, モデルを解くことができます. 結果を可視化するには, 3つのミラー3Dデータセットのセットを使用すると便利です. これにより, 平面に関する任意のデータセットをミラーリングして, パーツ全体を可視化できます.
対称性のない部品
残念ながら, 私たちは通常, 3つの対称面を持つパーツを持つほど幸運ではありません. 以下に示すように, 穴にテーパーを導入し, その位置を変更して, パーツを変更してみましょう.
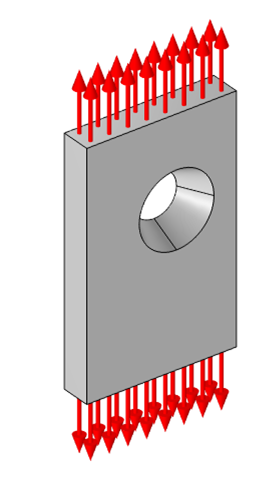
中心がずれた先細りの穴がある張力下の平板の自由体図.
この場合, 対称性を利用する方法はありません.では, 何ができるでしょうか. 実際に私たちが取ることができる4つの異なるアプローチがあります!
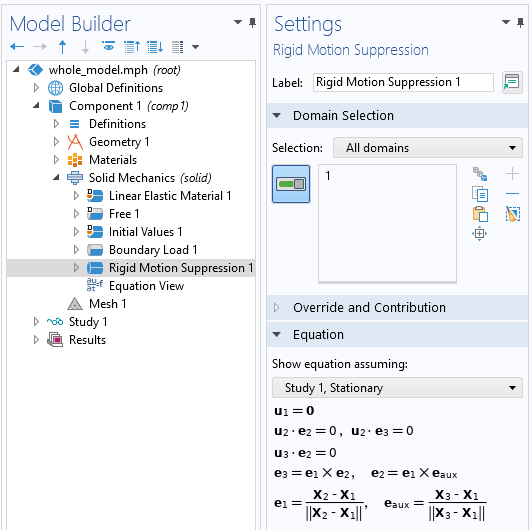
剛体運動抑制機能をすべてのドメインに適用して, 変位と回転を制限します.
最初の最も簡単なアプローチは, 剛体運動抑制ドメイン制約機能を使用することです. この機能は, モデルの1つまたはすべてのサブドメインに適用する必要があるだけであり, すべての剛体の変位と回転を削除する一連の制約を舞台裏で適用します. この機能を適用するだけで, モデルを求解します.
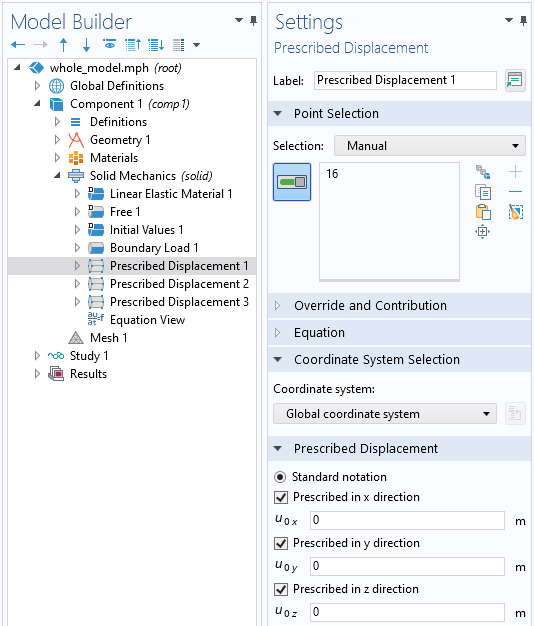
すべての自由体変位を制約する既定変位点条件.
2番目のアプローチは, 3つの異なる点拘束のセットを介して変位と回転を手動で拘束することです. これを行うには, ジオメトリ上の点を選択することから始め, その点にx, y, およびz変位をゼロに設定する既定変位条件を課します.
選択するポイントは任意ですが, この長方形のパーツのコーナーの1つでポイントを選択するのが最適であることがすぐにわかります. この単一の拘束は, すべての剛体変位を除去するのに十分であり, 応力およびひずみ場に影響を与えません.
すべての自由体の回転と変位を拘束するが, ひずみ場には影響を与えない3点変位拘束の可視化.
次に, 3つの直交軸を中心とした回転を削除する必要があります. これは少し難しいかもしれませんが, この場合, ジオメトリがグローバルデカルト軸に位置合わせされているという点で幸運です. したがって, 完全に拘束された点から開始して, デカルト方向に沿って見ることができます.
まず, この点から別の点が見つかるまでx軸に沿って見てみましょう. そこで, 別の既定変位条件を適用して剛体の回転を削除しますが, ひずみや応力に影響を与える拘束を課さないようにする必要があります. 別の言い方をすれば, これら2点間の距離に制約を課したくないということです. したがって, この2番目のポイントでは, y方向とz方向の変位を拘束しますが, x変位は拘束しません. この拘束は, それぞれz軸とy軸を中心とした回転を削除します. これで, パーツはx軸を中心に自由に回転できるようになり, もう1つの点拘束を使用してこの自由度を削除できます.
元の完全に拘束された点に戻ると, 点が見つかるまでy軸またはz軸のいずれかに沿って見ることができます. z方向に沿って検索してみましょう. ポイントが見つかったら, y方向の変位がゼロになるように既定の変位条件を適用できます. これにより, x軸を中心としたパーツの回転が防止されます. 繰り返しますが, これらのポイント間の距離を制限していないことを確認する必要があります. 誤ってそうすると, 局所的に高い応力が発生します.
この2番目のアプローチは, 実際には, 最初のアプローチによって自動的に実行されていることを手動で実装したものです. ただし, 疑問が生じる可能性があります. デカルト軸に3つのポイントを揃えないとどうなりますか?剛体運動抑制の最初のアプローチを使用する場合, その機能は, 平面を形成する任意の3つのポイントを自動的に選択し, 一貫した一連の拘束を適用することができます. また, 平面を表す限り, 3つのポイントをどのように使用できるかを見てみましょう.
3番目のアプローチでは, 同じジオメトリで作業しますが, デカルト軸と位置合わせされていない3つのポイントを使用して拘束します. 最初にワークプレーンを定義し, 次にそのワークプレーンを使用して座標系を定義し, 最後に既定の変位条件内でその座標系を使用する必要があります.
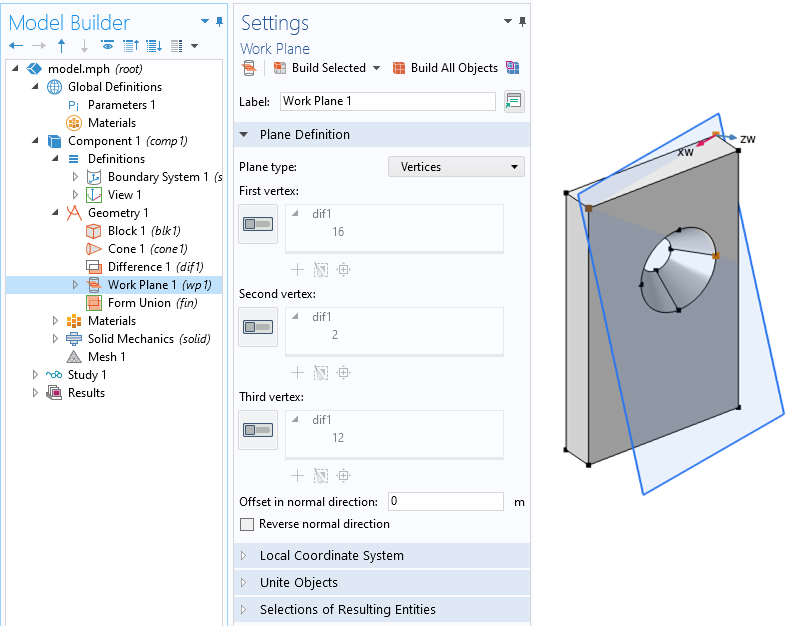
3つの任意の点を使用して, 新しいワークプレーンを定義.
ジオメトリ内で平面タイプの頂点の新しいワークプレーンを定義することから始め, 平面を定義し, 同一直線上にない3つのポイントを選択します. 選択した最初の2つの頂点が, この平面の最初のローカル軸を定義することに注意してください. 次に, ジオメトリから座標系を定義します. この座標系のフレームを空間に設定し, ジオメトリ設定からシステムで新しいワークプレーンを選択します.
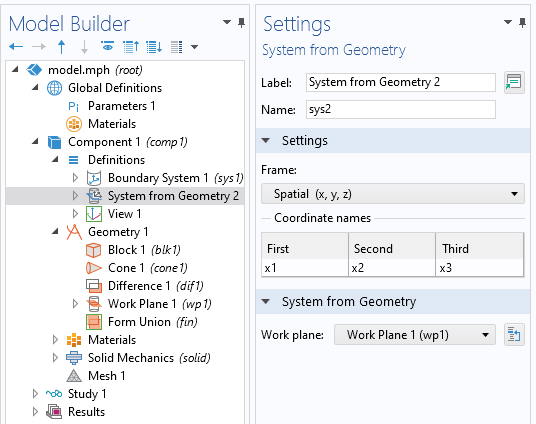
ワークプレーンに基づいて座標系を定義します.
次に, 前と同じように, 3つの既定変位点条件を追加し, それぞれについて, 座標系をジオメトリからの系に設定します. これらの3つのポイントは, ワークプレーン機能内で選択された3つのポイントに対応している必要があります. 最初のポイントで, 3つの変位すべてを拘束します. 2番目のポイント(最初のローカル軸を定義するポイント)で, 2番目と3番目の方向の変位を制限します. 3番目の点で, 3番目の軸(平面に垂直)方向の変位を拘束します. このアプローチの利点は, パーツをデカルト軸に揃える必要がないことです. この場合も, 剛体運動抑制機能は同等の機能を提供します.
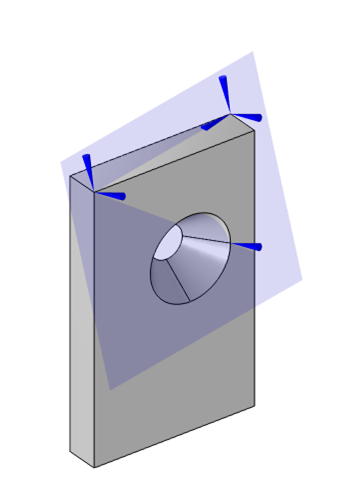
これらの3点によって定義される座標系で, すべての自由体の回転と変位を制約する3点変位制約の可視化.
4番目のアプローチは, 平面を定義する3つのポイントを持たないジオメトリの特殊なケースに対処します. これは, 元のメッシュにポイントが定義されていない椎骨モデルのように, インポートされたメッシュファイルを処理しているときに発生する可能性があります. インポートされたメッシュ上に手動で頂点を作成することは可能であり, ジオメトリのエッジを分割して追加のポイントを導入することも可能ですが, この最後の方法について知っておく価値があります.
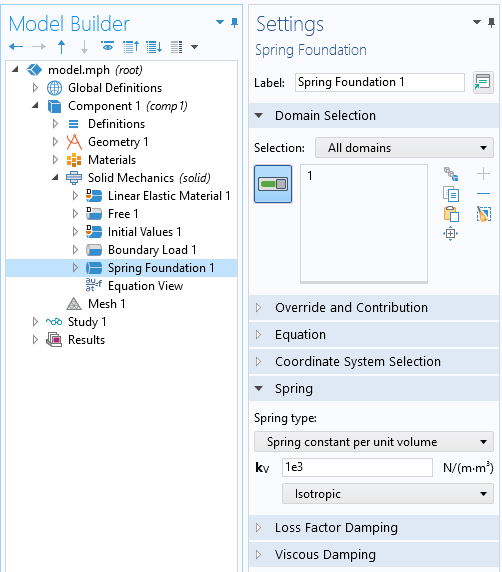
スプリングファンデーション機能を使用すると, 変位と回転も制限されますが, ばね定数が十分に小さい場合は解に影響しません.
この4番目のアプローチでは, スプリングファンデーション機構のドメイン機能を使用して, モデルのすべての領域に適用します. この機能は, 変形していない位置と比較して, 構造モデルのあらゆる自由度で人工的な追加の剛性を導入します. このばね定数の大きさは, モデル内の調整係数です. 小さすぎると, 十分な数値剛性が得られず, モデルは求解されませんが, 結果にも影響するため, 大きすぎないようにする必要があります. 実際には, 非常に低い値から始めて, モデルが求解するまで値を大きくします. このテクニックが必要とされるのは非常にまれなケースですが, それでも知っておく価値があります.
部分対称のパーツ
また, 対称性のあるパーツの非常に一般的な状況についても考えてみましょう. この場合, 剛体運動抑制機能は使用できません.
半分の対称性を利用するには, 平面内の移動と平面に垂直な軸を中心とした回転を取り除く2点の変位制約が必要.
モデルの対称面が1つの場合(または平行な2つの対称面がある場合)は, 平面上の2つの点を選び, 所定の変位点条件を使って, その平面内での変位とその平面の法線を中心とした回転ができないように拘束しなければなりません. 対称性のある2つの平面が互いに角度をなして存在する場合, 平面上の1つの点を選び, 2つの平面の交線で記述される方向に移動できないように拘束します.
2つの対称平面を使用して, 単一の点拘束を介して平面の交線に沿った平行移動を削除します.
このようなモデルの結果を提示するという観点からは, 変位の可視化を中央に配置する方法を知っておくのもよいでしょう. 穴を中心とした変位でモデルを可視化するとします. 私たちにできることは, 平均的なコンポーネントカップリング演算子を導入し, それを穴の境界を越えて定義することです. 次に, 変位した結果を可視化するときに, 下のスクリーンショットに示すように, 変位サブ機能でこの平均化された位置を差し引くことができます.
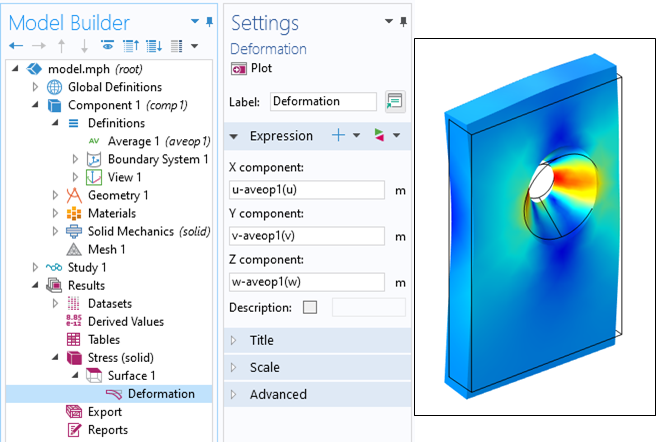
平均演算子を使用して, 穴の中心の周りの変位の可視化を再確認.
制約のない部品のモデリングに関する結論
要約すると, 3Dパーツのモデリングに使用する一連の手法を示しました. ここでは, 一連の平衡荷重のみがあり, 制約はありません. 最も簡単なアプローチは, 剛体運動抑制機能を使用することですが, 他の対称条件のために, ポイントの集合を介して制約する必要がある場合があります.
2D構造モデルの場合, 同様ですがより単純なアプローチが適用されます. 対称性のないパーツの場合, 1つの点をxy平面に完全に拘束し, 別の点を拘束して, 面外のz軸を中心とした回転を防止する必要があります. 1つの対称面または平行な対称面を持つ2Dモデルの場合, 対称面に沿った動きを防ぐために必要な点変位拘束は1つだけです. 対称面が交差する2Dモデルの場合, 追加の制約は必要ありません. 2D軸対称モデルの場合, z方向(対称軸に平行)に沿った変位のみを任意の1点で拘束する必要があります.
これらの手法は, 熱膨張に関連する問題を処理する場合に特に役立ち, 定常, 時間領域, 周波数領域, 固有振動数など, あらゆるスタディタイプで使用できます. これらの方法は, すべての構造解析技術者にとって強力なツールです.




コメント (0)