
結果として生じる電場, 熱損失, 温度変化を計算する目的で, 非正弦波とはいえ周期的な電気信号のモデリングに興味を持つ状況は数多くあります. 一例として, 電気パルス列は, 神経調節, エレクトロポレーション, または熱切除の目的で人体組織に適用することができます. このような信号は時間領域モデリングによってシミュレーションできますが, フーリエ変換アプローチによって線形応答を効率的に計算することも可能です. 詳しく見てみましょう!
目次
はじめに
前回のブログ “過渡電磁励起オプションの理解” で使用したサンプルモデルを引き続き使用していきます. そして, 電流インターフェースを使用してそれを求解します. (このインターフェースは前回のブログで紹介され, この種のモデルを解くのに十分であることが示されています). 電流励振は周期1 µs の台形パルス波形です. このモデルは時間領域で解くことができます. モデル内の端子電圧と全損失を以下に示します.
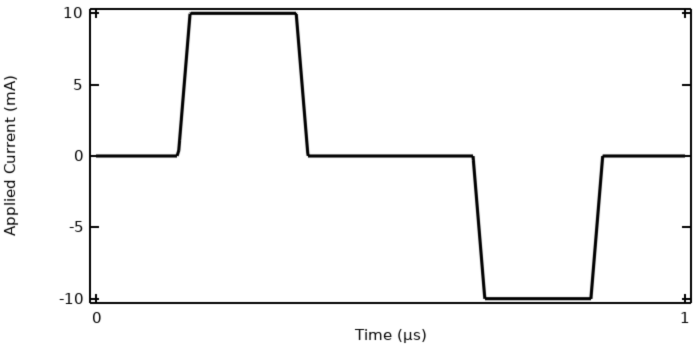
モデルへの印加電流は, ランプ状の台形パルス波.
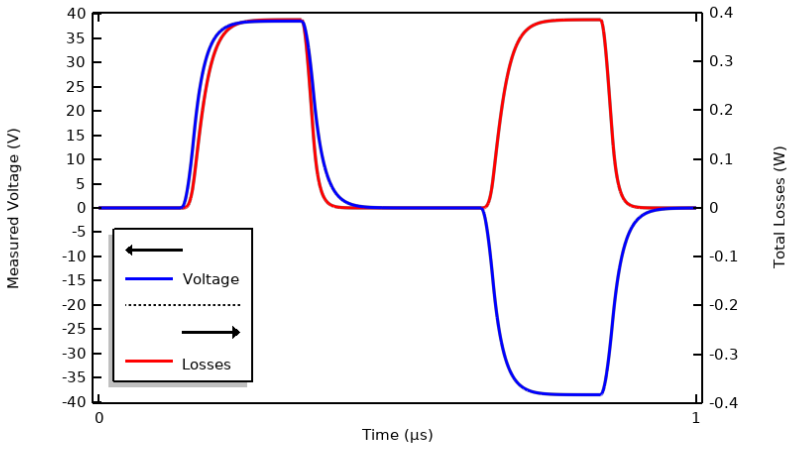
1周期における端子電圧と材料内の損失を計算.
また, モデルを拡張して温度を解析し, 電気伝導率を温度の関数にすることで, 双方向連成マルチフィジックスモデルに変えることもできます. 使用する式は \sigma (T) = 0.03\exp \left(-\frac{T-20^\circ \text{C}}{20\text{K}}\right) \text{S/m} です.
固定温度境界条件は, モデリング領域の側面と底面に沿って適用されます. このモデルは1周期 (1 μs) で解析され, その間の温度変化を調べることができます. 下の画像に見られるように, 温度変化はわずかです.
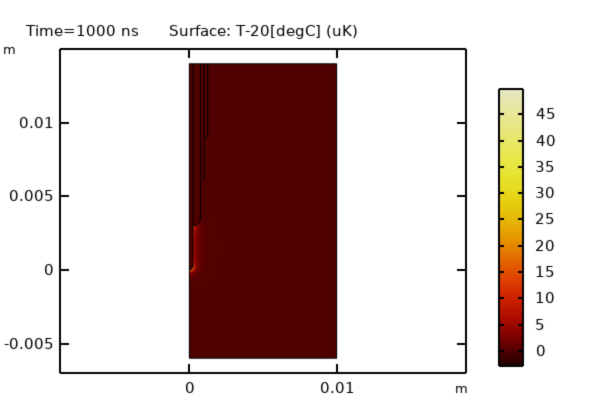
1 µs 後の計算温度変化は小さい.
ただし, 1つの期間よりもはるかに長い時間にわたる温度変化を解析したい場合, このモデリングアプローチでは計算コストが高くなりすぎます. 他のアプローチに目を向ける必要があります. ただし, 本題に入る前に, このモデルと結果について次のいくつかの点に注意しなければなりません:
- 印加される電流はサイクル平均値0を中心に変化するため, 入力信号には DC 成分がない
- 計算された端子電圧と損失はパルス間でゼロ
- 電気伝導率も比誘電率も電場には直接依存しない
- 端子電圧が電流よりも遅れているということは, システムに大きな静電容量があることを意味する
- 1回の励起期間にわたる温度上昇は非常にわずか
電気的な励磁期間と同じような期間にわたって温度上昇が非常に小さいという観測の結果として, 電気的な問題を時間に対して局所的に線形なものとして扱うことができます. これにより, 印加信号のフーリエ変換を行い, 周波数領域モデルを解き, 逆フーリエ変換を使用して電気モデルの過渡結果を再構成することで, 結果を再現することができます. これにより, 入力信号のどの高調波が発熱に大きく寄与しているかについての情報がすぐに得られます.
励起期間よりもはるかに長い時間にわたる過渡的な温度変化を解くには, 入力信号の重要な周波数成分ごとに1つずつ, 複数の電流インターフェースとともに温度場を解く双方向連成モデルを使用すればよいでしょう. これにより, 計算効率が大幅に向上します. ラーニングセンターの記事 “周期信号とその周波数内容について”, “ 逆高速フーリエ変換を使用した過渡信号の再構成”,および “電磁加熱の問題の設定と求解” で説明されているように, このモデリングアプローチにはいくつかの手順があります. これらの手順をここでまとめます.
入力信号の周波数内容を理解する
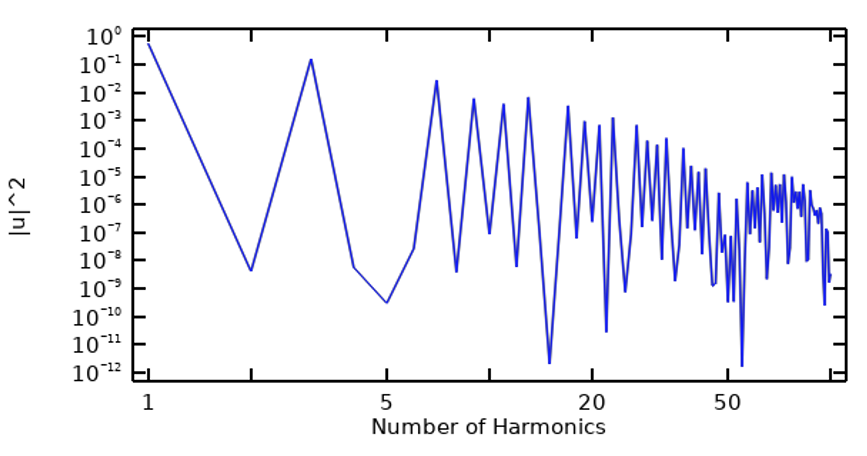
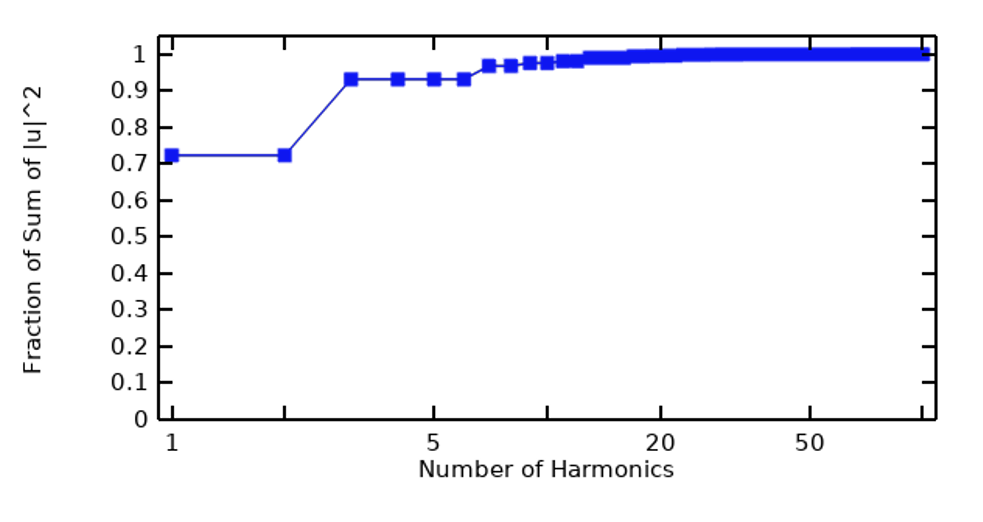
周期的な信号から始めて, その信号の高速フーリエ変換 (FFT) を行い, 周波数内容を調べることができます. これは, 各高調波の大きさだけでなく, 現在の高調波までの累積和でも可能です. 下の図では, 左が台形パルス波の周波数成分のプロット, 右が累積和のプロットです.
台形パルス波の周波数 (左) と累積和 (右).
このような予備段階からわかることは, 少なくともこの例では, 信号のエネルギーの大部分を占めるのは比較的少数の高調波だけであり, ある種の高調波はほとんど寄与していないということです.
周波数領域での解法
印加信号の FFT とともに, 周波数領域の加振に対するシステムの応答も計算する必要があります. これは, システムの応答がすべての周波数で等価になることを意味するものではないことに注意してください. このトピックは, ブログ “電流をモデル化するための励磁オプションについて” で詳しく取り上げられています. 周波数範囲を掃引した結果は, サイクル平均損失のプロットで下図に示されています. この場合, 最初の100個の高調波について解を求め, どの周波数が重要か分かれば, より小さい周波数のセットを実行することができます.
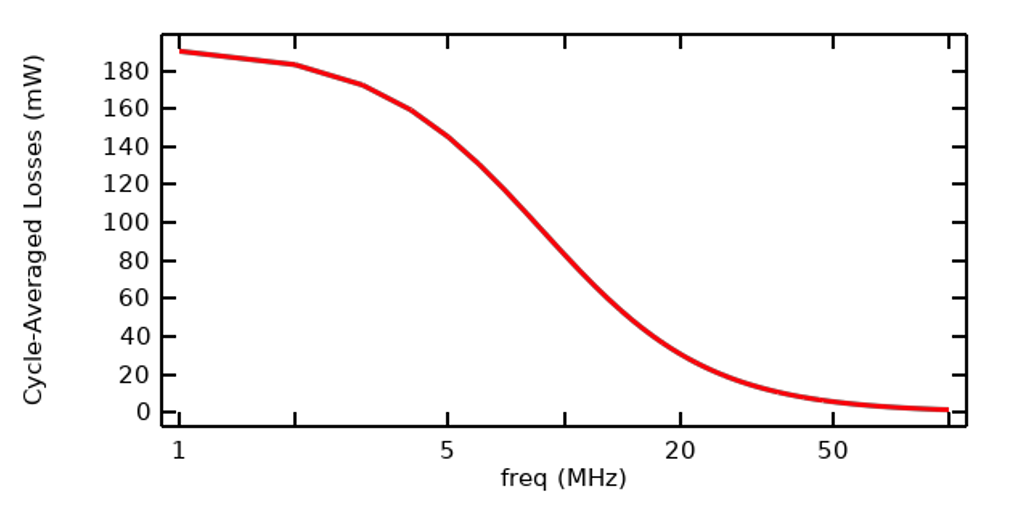
全周波数で等価加振を行った場合の, サンプル内のサイクル平均損失を周波数の関数としてプロットしたもの.
過渡解析結果の再構築
入力信号の FFT はすでに得られているので, すべての考慮周波数にわたって単位加振を行い, 周波数領域の結果を計算したら, 逆高速フーリエ変換 (IFFT) を使ってシステムの過渡応答を再構成することができます. 下のプロットは非常によく一致しており, IFFT 法は計算量が少なくてすみます.
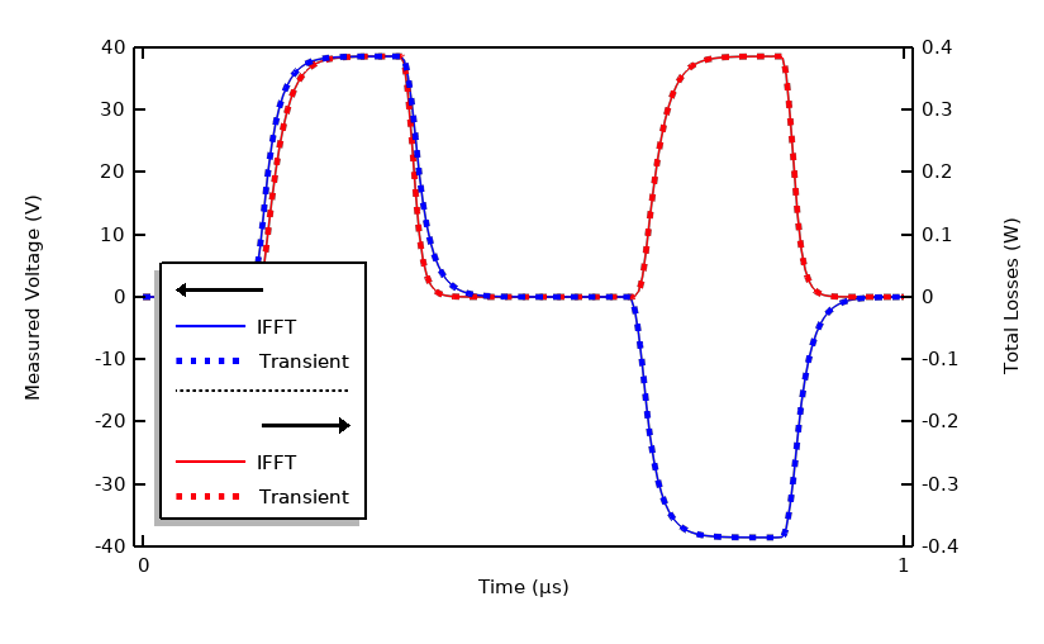
過渡解析結果と100個の高調波を使用した IFFT による再構成結果の比較.
過渡的な結果に関して優れた一致を得ることは有用ですが, 私たちは加熱にしか興味がないことが多いので, IFFT の結果を時間領域での一致で評価するよりも, 1サイクルの時間積分損失を比較することも有用です. この適用信号では, 第1, 第3, 第7, 第9高調波のみを解くことで, 損失の99 % が捕捉されます. つまり, 過渡的な結果が明らかに異なっていても, 積分された損失の合計は非常によく一致しています.
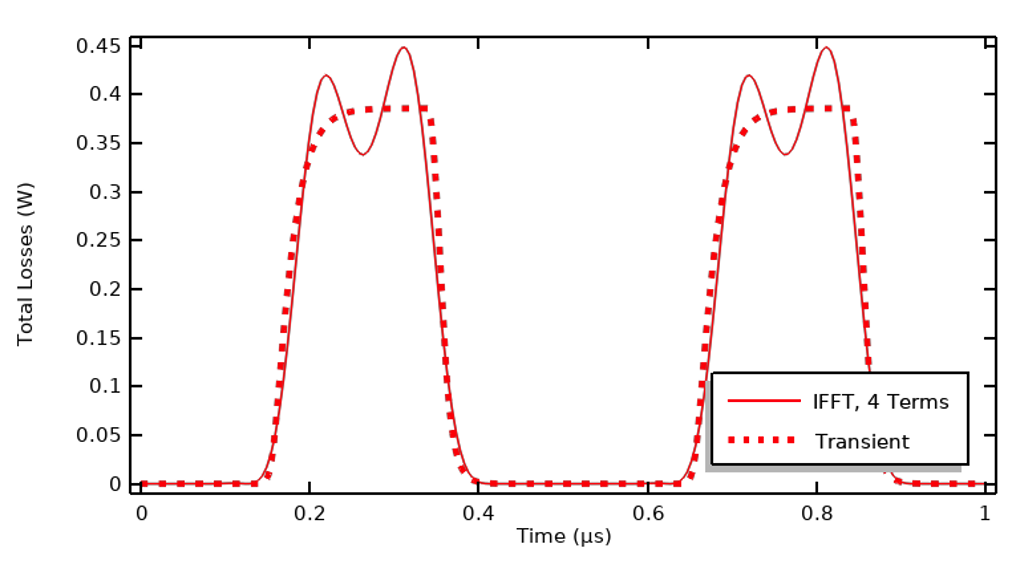
時間領域での損失と, 4つの高調波のみを使用して IFFT で再構成した損失の比較.
上の図では, 一致度はそれほど良くないように見えますが, 全期間の損失の積分は1 % 以内で一致していることがわかります.
FFT 結果の熱解析への利用
これまでのところ, 過渡損失の変動を1周期で再構成する方法について見てきましたが, 熱解析の目的では, 温度変化は電気信号の周期よりも何倍も長い時間にわたって起こるため, もっと長い時間をモデル化することに興味があると思われます. もし電気伝導率が温度によって変化するような材料があれば, このような物理間の双方向連成をモデルに含めたいと考えるでしょう. もし電場と温度場を同時に, 電気的励起を捉えるのに十分な時間分解能で解こうとすれば, 解くのに非常に時間がかかるモデルになってしまいます. それはそれで正当化される場合もありますが, 私たちはより高速なアプローチを望むことが多く, そのような場合に, これまで計算してきたデータが非常に役に立つのです.
以下に示すように, 時間領域の損失は, 最初のいくつかの高調波からの寄与の合計に基づいて, 時間的に一様であると近似することができます. これは, 熱的な時間スケールが電気的な周期よりもはるかに長いという仮定のもとで有効です.
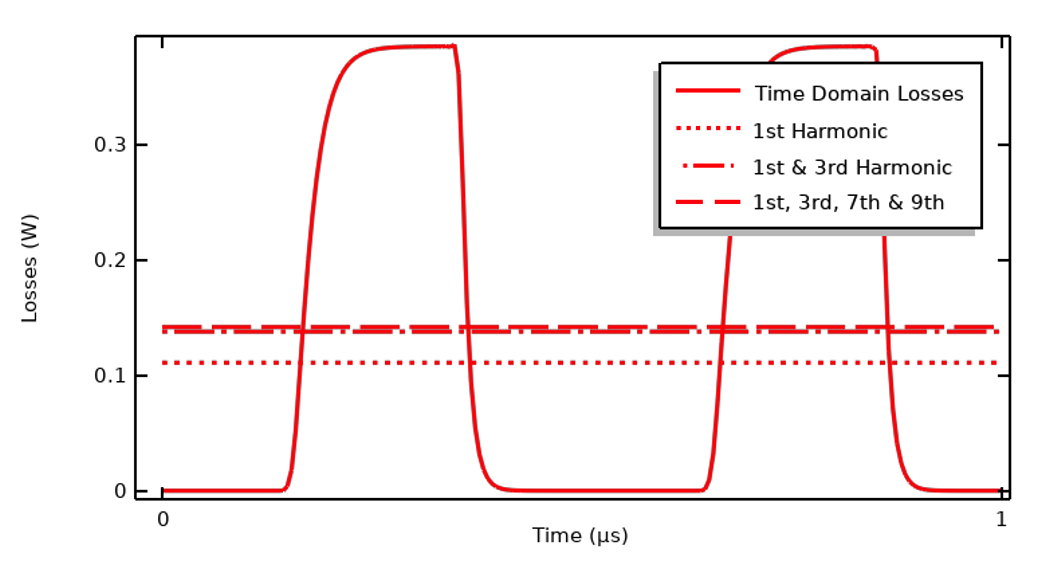
時間領域の損失と, 複数の高調波にわたって計算されたサイクル平均の合計を比較したプロット.
先に観察したように, この入力信号の場合, 1周期の加熱の99 % を捕らえるには, 基本波, 3倍波, 7倍波, 9倍波があればよいのです. つまり, 4つの異なる電流フィジックスインターフェースを持つ新しいモデルを設定し, それぞれを異なるハーモニックに対して周波数領域で解き, 各ハーモニックに対して印加される電流の大きさに入力信号の対応するフーリエ係数を掛けることができます. これらの界面は, 温度変化を計算し, 電気材料特性が温度の関数であることから生じる双方向の結合を組み込む過渡 (または定常) 熱モデルとともに解くことができます. このアプローチは比較的計算効率が高く, 3Dジオメトリのモデリングが可能です. 入力信号の FFT の結果を使用して熱負荷を定義するようなモデルを設定するためのガイドについては, ラーニングセンターの記事 “電磁加熱の問題の設定と求解” を参照してください.

印加電流の高調波の合計によるサイクル平均加熱を使用して, 3Dモデルで計算された温度上昇.
パルスの種類と間隔を変更
また, パルス列 (厳密に正である信号) をモデル化したい場合, 何が起こるかについても取り上げる価値があります. この信号には直流成分があり, 定常解を考慮する必要があるため, 理論的には IFFT がより複雑になります. しかし, 我々は加熱にしか関心がなく, パルス間の損失がゼロになるのであれば, 励起の符号は重要ではありません. つまり, 電流の流れる方向に関係なく, 電気加熱は同じです. 時間経過に伴う加熱がパルス間でゼロに低下する場合, IFFT で考慮する必要のある加熱の直流成分は存在しません. したがって, 厳密に正である入力信号を扱う場合でも, IFFT 再構成を単純化する目的だけのために, 正から負に切り替わる信号として扱うことは合理的です. 以下の信号と先に示した信号は, 計算された損失という点では同じです.
厳密に正である入力信号は, その間に加熱プロファイルがゼロになる限り, 対称的な信号と比較して同一の加熱を持ちます.
パルス間の間隔も変更してみましょう. これにより入力信号の周期が増加するため, FFT をやり直す必要があると考えられるかもしれません. ただし, 元の信号ではパルス間で加熱がゼロになるため, 加熱がゼロになる時間を追加しても単一パルスによる損失は変わりません. つまり, パルス間の時間が長いパルス列がある場合, 加熱プロファイルを正確に予測するには十分であり, 計算量を節約できるため, パルス間の時間が短い信号の FFT を実行するだけで十分です. 双方向連成の熱問題を求解する場合, 印加される信号をデューティ比の平方根の係数でスケールダウンする必要があります. 以下の図では, パルスの持続時間は同じですが, 周期が2倍になっているため, デューティ比は0.5です.
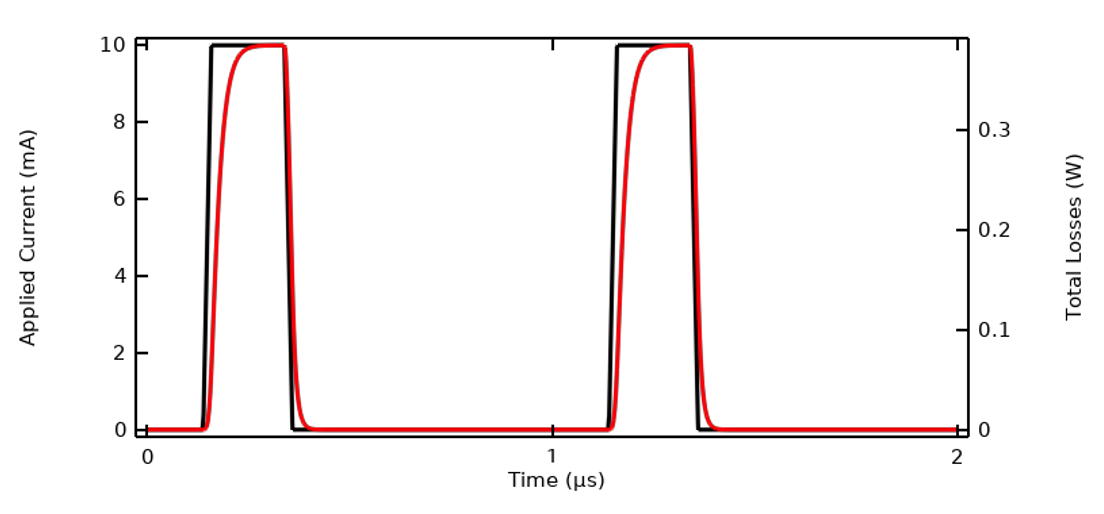
パルス間の時間を増やしても, 各パルスの加熱プロファイルは変わりません.
さらに単純化するために容量性の影響を無視する
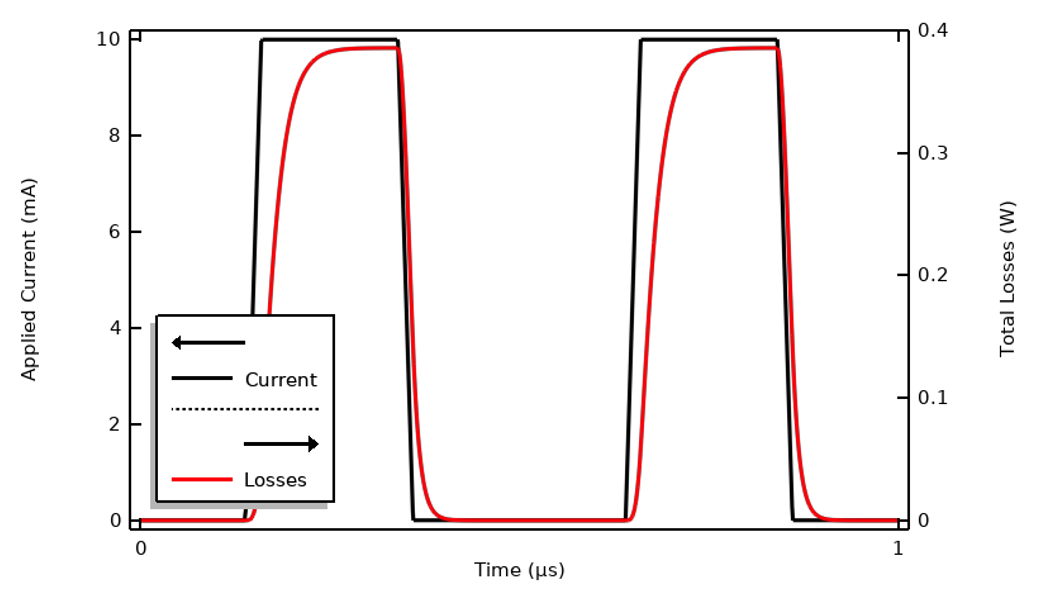
これまでに検討した例は, FFT アプローチが最も有用なケースを説明するために (材料特性と波形の観点から) 設計されました. このレベルの複雑さは必ずしも必要というわけではありません. 印加電流と端子電圧の最初のプロットに戻り, 電気伝導率が10倍大きい別のサンプル材料を使用してプロットを再作成してみましょう. その結果, 下図のような応答が得られます. 周期に対する電圧と電流の遅れはごくわずかで, 容量性効果がほとんどないことを意味します. あるいは, システムインピーダンスはほぼ純粋な抵抗性で, 対象周波数範囲にわたって一定です. 同様に, 同じ波形形状を使用しても, 10倍遅ければ, 応答は同じようになります.
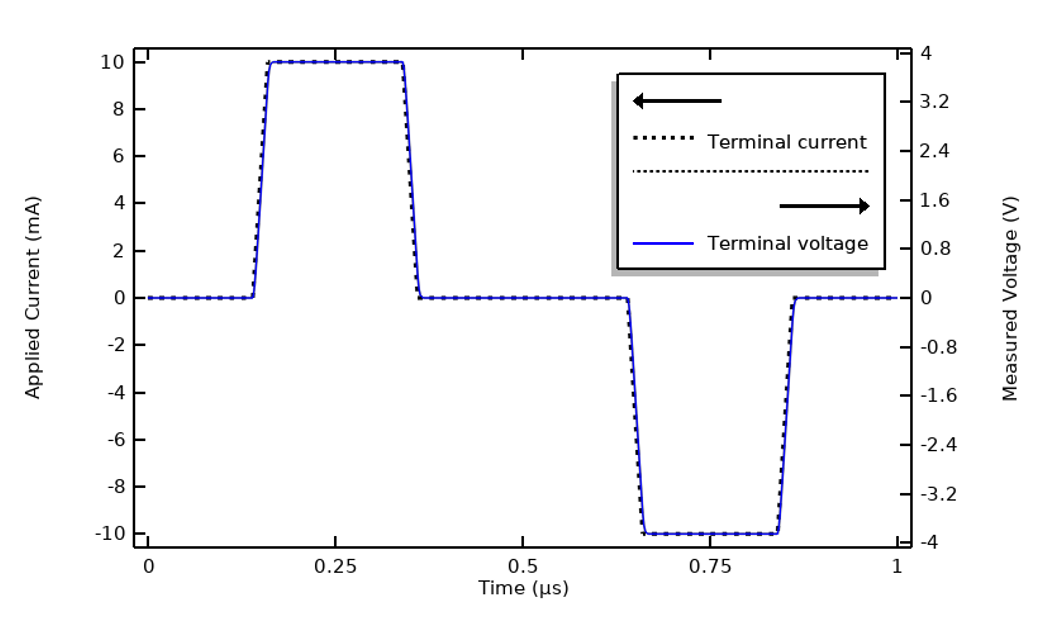
電気伝導率を10倍に変えると, システムの応答が変わります. 容量効果は無視できるほど小さくなります.
ほぼ純粋な抵抗系を扱っていると仮定し, 加えられた信号の周波数成分に関して電気伝導率が一定であるという仮定の下では, 電気モデルを定常 DC 問題まで単純化することができ, したがって, 容量効果とその結果生じる変位電流を完全に無視することができます. 次に,電流フィジックスインターフェースを定常形式で解くことができ, 適用される DC 信号は, 過渡信号の2乗のサイクル平均の平方根になります.
この式は, 励起が電流, 電圧, 終端電圧のいずれであっても同じです. 電気特性が周波数と電場強度に関して一定である限り, この単純化を使用することは有効です.
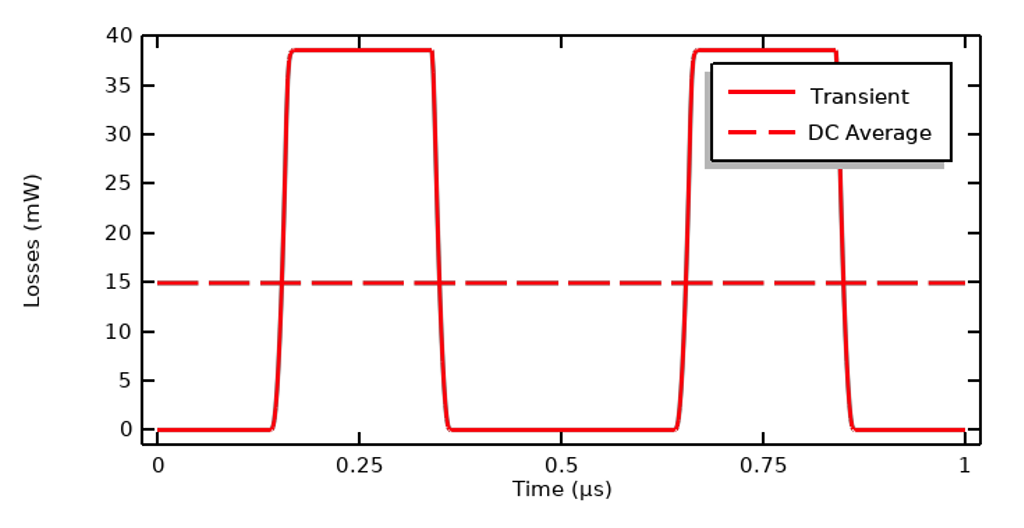
ほぼ純粋な抵抗体の時間領域損失と直流等価平均.
おわりに
これまで, 周期的な電気的励振をモデル化する方法と, 単一周期でそれを考慮する方法について見てきました. 入力信号の FFT を取ることによって, 重要な周波数成分を特定することができ, 過渡系応答は, 一連の周波数に対する解法と IFFT スタディステップの組み合わせによって予測することができます.
この FFT と IFFT の結果は, 経時的な応答を予測するために使用することができ, 電熱加熱シミュレーションの入力として使用することができます. 周期的な信号をいくつかの高調波の和として近似することは特に効率的であり, これによって双方向に連成したマルチフィジックス問題として非常に効率的に扱うことができます. 問題の種類によっては, 周波数成分を完全に無視することで, さらに単純化することができます.
この分野でモデリングを行っている場合は, マルチフィジックスモデルを構築する際に, これらの複雑さと単純化のすべてを十分に認識する必要があります.





コメント (0)