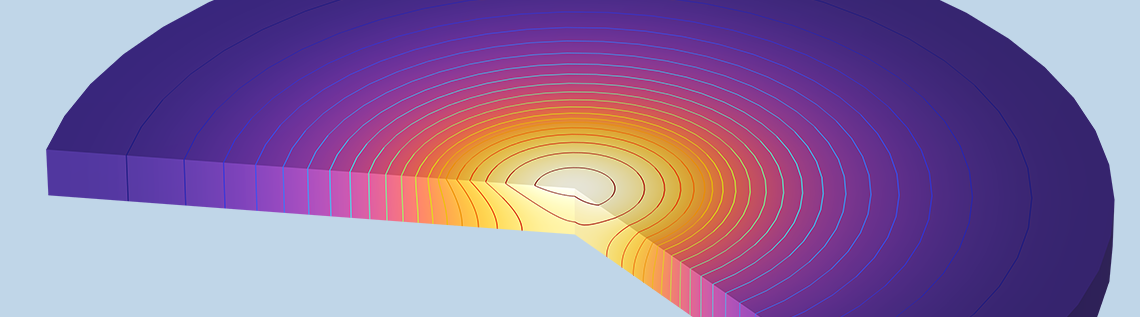
COMSOL Multiphysics®ソフトウェアは, 固体の過渡加熱のモデリングによく使用されます. 過渡熱伝達モデルは設定も解法も簡単ですが, 扱いが難しい場合もあります. 例えば, 結果の解釈は, COMSOL® の上級ユーザーさえ混乱させることがあります. このブログでは, 単純な過渡加熱問題のモデルを見ていき, これらのニュアンスを深く理解できるようにします.
単純な過渡加熱問題
図1は, このブログのテーマであるモデリングシナリオを示しています. このシナリオでは, 均一な初期温度を持つ円柱材料の先端表面の円形領域に, 空間的に均一な熱負荷が加えられます. 負荷の大きさは, 最初は高いが, しばらくすると段階的に小さくなります. この熱負荷に加えて, 上面全体からの熱放射をモデル化する境界条件が含まれ, これにより部品が冷却されます. 材料特性 (熱伝導率, 密度, 比熱) と表面放射率は, 想定される温度範囲において一定であると仮定します. また, 他の物理的な現象は発生しないものとします. このモデルの目的は, 時間経過に伴う材料内の温度分布を計算できるようにすることです.
同様のモデリングシナリオが, チュートリアルモデル “シリコンウェハーのレーザー加熱” でも紹介されていますが, ここで説明する内容は, 過渡加熱を伴うあらゆるケースに適用できることに留意してください.
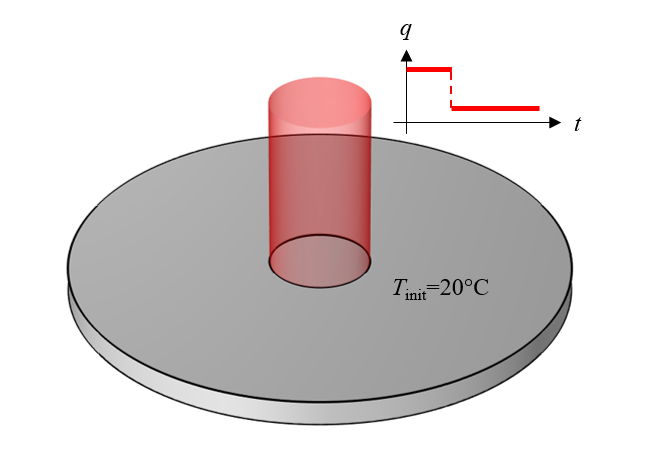
図1. 上面に熱源のある円柱状の材料.
図1に示されている正確なジオメトリを描くことからモデルの設定を始めたくなりますが, ここではより単純なモデルから始めることにします. 図1では, ジオメトリと荷重が中心線に対して軸対称であることがわかるので, 解も軸対称になることが合理的に推測できます. したがって, モデルを2D軸対称モデリング平面に簡略化することができます. (対称性を使ってモデルサイズを小さくする方法の概要をこちら からご参照ください.)
熱流束は中央の円形領域にわたって均一です. これをモデル化する最も簡単な方法は, 2Dドメインの境界に点を導入してジオメトリを変更することです. この点は境界を加熱部分と非加熱部分に分割します. この点をジオメトリに追加することで, 結果として得られるメッシュが熱流束のこの変化に対して正確に一致するようになります. これらのことを念頭に置いて, 2D軸対称で3Dモデルと同等な計算モデル (図2) を作成することができます.
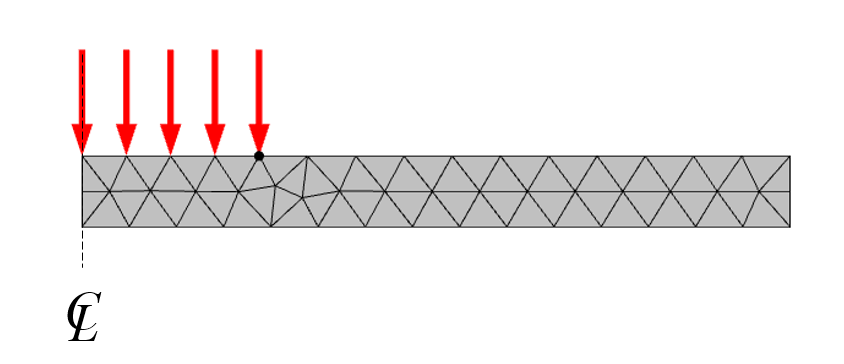
図2. 3Dモデルと同等の2D軸対称モデル. デフォルトのメッシュで表示されています.
今回検討しているケースは, 適用される熱流束の大きさの瞬間的な変化も含んでいます. t = 0.25 秒で, 熱流束は低い値に下がります. このような負荷のステップ変化には, 荷重の時間的なステップ変化を伴うモデルの解法についてのナレッジベースの項目にあるように, イベントインターフェースを使用する必要があります. 要するに, イベントインターフェースは, 荷重の変化がいつ発生するかを正確にソルバーに伝え, ソルバーはそれに応じて時間ステップを調整します. また, ソルバーがどの時間ステップを実行しているかを知ることも必要です. ソルバーが実行しているステップで結果を出力するようにソルバーの設定を変更し, 図3に示すように, 部品の上部中央にある点の温度をプロットすることもできます.
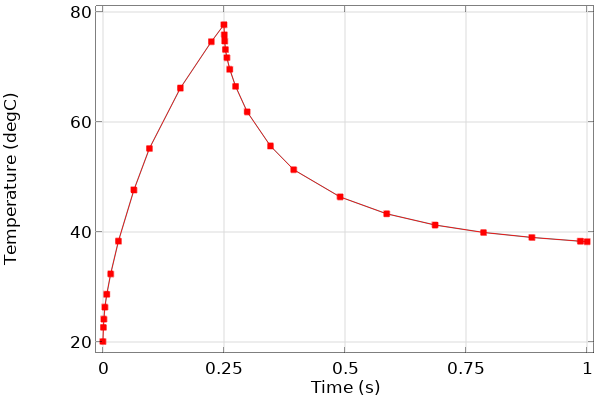
図3. ある場所での時間経過に伴う温度のプロット. 負荷の急激な変化の近くでは, ソルバーが実行するステップが短くなっていることを示しています.
次に, ソルバーの相対許容値を変えてモデルを再実行し, プロットで比較します (図4). このようなプロットは, 予想通り, 許容値をきつくすると解は急速に同じ値に収束していくことを示しています.
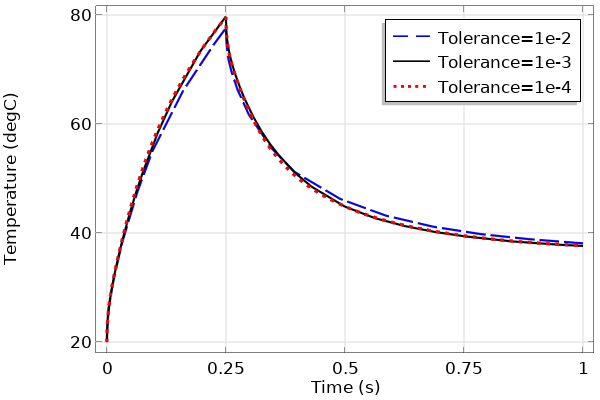
図4. 相対許容値を変えて解いた, ある点における温度の経時変化のプロット.
ここで評価できるもう一つの量は, ドメインに入るエネルギーの総量です. 全熱流束の式 ht.ntefluxを境界上で積分し, timeint()演算子を使って時間積分することで, 総エネルギーを得ることができます. この積分の結果を, 時間ステップの相対許容値の増加について, 以下に示しています. (ヒント: 空間積分と時間積分の計算については, こちらのナレッジベース項目をご覧ください. また, エネルギー収支の計算については, 質量保存とエネルギー収支の計算方法についてのこちらのブログをご覧ください.)
| ソルバー相対許容値 | モデリングドメインへのフラックスの時間積分 (J) |
|---|---|
| 1e-2 | 32.495 |
| 1e-3 | 32.469 |
| 1e-4 | 32.463 |
このデータからわかるのは, システムに入る総エネルギーは, 実は時間ステップの許容値にほとんど依存しないということです. 一見すると, これは私たちのモデルを素晴らしく検証してくれているように思えます. しかし, ここで私たちが観察しているのは, 有限要素法(FEM)の基本的な数学的特性なのです. 要するに, 総エネルギーは常に非常によくバランスが取れているのです. これは, モデルに誤差がないという意味ではなく, 誤差が現れる場所が違うということを意味します. それでは, 誤差を探してみましょう.
発生しやすいが, 定義が難しい誤差
ここで一旦立ち止まり, 上の段落にある誤差という単語を細心の注意を払って取り上げる必要があります. “誤差”という言葉は, モデリングとシミュレーションの世界では, しばしば脈絡なく, また十分な正確さを欠いたまま使われます. このセクションの残りの部分では, 様々なモデリングのケースで現れる可能性のある様々な誤差について, 詳細に説明します. (モデルの誤差に関するセクションに進みたい場合は, こちらをクリックしてください.)
入力誤差
入力誤差とは, その名の通りモデルの入力に誤りがあることで, 例えば材料特性が正しく入力されていなかったり, ジオメトリの描画が間違っていたりすることを指します. 最も厄介な入力誤差の一つは, 境界条件の入力忘れなどの入力漏れ誤差です. 入力誤差は, 入力の不確実性とは異なります. 例えば, 正確な材料特性がわからない場合に発生します. 前者は注意深い簿記によってのみ対処できますが, 後者は不確実性定量化モジュールによって対処できます. この例では, 入力誤差や不確実性はないものとします.
ジオメトリ離散化誤差
ジオメトリ離散化誤差は, 有限要素メッシュを介してジオメトリを離散化するとき, 特に非平面境界をメッシュ化する場合に発生します. これらの誤差は, メッシュの微細化が進むにつれて減少し, 実際に有限要素モデルを解くことなく評価することができます. 私たちの2D軸対称モデリングドメインには曲がった境界がないため, この種の誤差についても心配する必要はありません.
解の離散化誤差
解の離散化誤差とは, 有限要素の基底関数が, このドメイン内の真の解とその微分を完全に表現できないという事実の結果です. これは有限要素法の中に根本的に存在するものです. ジオメトリ離散化誤差と本質的に関連しているこの誤差は常に存在し, 適切に解かれた有限要素問題であれば, メッシュの細分化によって常に減少します.
時間ステップ誤差
時間領域モデルにおける誤差伝播を理解することは, かなり複雑です. このブログでは, ある時間ステップで導入された, あるいはすでに存在している誤差は前方へ伝播していきますが, ここで取り上げるタイプの拡散問題では, それらは減衰していく, という理解で十分です. この種の誤差は常に存在し, その大きさは時間依存ソルバーの許容値とメッシュの両方によって制御されます.
解釈誤差
もう一つのエラータイプは, より定性的な“解釈誤差”です. これらの誤差は, 結果の意味とその生成方法が正確に理解されていない場合に発生します. 最も有名なものに, 鋭角部での特異点があり, これは構造力学や電磁場モデリングでしばしば発生します. 解釈誤差は, 入力誤差が存在する場合に特によく発生します. 従って, 結果に確信が持てない場合は, モデルへのすべての入力をさかのぼってダブルチェック (あるいはトリプルチェック!) することが重要です.
誤差の種類はこれだけではありません. 例えば, 線形システムソルバー, 非線形システムソルバーの有限精度演算による数値誤差, および数値積分誤差などもあります. しかし, これらや他の種類の誤差は, 常にはるかに小さいものです.
以上の定義が終わったところで, モデルに戻る準備が整いました.
空間と時間の誤差の追跡
これまでのところ, モデルの特定の点での解を見て, 時間依存ソルバーの相対許容値を狭めると, 解が非常によく収束することを観察してきました. したがって, 時間依存ソルバーの相対許容値を狭めると, 時間ステップの誤差が減少するという考え方は, すでに理解できました. 次に空間温度分布を見てみましょう. まず中心線に沿った温度から始め, 最も緩い許容値1e-2で, ソルバーが取った最初の時間ステップと初期時間の解を見てみましょう.
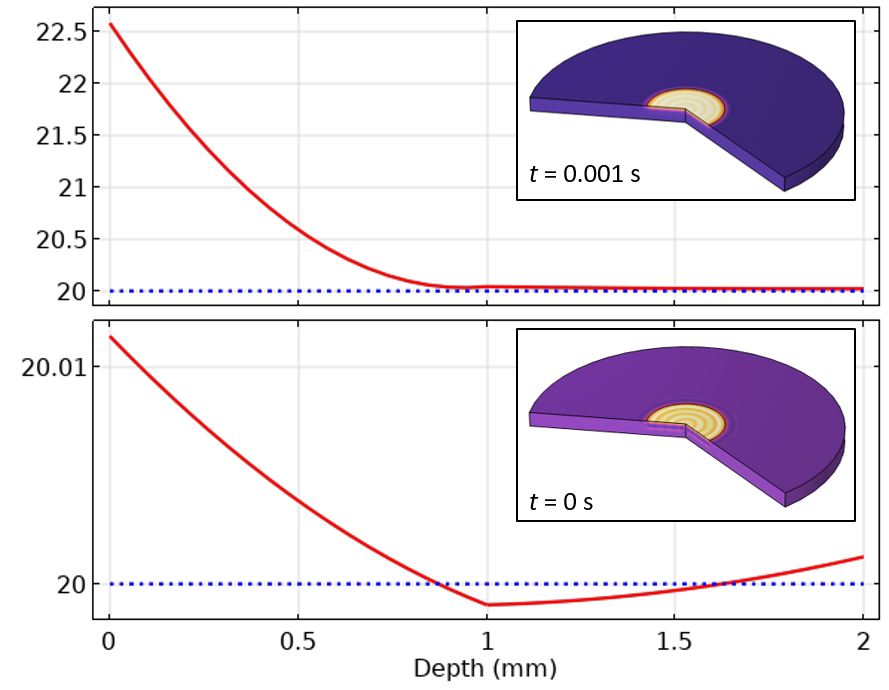
図5. 初期時間と最初の時間ステップにおける中心線温度のプロット.
初期値プロットから, 中心線に沿った温度は指定された初期温度と一致せず, 初期値よりも低い場所さえあることがわかります. これは, COMSOL Multiphysics® が, 初期時間における解の場を境界条件と初期値とが一致するように調整する, いわゆる整合的初期化を使用しているためです. 整合的初期化では, ゼロ時間上に発生すると考えられる非常に小さな人工的な時間ステップを追加で取る必要があります. 整合的な初期化は, 初期時間ステップのソルバー設定内, もしくは明示的なイベントおよび暗黙的なイベント機能でオフにすることができますが, これには注意が必要です. より一般的なマルチフィジックスモデル, 特に流体流れを含むモデルでは, デフォルトで有効にしておいた方がよりロバスト性が高くなる場合があります. ここではそのような例について説明します.
ここでは, 整合的初期化とは, 温度場を適用荷重と境界条件に一致するように調整するものであると考えます. 適用される熱負荷は初期状態では非ゼロなので, 熱流束に比例する温度場の勾配も初期状態ではゼロでなければなりません. また, この場は有限要素の基底関数を用いて離散化されることを考慮する必要があります. 中心線に沿って, これらの基底関数は多項式ですが, 多項式を真の解に正確に一致させることはできません. したがって, 整合的初期化ステップの後に得られる解は, 期待される結果をわずかにオーバーシュートまたはアンダーシュートします. 最初の時間ステップの解から, 部品の反対側の温度がすでに上昇していることもわかりますが, これは想定外です. これらの想定外のことは, 大きさとしては非常に小さいですが, 最小限に抑えたいところです.
このような解の離散化誤差を減らすためにモデルを修正する前に, この問題に少し物理的な直観を適用してみましょう. シミュレーションの開始時, 中心線に沿った温度分布は, 一次元スラブを通る熱伝達のシミュレーションを含むモデリングシナリオの解とよく似ています. この種のモデリングシナリオについては, すでに解析解が存在し, 熱伝達解析に関する多くの書籍で取り上げられています. (実際, この例は私の机の上にある教科書, 熱と質量伝達の基礎の表紙に使われています.)
簡潔にするため, 解析的な解法は省略し, 結果だけを述べることにします. 表面部分に熱を加えると, 表面の温度は上昇し始め, やがて内部の領域も暖かくなります. 境界から離れた点ほど, 加熱に時間がかかることに注意してください. スラブ内部の温度は均一には変化しません. 内部の点では, 温度が変化し始めるまでには, スラブ表面に近い点と比較して, より時間がかかります. 空間的な温度変化は, 熱伝達方程式の拡散的な性質により, 時間の経過とともに滑らかになることに注意してください. このことを理解した上で, モデルに戻り, どのように改善するかを見てみましょう.
つまり, この解の離散化誤差を最小化するためには, 場が大きく変化する部分をより細かくメッシュ化する必要があるということです. 私たちの直感 (あるいは, 調べたい場合は解析解) に基づくと, 場は表面に非常に近く, 境界に垂直な方向で大きく変化しますが, 内部ではより滑らかになることがわかります. これはまさに, 図6に示すように, 境界に垂直な方向に薄い要素を作成する境界層メッシュを必要とするような状況です.
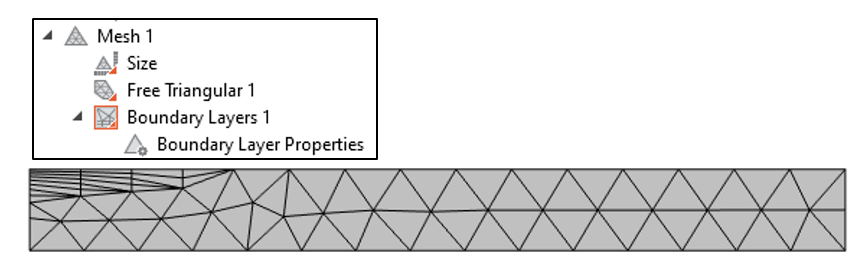
図6. ウェハー上面の1つの境界に沿って境界層を追加することで, メッシュシーケンスを変更しています.
これでシミュレーションを再実行し, 初期時間と次の時間ステップでの解をプロットすることができます.
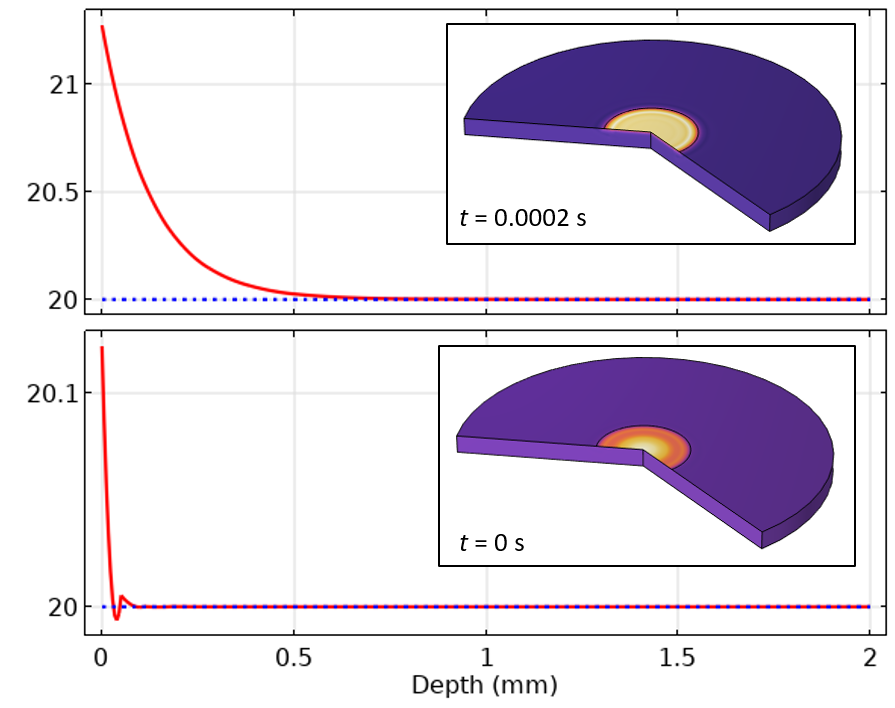
図7. 境界層メッシュを使用した場合の初期および最初の時間ステップにおける中心線温度のプロット.
図7を見ると, 初期値における温度のアンダーシュートが, 空間的にかなり局所的であることがわかります. より細かいメッシュを使用することで, 時間依存ソルバーの時間ステップも小さくなることがわかります. つまり, メッシュを細かくすることで, 空間離散化と時間ステップの両方の誤差を減らすことができたのです.
また, モデリングドメインの上部境界に沿った結果も見ることができ, これは露出した表面上の温度分布を表しています. 図8では, 許容値を1e-2として, 初期時間と最初の時間ステップについてプロットしています. これらのプロットでは, 空間的にかなり劇的な振動場が観察できます. これは空間離散化の兆候です. 熱負荷は半径軸に沿って大きさが段階的に変化することに留意してください. ここで観察されているのは, ギブス現象にやや似ています.
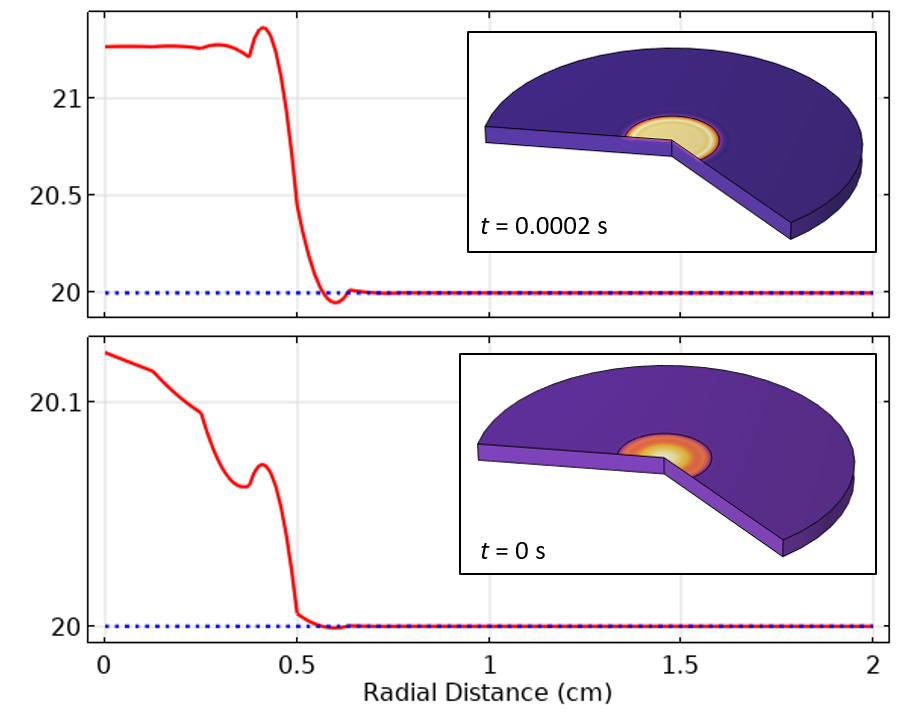
図8. 境界層メッシュを使用した, 初期値と最初の時間ステップにおける上面に沿った温度のプロット.
解法は以前と同様ですが, 今度は境界層との境の部分で局所的にメッシュを細かくする必要があります. この問題では, 描画点にもっと細かいサイズ設定を適用することが可能で, その結果, 下図のようなメッシュになります.
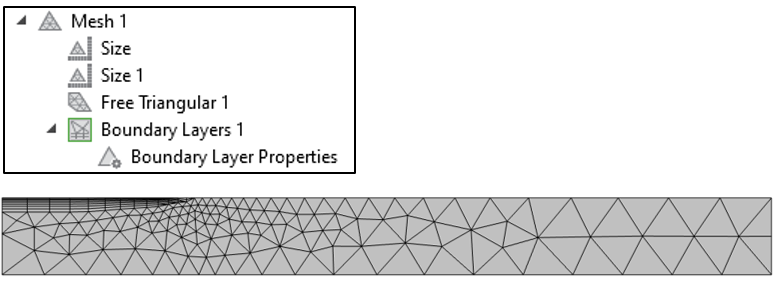
図9. メッシュ設定と メッシュ のプロット. 熱負荷分布を示す点では, 小さいメッシュサイズが適用されています.
図10の温度結果から, 解の振動が減少し, 空間的にも時間的にもあまり伝播していないことがわかります. ソルバーの相対許容値が1e-2であっても, 解はすでに大幅に改良されています.
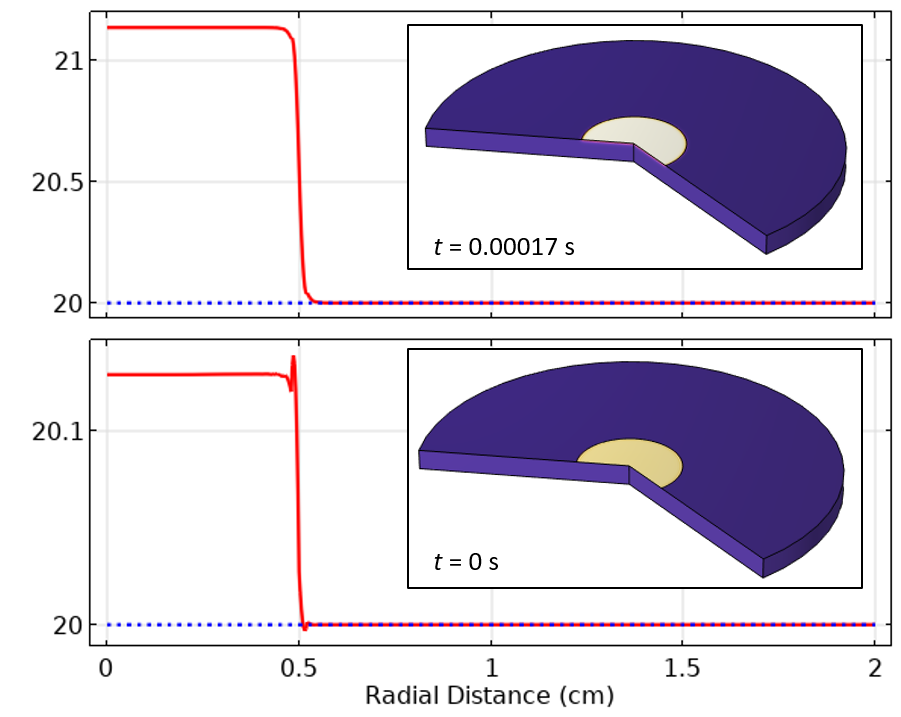
図10. メッシュを細分化し, 相対許容値を0.01にしたところ, 初期値と最初の時間ステップにおける上面に沿った温度はより正確になりました.
メッシュとソルバーの許容値をさらに細かくして, この演習を続けることも可能です. しかし, これまでに行った改良によって, 誤差が急速に減少し, まだ存在する誤差でさえも, 過渡熱伝達方程式の拡散的な性質により, 空間的にも時間的にも平滑化されることがすでにわかり始めています. 実際, 私たちはモデル入力の不確実性の影響を調べるのに, 同じくらいの労力を費やすべきでしょう.
それ以外には?
この例では, 境界全体にかかる熱負荷は時間的に移動しないため, 境界を分割するというアプローチが妥当です. 熱負荷分布が移動する場合は, 加熱面のメッシュ全体をより細かくする必要があります. (COMSOL ®で移動荷重と制約をモデル化する3つのアプローチについては, こちらを参照してください).
このブログの前半で, 材料特性は温度に対して一定であり, 他の物理特性には依存しないと仮定されていると述べました. すべての材料特性は温度によって変化するため, これは事実をかなり単純化したものです. 実際に, 材料は融解のような相変化を起こすことさえあります. 相変化は, 非線形の比熱を使用して相変化の潜熱を考慮する見掛けの熱容量法など, いくつかの異なる方法でモデル化することができます. また, 熱硬化の方程式を含むようなマルチフィジックス問題や, 材料非線形電磁加熱問題なども容易に想定できます. このような場合, 温度場だけでなく, 解かれる他のすべての場変数, そして場合によってはそれらの時間的空間的導関数の収束を観察する必要があります. このようなケースでは, モデリングドメインのあらゆる場所で非常に細かいメッシュが必要になるため, この単純な状況からの教訓は生かされません. しかし, はるかに複雑なモデルをメッシュ分割して解く場合でも, 可能な限り単純なケースを常に念頭に置いておくことをお勧めします (たとえそれが概念的な出発点にしかならないとしても).
加えて, このブログは固体材料の時間変化する加熱についてのみ取り上げていることを強調しておきます. 流体が移動している場合には, 支配方程式は大きく変化します. 流体フローモデルのメッシュ分割は, 別の比較的複雑なトピックです. 波動タイプの問題の場合, メッシュとソルバーの設定の選択は比較的単純になります.
おわりに
このブログでは, 典型的な熱伝達モデリング問題を取り上げました. 負荷が急激に変化すると, 空間と時間の両方で, 解にある種の誤差が生じることを確認しました. 読者の皆さんは, このような誤差がどのようなものかを理解し, 他の数値計算手法と同様, 現実の近似に過ぎない有限要素法の本質的な結果であることを理解できたはずです. これらの誤差は一見大きく見えますが, 過渡熱伝達方程式の拡散的性質により, その大きさは空間的にも時間的にも減少します. また, メッシュの細分化によって空間的な離散化誤差が減少し, これは暗黙的に時間ステップ誤差を減少させる効果があることを示しました. 最後に, ソルバーの相対許容値の精密化により, 時間ステップ誤差をさらに低減できることを説明しました.
さらに簡潔にまとめると, 比較的長い時間後の解に興味があるのであれば, かなり粗いメッシュとデフォルトのソルバー相対許容値を使用してもまったく問題ありません. 一方, 短時間での小規模な温度変化に興味がある場合は, ソルバー相対許容値とメッシュの精密化の両方を検討する必要があります.
これを理解することで, 解釈の誤りを避けることができます. これにより, 単純なモデルからより複雑なモデルを自信をもって簡単に構築できるようになります.
次のステップ
下のボタンをクリックしてアプリケーションギャラリにアクセスし, このブログで紹介しているモデルを試してください.



コメント (0)