
2D 軸対称固体力学インターフェースで, ねじれや曲げを解析できることをご存知ですか? バージョン 6.0 以降の COMSOL Multiphysics® ソフトウェアの機能により, 通常は完全な3D 解析を必要とする2D 軸対称のモデルを簡単に設定することができます. 拡張された定式化を使用すると, 例えば, 軸力によってねじれる異方性材料, ねじりによって負荷される円周方向の亀裂, または曲げに対する応力集中係数を, すべて 2D ジオメトリを操作しながら解析することができます. では, その仕組みを見ていきましょう.
2D 軸対称性とは?
前回のブログ“平面応力と平面ひずみの違いとは?”では, 3D 立体物の解析における, 平面外方向の応力やひずみフィールドを仮定し, 平面2D 近似を使用した解析について説明しました. 2次元軸対称も, 3D パーツを 2D ジオメトリに縮小する方法の一つです. 2D でのモデリングは, 完全な 3D モデルを構築するよりも計算量が少なく, また, 境界条件の適用やメッシュの作成が簡単に行えるという利点があります.
2D 軸対称で作業するには, ジオメトリ, および (通常, 常にではありませんが) 荷重と拘束がオブジェクトの円周上で一定であることが必要です. これらの要件が満たされていれば, 2D の断面だけを用いて運動方程式を定式化することが可能です. 2D スライスは, 全回転にわたって支配方程式を積分することにより, 完全な3D 応力状態およびひずみ状態を回復するのに十分です. 2D 軸対称解析の代表的な対象は, 圧力容器, スピーカーモジュール, 流体ミキサー, Oリング, シャフトなどです.
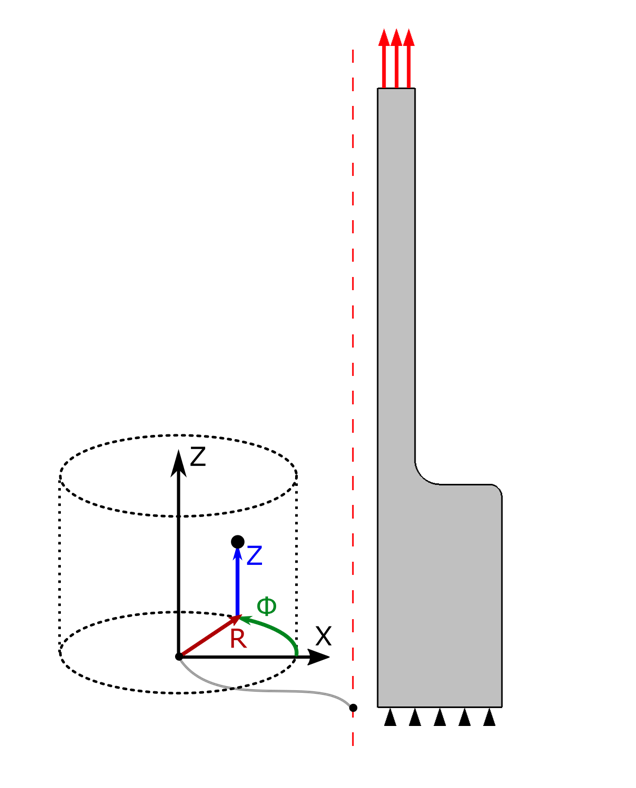
典型的な2次元軸対称解析. 3D シャフト(左), 上部に軸方向荷重が加えられた2D 軸対称ジオメトリ表現(中央), フォン・ミーゼス応力分布を示す復元された3D 解の断面(右).
デフォルトでは, 半径方向と軸方向の変位 u と w だけが2D 軸対称で求解されます. 円周方向成分 v はゼロと仮定されます. しかし, 2D 軸対称でねじれ変形を可能にする円周方向変位を含めることは可能です. この拡張機能を理解するために, まず, 一般的に変位勾配を用いて変形を記述する方法をおさらいしておきましょう. 次のセクションは, 内容について既に詳しい方は読み飛ばしてください.
変位勾配
固体力学インターフェースは, 運動方程式, つまりニュートンの第二法則を解きます. デフォルトの線形弾性材料ノードの方程式セクションには, 体積荷重で表現されたおなじみの質量×加速度=全体の力の合計と, この特定の材料モデルの特徴である応力とひずみの線形関係が表示されます.
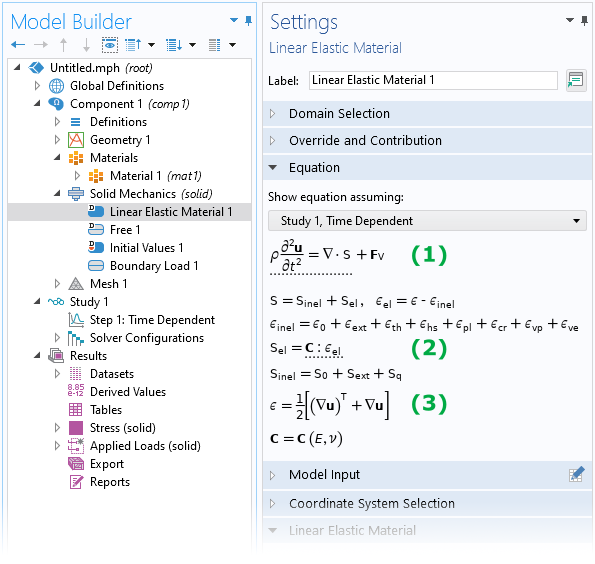
線形弾性材料ノードの方程式セクションには, 運動方程式 (1) と線形弾性構成方程式 (2), および工学的ひずみの定義(3)が表示されます.
連続体力学解析において構成関係を定式化するためには, 任意の点における材料の変形を何らかの適切な尺度で記述する必要があります. 実際, 工学ひずみ (上図 (3) ), グリーン・ラグランジュひずみ, 対数ひずみなど, 変形を特徴付ける指標は数多く存在します. これらの指標の有用性は, 特定の材料モデルを使用する場合や, モデルが大きな変形 (幾何学的非線形性) を含む場合など, コンテキストによって異なります. しかし, これらの指標はすべて変位勾配 \nabla \mathbf{u} (\textrm{grad} \, \mathbf{u}と表記されることもある) の関数として表現することができます.
しかし, 変位勾配とは何なのか, それはどこから来るのでしょうか? 大きな構造物の一部であるような, (限りなく) 小さな塊のような材料を考えてみましょう. 最初は, 時間 t_0 において, その小さな塊は基準形状 (下のグレーの面を参照) をしています. その後, ある時間 t で, 下のアニメーションのように, 剛体運動 (並進と回転) と変形 (伸張とせん断) が起こったかもしれません.
平面の2D 小さな塊が並進, 回転, 弾性変形 (純粋なせん断) している様子を, 個別の変形ステップとして可視化したもの. 変位勾配は, その小さな塊が変形した後に, \textrm{P}_1 と \textrm{P}_2のように最初は隣接していた2点間の変位の変化を表現するために使用されます.
アニメーションでは, \textrm{P}_1 と \textrm{P}_2 という2つの点がマークされています. これらは互いに限りなく近いと仮定しています. 初期状態では, 点 \textrm{P}_1 の位置は \mathbf{X} であり, 時間 t における現在の位置は \mathbf{x} と表記されます. 点 \textrm{P}_1 の新しい位置は, 元の位置に変位ベクトルを加えたもの, すなわち, \mathbf{x} = \mathbf{X} + \mathbf{u}(\mathbf{X}, t) と表現することもできます.
では, そのすぐ近くにある点 \textrm{P}_2 に注目してみましょう. 最初の点と同様に, \textrm{P}_2も時間 t 後に新しい位置に変位します. 唯一の違いは, 点 \textrm{P}_2 は \textrm{P}_1 から少し離れたところに位置していることです. つまり, その初期位置は \mathbf{X} + \textrm{d}\mathbf{X} と言うことです. したがって, その小さな塊が変形した後の \textrm{P}_2 の新しい位置は
この関係を少し整理すると, 変形後の点 \textrm{P}_1 と点 \textrm{P}_2 の間の小さなステップである \textrm{d}\mathbf{x} の式が得られます.
= \mathrm{d}\mathbf{X} + \mathrm{d}\mathbf{u} \\[1mm]
ここで, 変位勾配 \nabla \mathbf{u} とは, (初期配置における) 小さなステップ \textrm{d}\mathbf{X} を, 物体が変形したときの点 \textrm{P}_1 と \textrm{P}_2 間の変位変化に対応させるテンソルとして定義されます. 密接に関連する式として, I + \nabla \mathbf{u} = \textrm{d}\mathbf{x}/\textrm{d}\mathbf{X} を変形勾配 (F で示されることが多い)と呼び, 連続体力学の本にも多く登場する指標です.
簡単に言うと, \nabla \mathbf{u} は変位場\mathbf{u} = (u, v, w)^\textrm{T} の初期配置 (材料座標系も) に対する導関数を含むテンソルです. 3D 直交座標系では, 変位勾配は単純に次のようになります.
\left[
{\begin{array}{ccc}
\frac{\partial u}{\partial X} & \frac{\partial u}{\partial Y} & \frac{\partial u}{\partial Z} \\
\frac{\partial v}{\partial X} & \frac{\partial v}{\partial Y} & \frac{\partial v}{\partial Z} \\
\frac{\partial w}{\partial X} & \frac{\partial w}{\partial Y} & \frac{\partial w}{\partial Z} \\
\end{array} }
\right]
2D 軸対称の場合, 円筒系が使われ, その場合, 変位勾配は次のように定義されます.
\left[
{\begin{array}{ccc}
\frac{\partial u}{\partial R} & \frac{1}{R} \frac{\partial u}{\partial \Phi}-\frac{v}{R} & \frac{\partial u}{\partial Z} \\
\frac{\partial v}{\partial R} & \frac{1}{R} \frac{\partial v}{\partial \Phi}+\frac{u}{R} & \frac{\partial v}{\partial Z} \\
\frac{\partial w}{\partial R} & \frac{1}{R} \frac{\partial w}{\partial \Phi} & \frac{\partial w}{\partial Z} \\
\end{array} }
\right]
ここで, R, \Phi, Z はそれぞれ半径方向の座標, 円周方向の座標, 軸方向の座標です.
ひねりを加えて…
では, 変位勾配をどのように再定義すれば, 単純な2D 解析から2.5D 解析と呼ばれるような解析に拡張できるのでしょうか?
デフォルトでは, 2D 軸対称固体の円周方向の変位はゼロと仮定されます. これは, 半径方向と軸方向の変位のみを含むユースケースが多く, 変位成分 v を従属変数のリストに追加することで, 一定の計算コストがかかるためです. したがって, 2D 軸対称でねじれを解析するためには, 円周方向の変位を明示的に追加する必要があるのです. これは, 固体力学インターフェースの設定ウィンドウにある円周方向の変位を含めるチェックボックスを使用することで簡単に行うことができます.
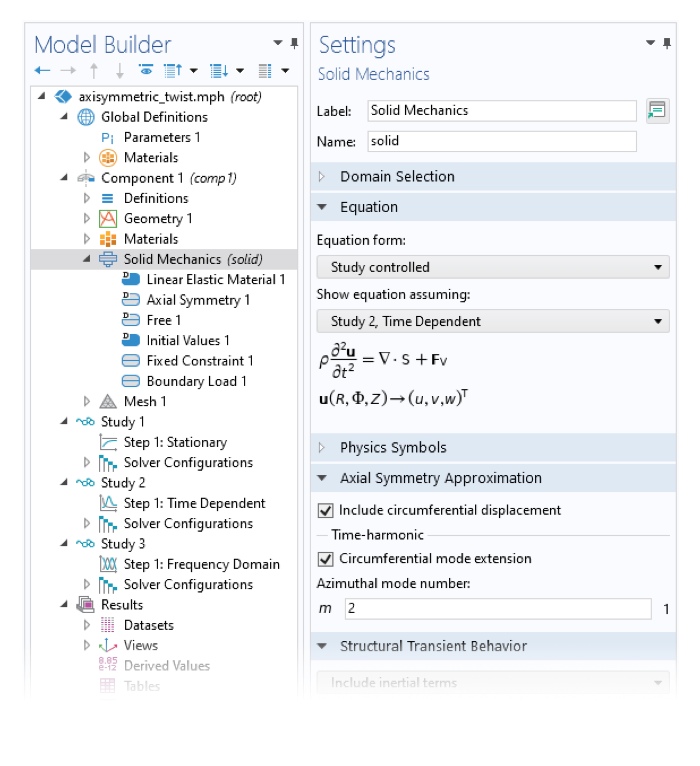
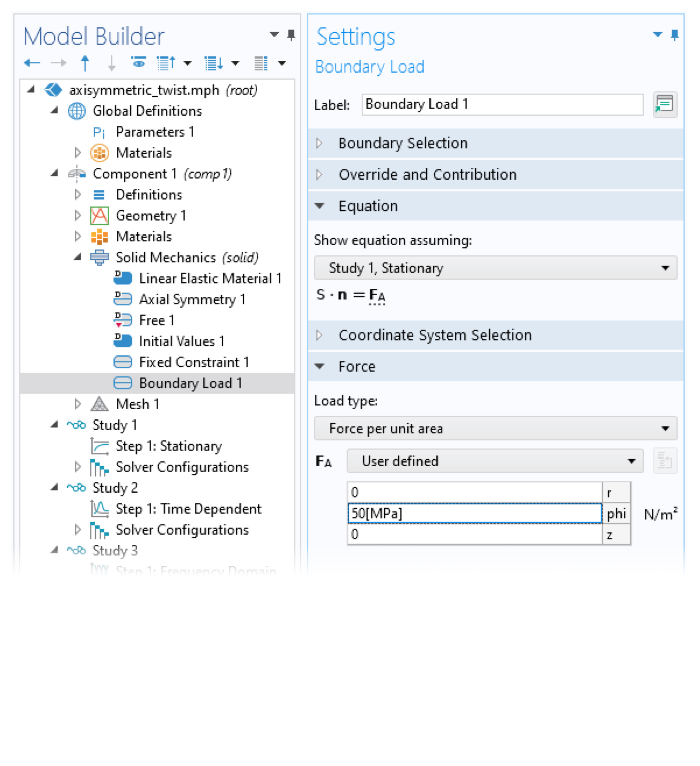
軸対称近似のチェックボックスを使用すると, 2D 軸対称モデルでの円周方向の変位が有効になります(左). 円周方向の変位を含めるチェックボックスを選択すると, モデルビルダーの多くのノードに, 方位角方向の荷重を適用する場など, ユーザー入力項目が追加表示されます (右).
円周方向の変位を含めるチェックボックスを選択すると, 3つの重要なことが行われます:
- 円周方向変位成分 v が新たな従属変数として追加される
- 円周方向に荷重, バネ, ダンパーを加えるなどの新しいユーザー入力が表示される
- 変位勾配の定義を変更する
最後のステップでは, 一般的な2D 軸対称解析ではゼロと仮定される平面外方向のせん断ひずみ (すなわち, \varepsilon_{R\Phi}と \varepsilon_{\Phi{Z}}) を求解することができるようになります. 唯一の制限は, 変位場がオブジェクトの円周上で一定でなければならないことです. 言い換えれば, \Phi に関する導関数はゼロ (\partial (…)/\partial \Phi=0) と仮定されます. したがって, 再定義された変位勾配は次のようになります.
\left[
{\begin{array}{ccc}
\frac{\partial u}{\partial R} & -\frac{v}{R} & \frac{\partial u}{\partial Z} \\
\frac{\partial v}{\partial R} & \frac{u}{R} & \frac{\partial v}{\partial Z} \\
\frac{\partial w}{\partial R} & 0 & \frac{\partial w}{\partial Z} \\
\end{array} }
\right]
ここで, v を含むすべての項は, 標準的な2D 軸対称の場合, 通常無視されます. ここで紹介している拡張機能は, すべてのスタディタイプで利用可能です.
円周方向の変位を含めることで, 通常は完全な3D 解析が必要なケースを解析することができます. 以下に, そのような例を2つ紹介します. 最初の例は, 不均衡なレイアップを備えた繊維複合材料などの異方性材料で作られたチューブを示しています. この場合, 弾性マトリックスにカップリング項が含まれているため, 軸方向に引っ張るとチューブがねじれるという現象が発生します. 2つ目の例は, 円周方向に亀裂が入った容器を示しています. 容器には内圧と周方向の力が加わっており, その結果, 亀裂には開口モードと面外せん断モードの両方が作用しています.
一般的に完全な3D モデルを必要とする解析の例: 材料特性による引張, 捻り結合が見られるチューブの正規化周方向変位 (左), 開口モードと面外せん断モードで亀裂を負荷した厚肉容器のフォン・ミーゼス応力分布 (右).
円周モード拡張
前述の \Phi 方向に一定の変位しか許容しないという制限は, 固有周波数解析や周波数ドメイン解析では若干解除することができます. ねじり振動のような問題では, 解が円周上に特定の周期性を持っていると仮定することが合理的です.この考え方は, 以下のように, 変位の複素数値の仮説で簡便に表現できます:
これは線形応答を仮定した有効な解であり, 周波数ドメイン解析ではとにかく最も一般的な基礎的仮定です. 上記で, m は変位場の周期数を定義する方位角モード番号です. この仮説では, 変位勾配は次のようになります.
\begin{bmatrix}
\frac{\partial u}{\partial R}&-\frac{v}{R}& \frac{\partial u}{\partial Z} \\
\frac{\partial v}{\partial R} &\frac{u}{R}& \frac{\partial v}{\partial Z} \\
\frac{\partial w}{\partial R}&0& \frac{\partial w}{\partial Z} \end{bmatrix} – i \frac{m}{R} \begin{bmatrix}
0 & u & 0 \\
0 & v & 0 \\
0 & w & 0
\end{bmatrix}
このタイプの2D軸対称拡張は, 円周モード拡張とも呼ばれ, 軸対称近似セクションの2番目のチェックボックスで有効にすることができます (上のスクリーンショット参照). モード番号はユーザー入力で指定する必要があります.
注目すべき特殊なケースは2つあります:
- m=0, (一定の v の変位に対応)
- m=1, (2D 軸対称の曲げ変形を表現)
なお, COMSOL Multiphysics では, 曲げ変形が許容されるように, 対称線における軸対称条件 (u=v=0) が自動的に変更されます.
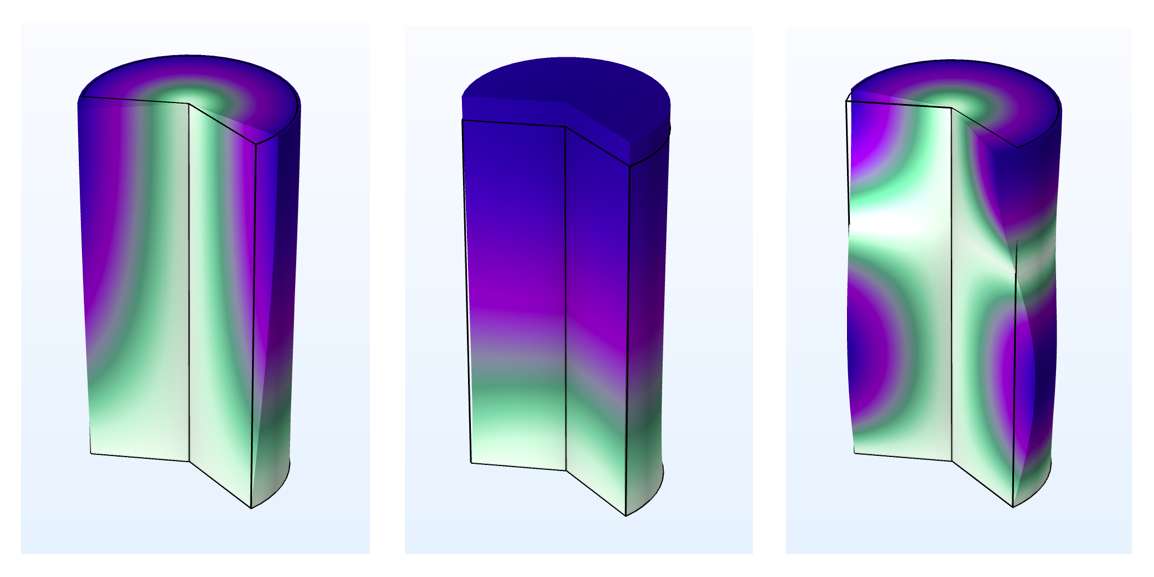
下図は, 円周モード拡張を使用して調べることができる固有モードの例を示しています. モード番号を変えることで, 軸対称の仮定が成立していれば, 対応する完全な3D 解析で見られるすべての固有モードを求めることができます.
| m=0 |
|
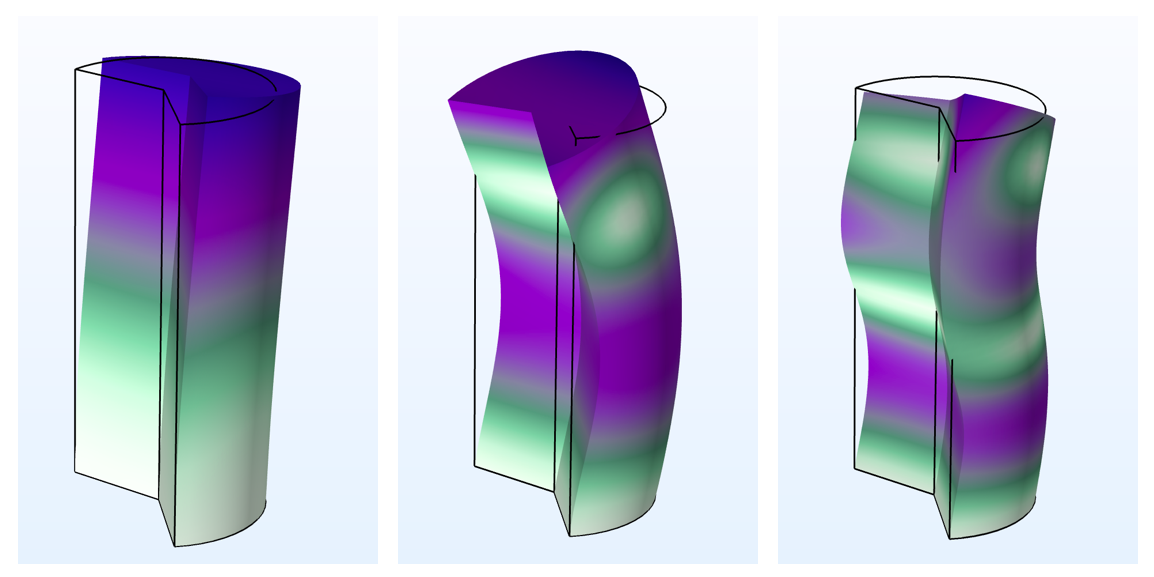
| m=1 |
|
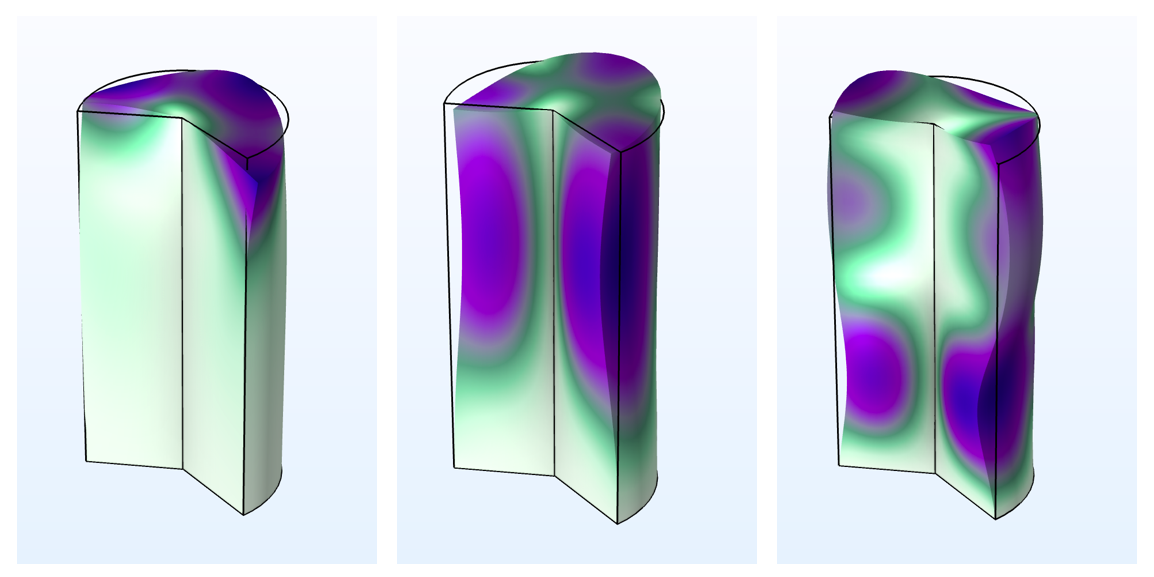
| m=2 |
|
円柱の最初の3つの固有モード. 一方の端が異なるモード番号 m に固定されています. この例では, m=0 はねじれモードと軸方向モードをもたらし, m=1 は曲げモードのみを生成し, m=2は高次のねじれモードを示します.
一般に,円周モードの拡張は,固有周波数や周波数ドメインのスタディにおいてのみ使用することができます. 定常および時間依存のスタディでは,周方向変位 v は一定となり, モード番号 m=0 に対応します. しかし, 周波数を 0\,\textrm{Hz} にして周波数ドメイン解析を行うと, すべての慣性項がゼロになり, すべての荷重が周波数に依存しなくなるため, 定常解が得られます. この方法を用いると, 2D 軸対称の静的曲げ変形を計算することができます. 下図は, シャフトに曲げ力 (モード番号 m=1) が加わり, 軸応力 \sigma_z を, シャフトの薄い部分と厚い部分の間の遷移領域で解析的に予想される応力と比較した例です.
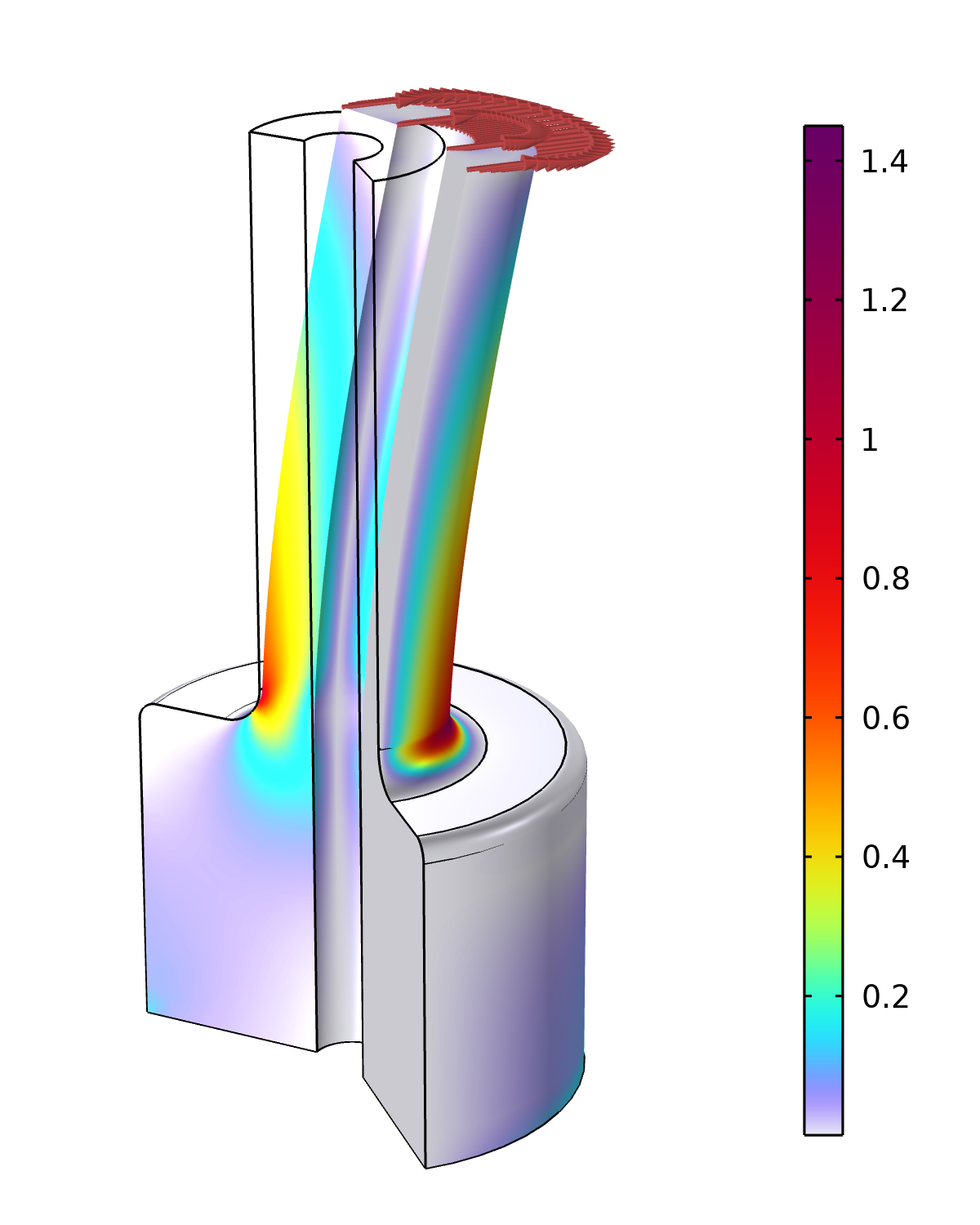
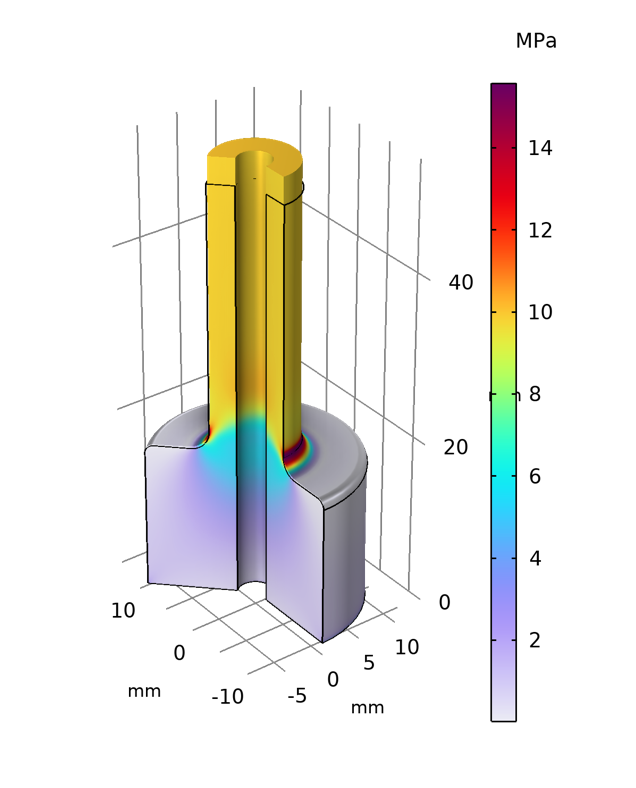
2D 軸対称でモデル化された曲げ力を受けるシャフト. このプロットは, 応力集中係数, より正確には, 初等曲げ理論から得られたフィレットドメインにおける実際の応力と予想される法線応力 \sigma_z の比を示しています.
このモデルへのリンク (この場合の荷重の適用方法の詳細も含む) は, 以下にあります.
他の構造力学インターフェース
より複雑な変位場を解くために, 2D の定式化を面外の自由度で拡張するという一般的な考え方は, 決して特殊なものではありません. 例えば, シェルインターフェースは, 円周モード拡張もサポートしています. そして, 固体力学インターフェースの平面2D に相当するものは, 面外モード拡張と呼ばれ, 2D固体力学設定ウィンドウで有効化できます. これにより, ユーザーは面外方向の波のような変位をモデル化することができます.
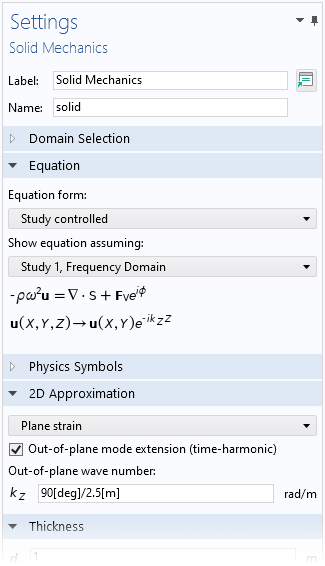
2D平面ひずみ定式化を用いた固体力学 の面外モード拡張 チェックボックス.
また, 他のフィジックスインターフェースでは, 同様のタイプの拡張機能を用いて, より高度な3D 場の求解をサポートしているものもあります. 例えば, 流体インターフェースでは, このオプションは旋回流と呼ばれます.
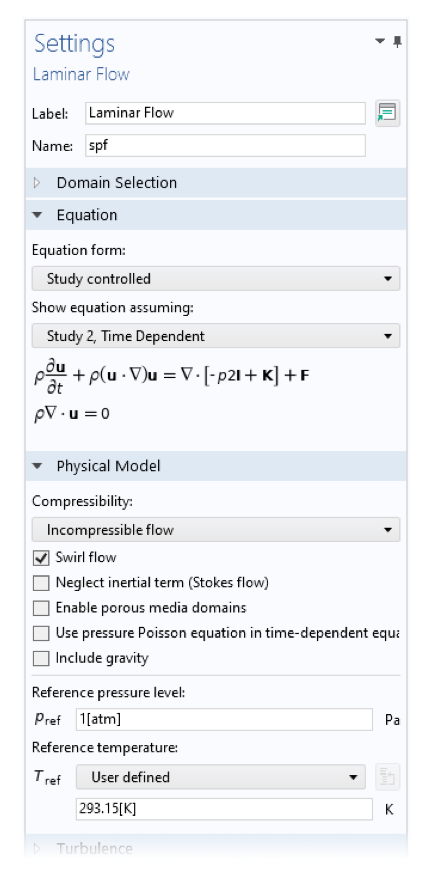
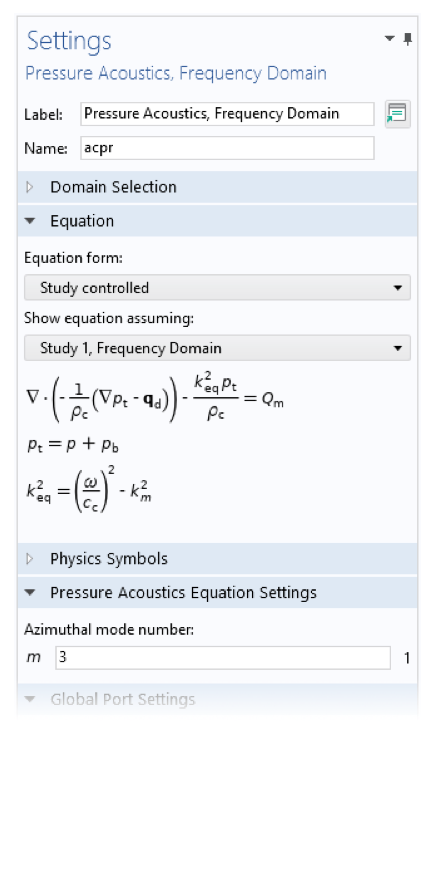
2D 軸対称の層流および圧力音響 (周波数領域)インターフェースの設定. 旋回流と方位モード数の設定により, 円周方向のより複雑な形状の場を解くことができます.
自分で試す
このブログ記事で紹介した2D 軸対称のねじれと曲げのモデリングを試してみませんか? 下のボタンをクリックして MPH-file にアクセスしてみてください.




コメント (0)