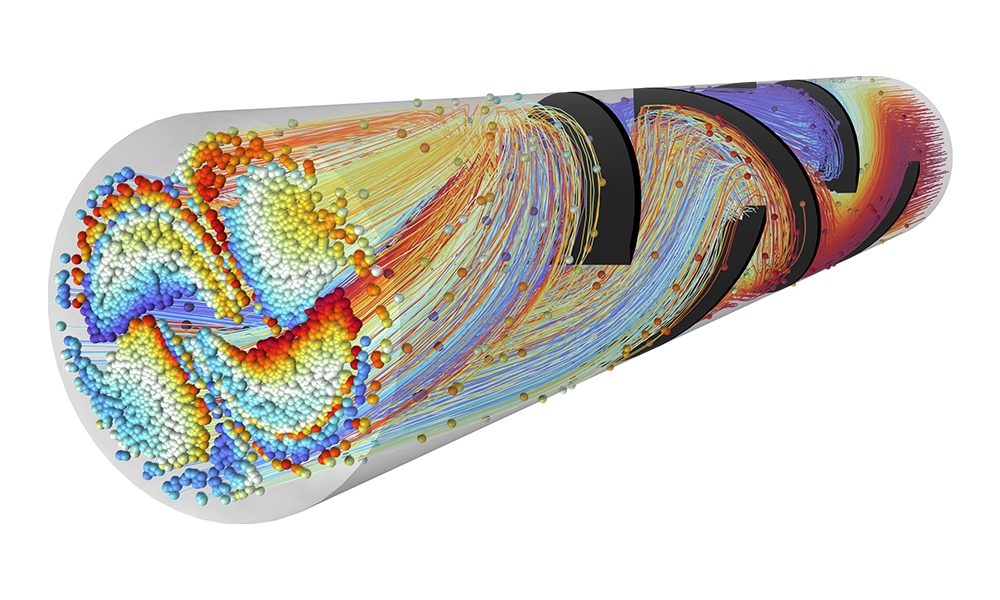
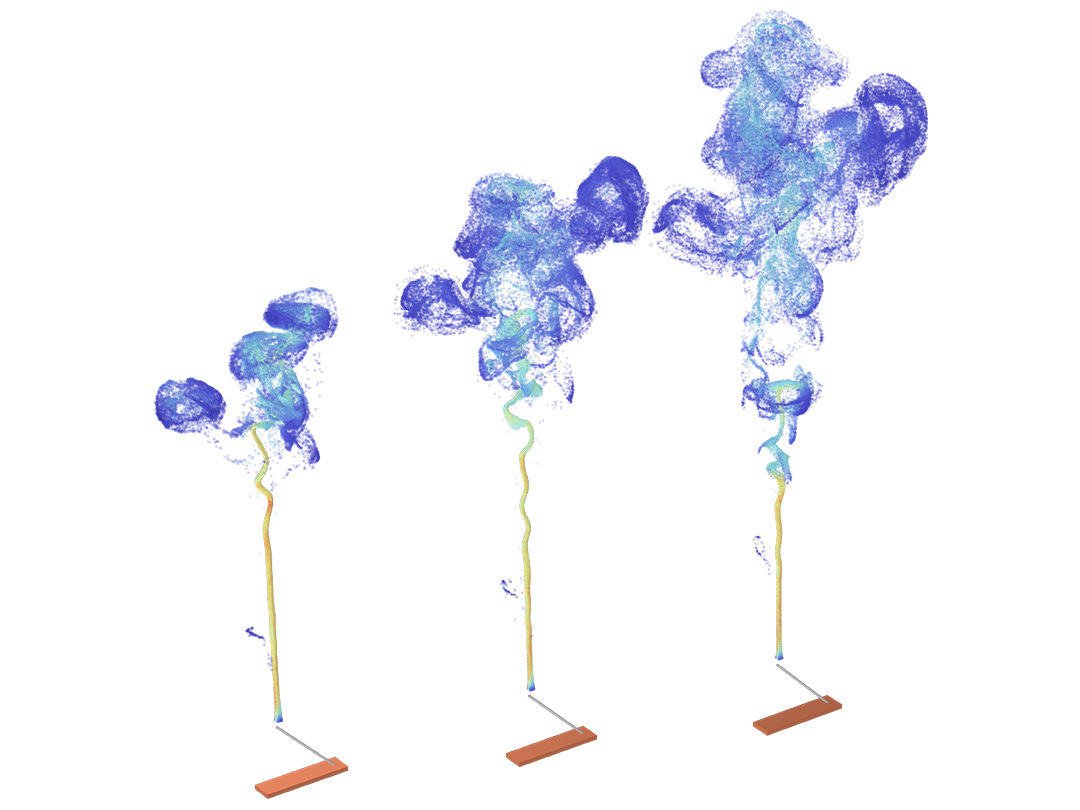荷電粒子追跡
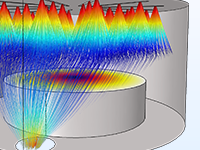
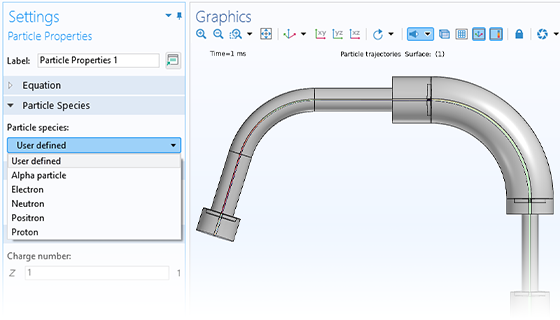
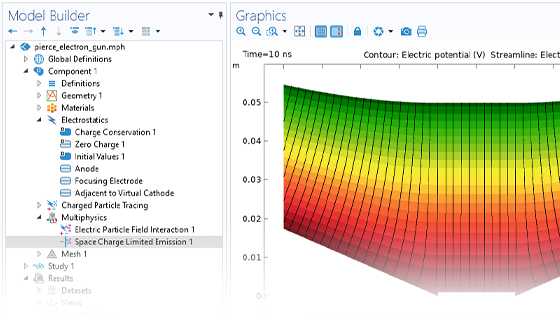
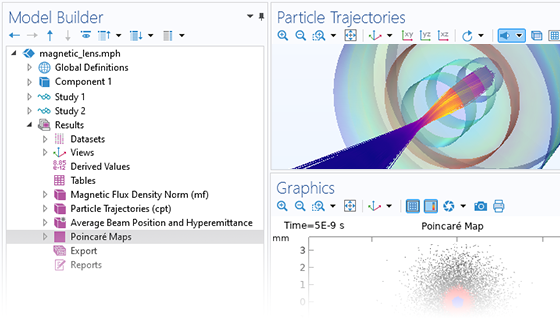
イオンや電子の動きを正確に予測することは, 分光器, 電子銃, 粒子加速器などの設計に欠かせません. 印加される場は, ユーザーが定義することもあれば, 過去の解析から取得することもできます. このような場は, 定常的であったり, 時間依存的であったり, 周波数領域で解いたりすることができます. 異なる場をいくつでも適用できるので, 同じシミュレーションの中で定常場と時間調和場を重ね合わせることができます.
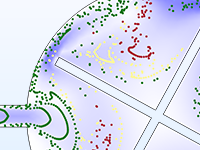
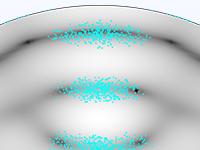
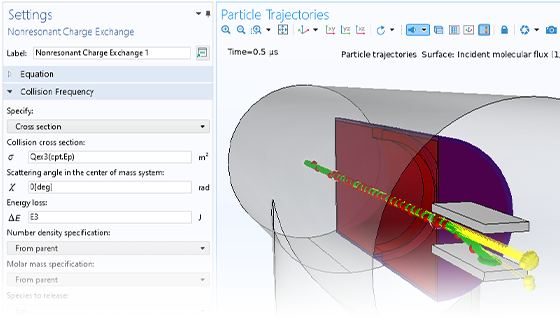
粒子の運動は, 完全な真空中で行われることはほとんどありません. 粒子追跡モデルをモンテカルロ衝突モデルに変換し, 粒子が周囲の気体中の分子と衝突する機会を与えることができます. これにより, 粒子は方向を変えたり, 電離や電荷交換などの反応を起こしたりすることがあります.
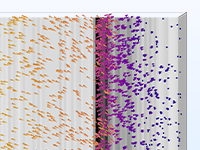
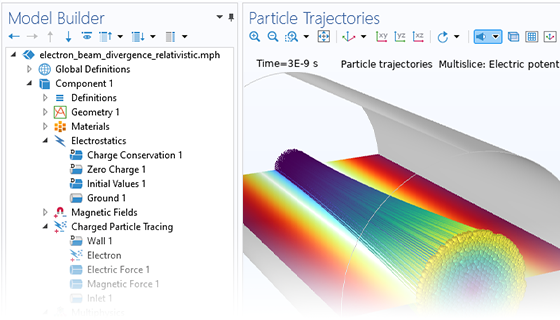
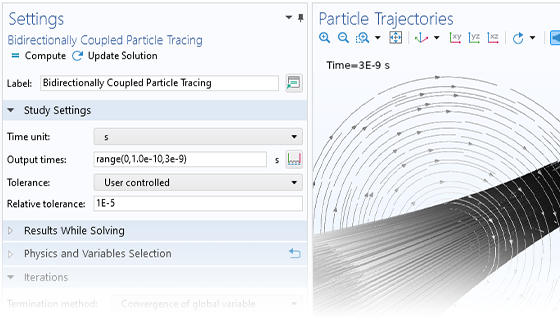
最も単純な荷電粒子追跡モデルでは, 一方向の 結合が行われ, 場が解かれた後, 粒子にかかる力を定義するために使用されます. 荷電粒子が十分に高い電流のビーム内にある場合, 粒子が場を乱すことができる双方向の結合を考慮する必要があるかもしれません. 双方向結合モデルを便利に設定するために, ビルトインされた解析タイプが利用できます.