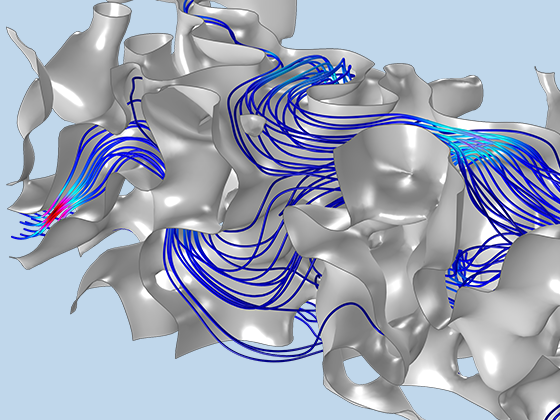
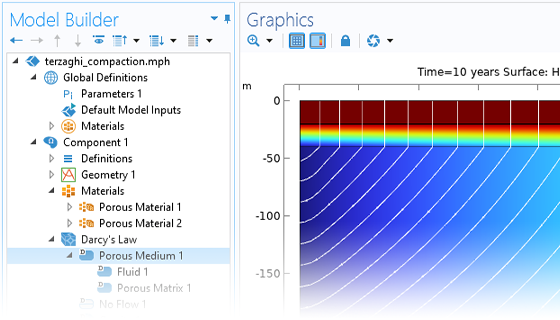
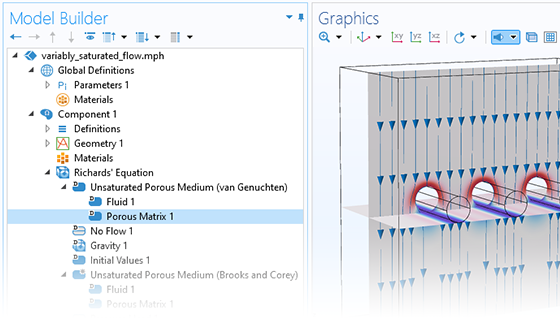
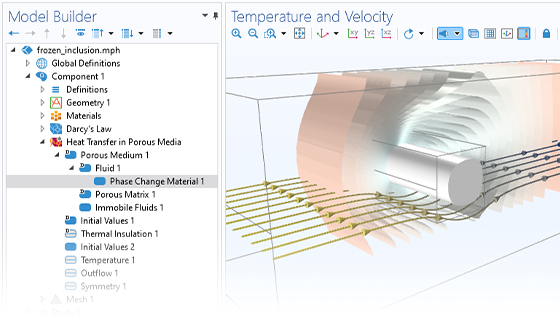
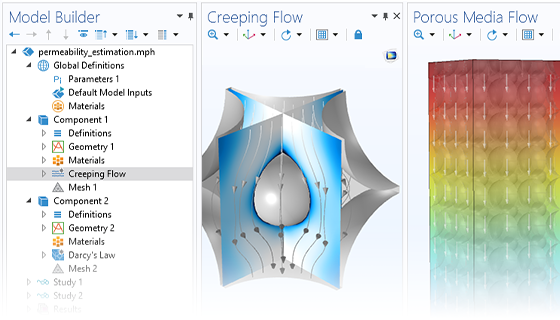
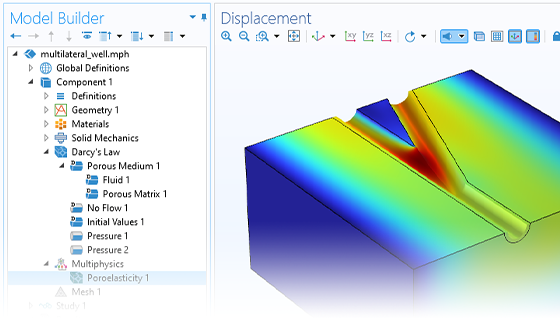
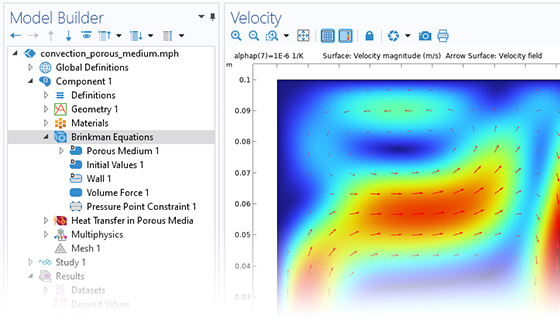
地下水流は多くの地球物理特性に影響を与える
高度な多孔質媒体モデリングの必要性は, 多くの業界とアプリケーションに及びます. 地下水流モジュールは, さまざまな業界の農業, 土木, 環境のエンジニアや科学者が地下の流れを解析し, その設計とプロセスを最適化するのに役立ちます.
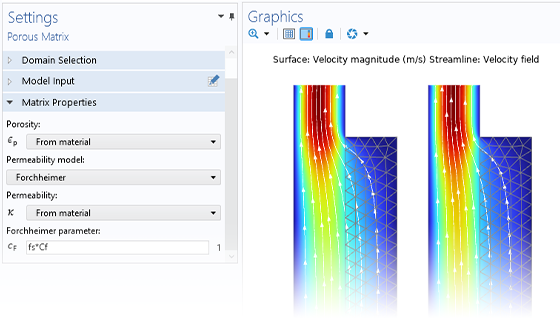
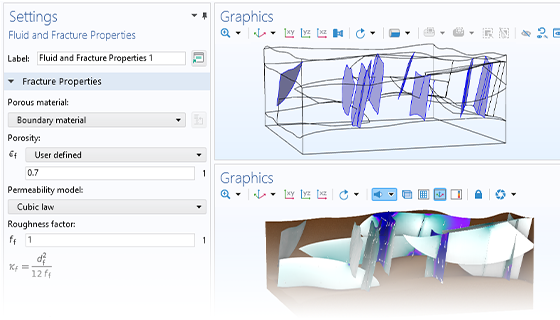
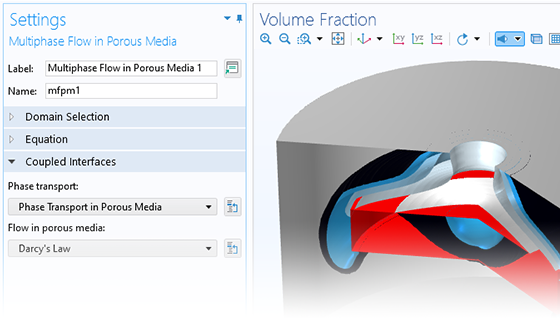
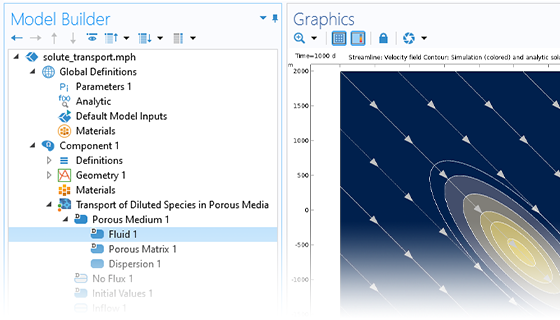
COMSOL Multiphysics® を使用すると, 多孔質媒体が水文学, 地盤工学アプリケーション, 貯留層工学, および環境工学の輸送プロセスに与える影響をシミュレートできます. このソフトウェアは, モデル化されている地下の多孔質媒体の流れのタイプに固有の方程式を自動的に設定して解く包括的なモデリング機能を提供します.