さまざまな産業プロセスを最適化する
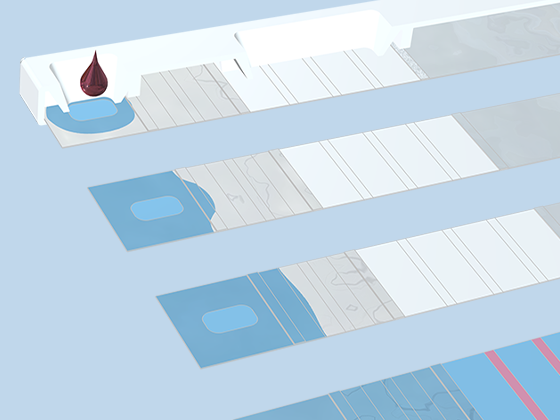
高度な多孔質媒体モデリングの必要性は, 製薬業界や食品業界など, 多くの業界やアプリケーションに及びます. 多孔質媒体流れモジュールは, さまざまな業界の農業, 化学, 土木, 原子力のエンジニアや科学者が多孔質媒体の流れを解析し, 設計とプロセスを最適化するのに役立ちます.
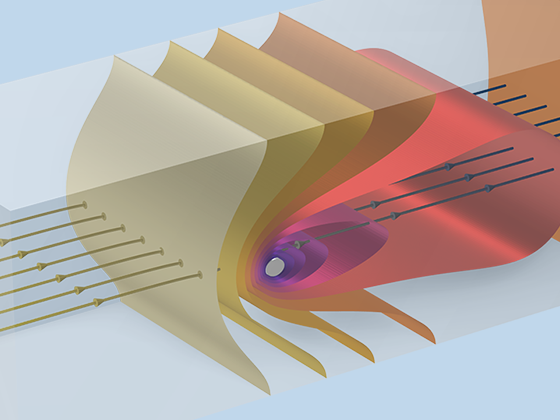
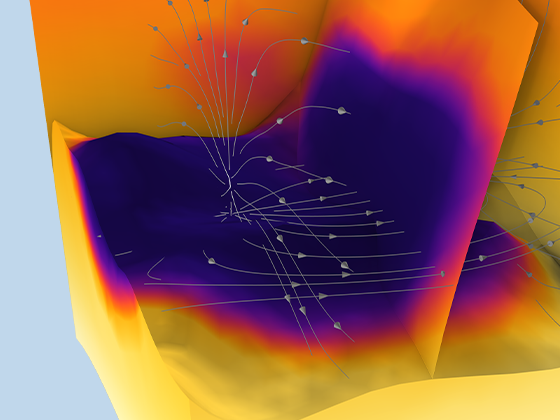
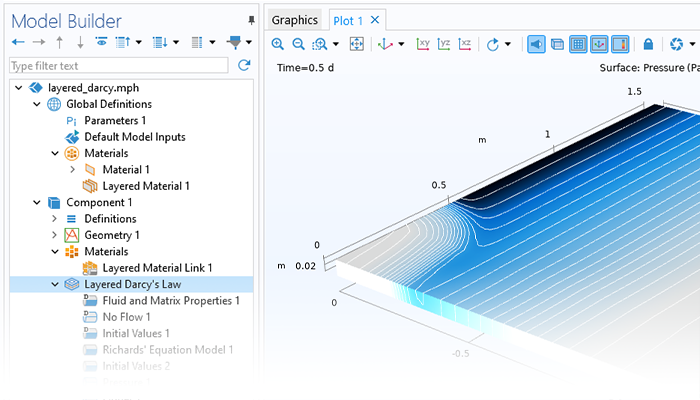
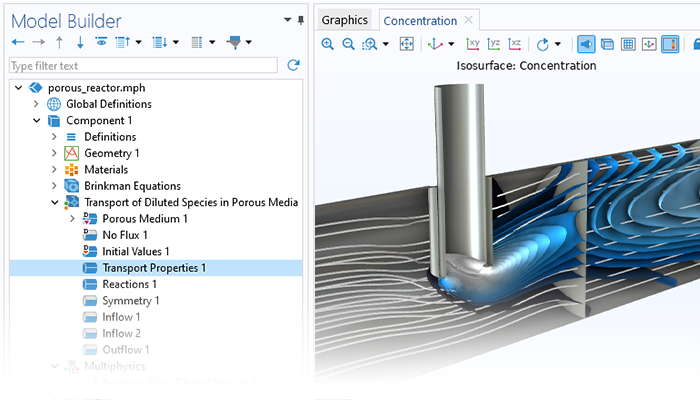
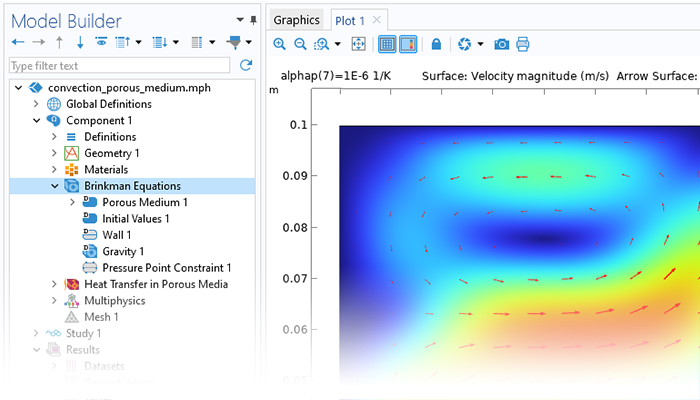
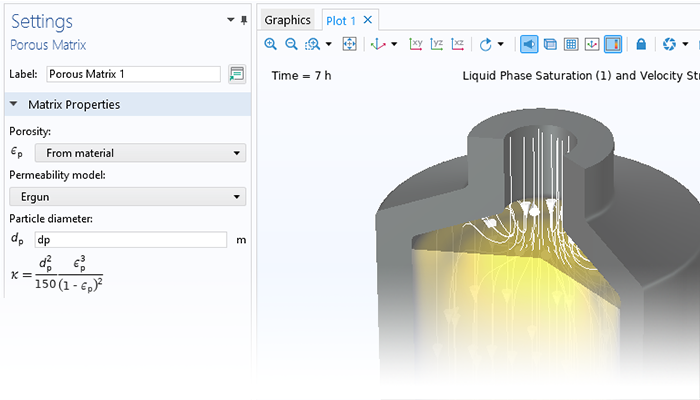
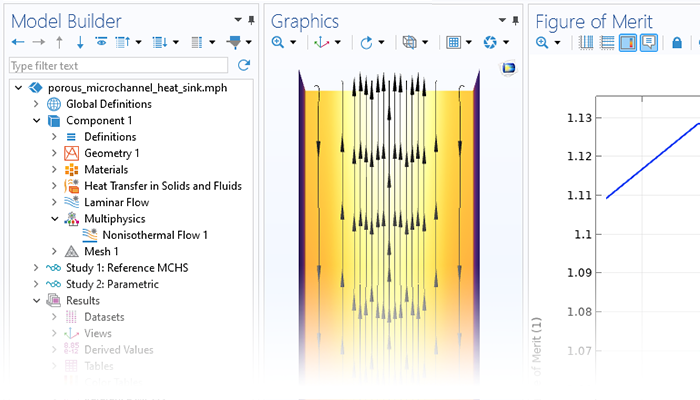
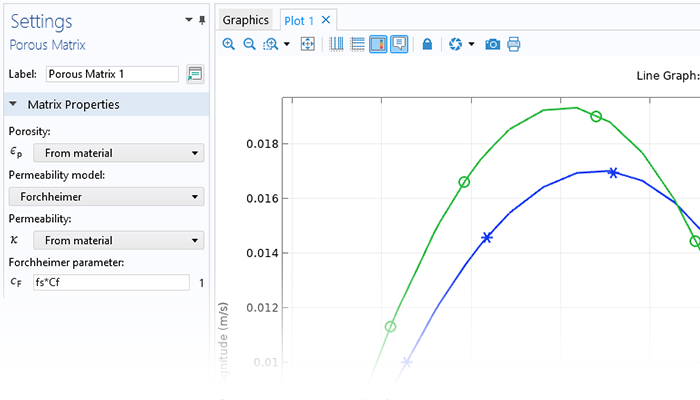
シミュレーションは, ナノマテリアル, 多孔質反応器, 電子部品の冷却, および大規模な地盤工学アプリケーションをモデル化するときに, 輸送プロセスに対する多孔質媒体の影響をキャプチャするために使用できます. COMSOL Multiphysics® は, フィジックスインターフェースにパッケージ化された包括的なモデリングツールのセットを提供します.これらのツールは, モデリングする多孔質媒体の流れのタイプに固有の方程式を自動的に設定して解きます.